【中学2年数学(確率)】確率が解けるようになるための5つのコツ


- 中学数学の確率単元が苦手なので、どうやったら苦手じゃなくなるかを知りたい
- 確率の問題を解くときのコツを知って、今よりもレベルアップしたい
このページでは、
「中学2年生で習う確率の問題を解くコツ」
を紹介していきます。
ここで紹介するコツは全部で5つ!
すべて重要ですが、その中でも重要な順番に紹介していきます。
ですので、全部は一気にできなくても、上から順番に一つずつできるようになっていきましょう。
徐々に確率の問題が解けていくようになりますよ!
中学数学の確率の問題を解くための5つのコツ
では、いきなりですが、中学数学の確率の問題を解くためのコツを発表しましょう。
- 第1位:樹形図(じゅけいず)を描けるようになる!
- 第2位:「区別する」が基本!
- 第3位:自分の感覚と相談!
- 第4位:テストに出る常連(じょうれん)さんを覚えておく!
- 第5位:「少なくとも」は、「そうでない場合」を考える!
です!
重要度ランキング第1位から5位まであります。
上のランキングでは、よくわからない表現もあるかも知れませんが、このあとで一つ一つについて丁寧に説明していきますので、安心してくださいね。
では、第1位「樹形図(じゅけいず)を描けるようになる!」から解説に入っていきましょう。
スポンサーリンク
コツ① 樹形図(じゅけいず)を描けるようになる!
第1位は、
樹形図を描けるようになる!
です。
これはダントツの一位です。
中学の確率は、これが描けるだけで8割程度の問題が解けるようになります。
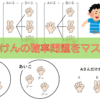
樹形図は聞いたことがありますか?下の図のようなものです↓
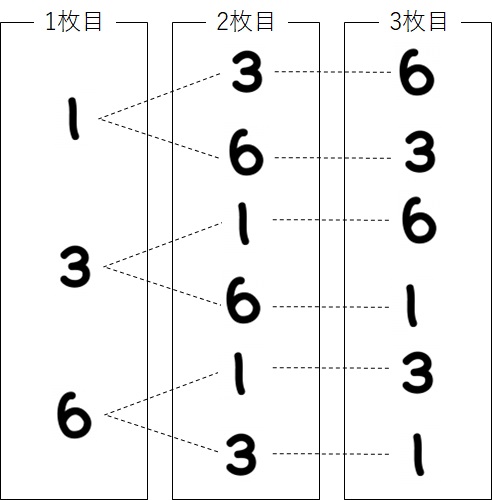
「樹形図って何?」という人は、まず樹形図を以下のページで勉強して戻ってきてくださいね↓
中学の確率の問題は、樹形図を描いて解く問題が8割以上を占めています。
なので、樹形図を正しく描ける人は、大抵の問題は解くことができます。
「樹形図なんて簡単に描けるよ」という人もいるかもしれません。
しかし、ただ描けるだけではダメです!
どんな問題でも、間違えずに正確に描ける
ということが重要なんです。
みなさんは、どんな複雑な問題でも間違えずに樹形図を描ける自身がありますか?
間違えずに樹形図を描くコツは、
「自分なりのルールを決めて、それを守って描いていく」
ことです。
どうゆうことかを少し確認しておきましょう。
例えば、以下のような問題があったとします。
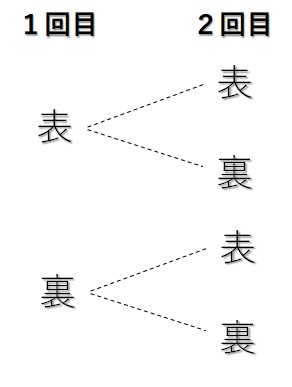
コインを二回投げて、二回とも裏となる確率を求めよ。

これに対して、問題を解くための樹形図を描いてみてください。
それは、以下のようになりますね。
だいたいの人が描けたのではないでしょうか。しかし、描けただけでは十分ではありません。
描くときに、「きちんと自分の中でルールを決めて描けたか」が重要なのです。
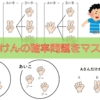
例えば、以下はよくない例です。
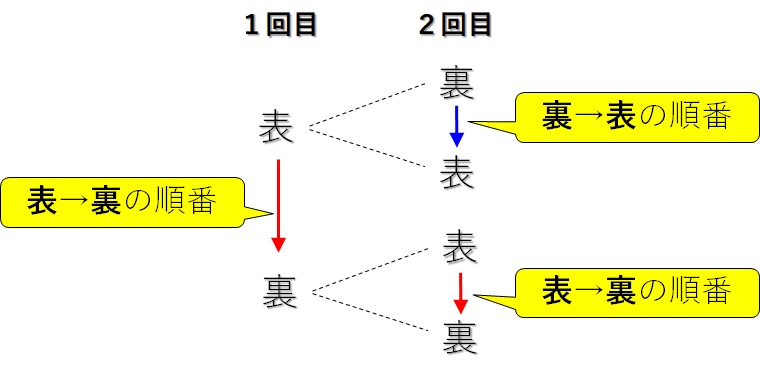
どこが良くないか分かりますか?
それは、1回目では表→裏の順番で並べていますが、2回目の上では裏→表の順番になっていますね。
これは、自分の中でルールを決めれていない証拠です。自分の中で、
(どちらも書けるときは)表から書く
と決めていれば、ある場所だけ裏から書き始めることはありません。
しっかりをルールを決めて樹形図を描くことでミスが減ります。

「そんなことしなくてもミスしないよ」という人もいるかもしれません。
確かにここで出した例題は簡単なのでミスはしないかもしれませんね。しかし、問題が複雑になってくると必ず頭が混乱してきます。
そんなとき、ルールを決めておくことが非常に大切になってくるのです。
ちなみに、ここでは「表から書く」とルールを決めましたが、必ず表から書けと言っているわけではありません。
裏から書く方が自分にはわかりやすいと思えば、「裏から書く」とルールを決めればよいです。
ただし、そう決めたのであれば必ず最後までそれを守って描くようにしましょう。
どうですか?「ルールを決めて描く」はできていますか?
ここまで読んで、「どういうこと?」って思った人や「樹形図を学びなおしたい!」という人は、以下のページから樹形図をマスターしましょう↓
もう一度言いますが、「樹形図を描ける」は重要度ダントツのナンバー1です。
これができるようになってから、次のコツに進みましょう。
② 「区別する」が基本!
二番目のコツは、
「常に区別して考える」
です。
どういうことか例題を紹介して説明しましょう。
次の例題を解いてみます。
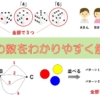
2枚のコインを同時に投げたとき、両方とも表になる確率を求めよ。

ちょっと解いてみましょう。
コインには表と裏があって、コインを投げたら、
- 表ー表
- 表ー裏
- 裏ー裏
のうちのどれかになる。
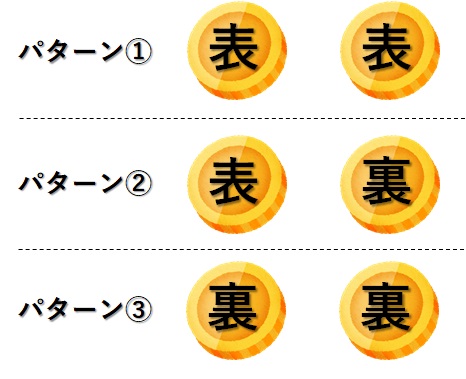
全部の組み合わせは3つで、そのうち1つが「表ー表」なので、
$$\text{両方とも表になる確率} = \frac{1}{3}$$
である。
…………このように考えた人…間違いです!
この考え方はまさに「区別をしていない」考え方になってしまっています。
パターン②に注目してください。
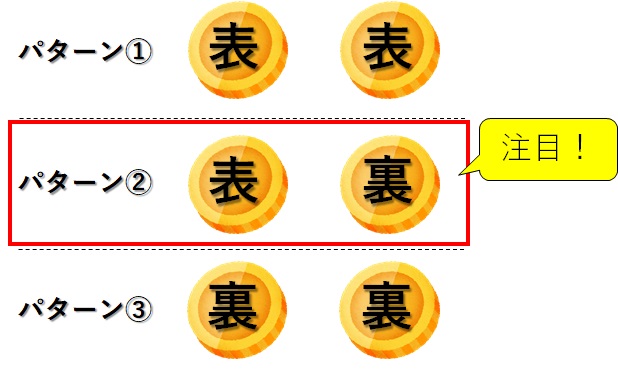
これは、表と裏が一枚ずつでるパターンです。
例えば、コインに名前を付けて、AとBとしましょう。
このようにした場合、AとBでどちらのコインが裏(もしくは表)なのかわかりません。
これが「区別していない」状態ということです。
これを「区別して」と解くには、表と裏が一枚ずつでるパターンを
- Aが表で、Bが裏のとき
- Bが表で、Aが裏のとき
を別のパターンとして考えます。
よって、パターンの数は、
- Aが表、Bも裏
- Aが表、Bは裏
- Aが裏、Bは表
- Aが裏、Bも裏
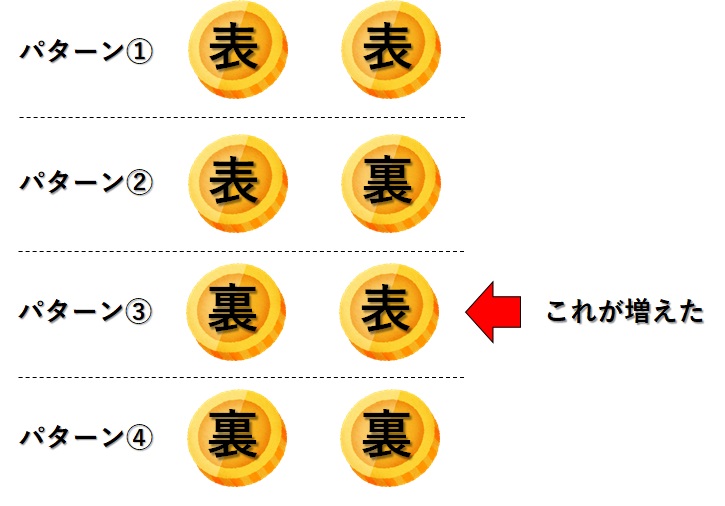
の4パターンとなります。
例題を思い出してみると、コインが両方とも表の確率を求める問題でした。
よって、全部の組み合わせは4つで、そのうち1つが「表ー表」なので、
$$\text{両方とも表になる確率} = \frac{1}{4}$$
となり、これが正しい答えです。
ここで、
- 「どのような場合に”区別して”、どのような場合に”区別しない”の?」
- 「問題によって、解き方を使い分けるの?」
と疑問に思った人もいるかもしれません。
それに対する答えは、
「常に”区別して”解け」
です。どんな問題も、どんな時も”区別した”解き方をしましょう。
中学の数学の確率問題はそれで95%以上が正解となります。
「区別する」解き方について、詳しく知りたい方は、以下の記事がオススメです↓
スポンサーリンク
③ 自分の感覚と相談!
第3位は、「自分の感覚と相談」です。
「どいうこと???」となったかもしれませんが、これは簡単なことです。以下の文章を見てください。
「サイコロを5個ふったとき、5個すべてのサイコロの目が”一(いち)”となる確率は50%です」

この文を読んだときに、「そんなわけあるか!」と思ったでしょう。サイコロ5個がすべて”一の目”が出る確率なんで、ものすごく低いはずです。
このように、明らかにおかしい文章に違和感を感じることが大切だと言いたかったんです。
「そんなこと言われなくてもやってるよ」という人がいるかもしれません。
確かに、通常の状態であれば、その違和感に気づくのは簡単です。
しかし、テスト中など時間に追われているときには、文章を単なる問題としか捉えておらず、文章の意味まで考えられなくなってしまうことは珍しくありません。
そこで、一度冷静になってください。問題を1問解き終えたら、自分の答えを見て、
「この問題文と自分が出した確率は、感覚的にありえそうか?」
と考えるのです。

これは、検算(けんざん)の一種です。
検算とは、「その計算が合っているかどうかをチェックすること」ですね。
アバウトな検算方法ですが、やってみるとかなり効果的で、しかもチェックは一瞬です。自分の感覚と合っているかを考えるだけですから。
ぜひ、この「自分の感覚と相談」するクセを身に着けましょう!
では、以下の確率についての文について、正しいかどうかを、自分の感覚でチェックする練習をしてみましょう。
- コインを5回投げて、5回とも表が出る確率は\(\frac{1}{3}\)である
- サイコロを2個投げてゾロ目が出る確率は約\(\frac{1}{6}\)%である
一つ目は間違いですね。コインを5回投げて表が連続して出る確率が\(\frac{1}{3}\)、つまり約\(30\)%のはずがありません。
二つ目は正解です。2個のサイコロ投げてどちらも同じ目になるのは、そのくらいの確率です。正確な値はきちんと計算しないとわかりませんが、しかし、明らかに間違いではなさそうだという判断はできます。
では、少し引っかけ問題ですが、
「30人のクラスで誕生日が同じペアがいる確率は約70%である」
はどうでしょうか?

実はこれ…正解です。
初めて見た人はもっと小さな確率と思ったのではないでしょうか?
これは「確率のパラドックス」と呼ばれるもので、自分の感覚が真実とは大きく違ったいように感じる現象です。
このように、自分の直感が信じれないときもありますが、これは稀です。まずは自分の感覚を信用しましょう。
余談ですが、確率のパラドックスについて詳しく知りたい人は、以下の記事をご覧ください。
※これを知っていたからといって、テストの点数は上がりませんのでご了承ください(笑)
④ テストに出る常連(じょうれん)さんを覚えておく!
テストで出題される確率の問題には、大抵決まったものが登場します。その例として、
- サイコロ
- くじ引き
- コイン
- じゃんけん
- カード(トランプなど)
- 玉(赤玉・白玉など色が付いたものや、数字が付いたものもある)

とこんなところでしょう。
登場する頻度が高いものを、ここでは「常連(じょうれん)」と呼んでいます。
このようないつも確率の問題に出てくる常連に対しては、
「基本的な組み合わせの数を覚えておく」
ことが役に立ちます。
例えば、サイコロが登場する問題で、
「サイコロを二回振りました…」
というフレーズが登場したとします。
このとき、頭に「36」という数字が思い浮かんだ人は合格です。
\(36\)という数字は、サイコロを二回振ったときのすべての組み合わせの数ですよね?↓
$$\text{1つのサイコロの目の数} \times \text{1つのサイコロの目の数} = 6 \times 6 = 36$$
この\(36\)という数字を覚えておくことで、確率を求めるときには、
$$\text{求めたい確率} = \frac{\text{〇}}{36}$$
の〇の部分を考えるだけでよいのです。
他にもいくつか例を出しましょう。
例えば、
$$2, 4, 8, 16, 36, \cdots$$
はコインを\(x\)枚投げたときの、コインの出かたのすべての組み合わせの数です。左から\(1\)枚投げた場合、\(2\)枚投げた場合、、\(3\)枚投げた場合、…となっています。
| 投げるコインの数 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| すべての組み合わせの数 | 2 | 4 | 8 | 16 | 36 |
他には、
$$\text{2人でジャンケンする場合のすべての手の組み合わせ} = 9\text{通り}$$
$$\text{3人でジャンケンする場合のすべての手の組み合わせ} = 27\text{通り}$$
などもあります。
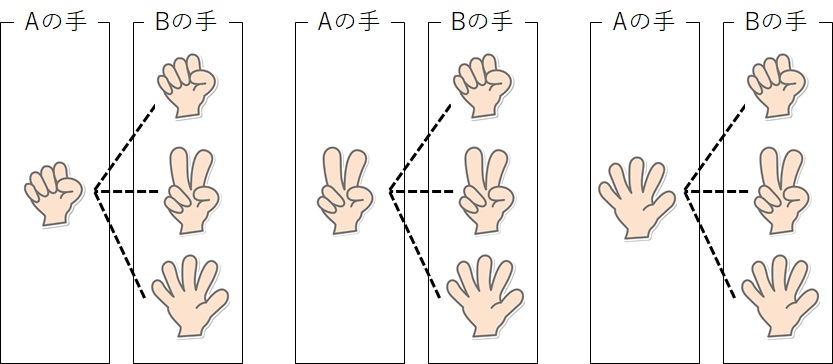
このように、よくテストに出てくるものに関しては、基本的な数については覚えておくとよいでしょう。
そのためには、多くの問題に触れておくのも大事なことです。
たくさんの問題を解いた経験があれば、テストを解いているときも、「こんな数字あのときの問題でも見たことあるなぁ、じゃあこれは合ってるはずだ。」と自信を持って回答できるようになるでしょう。
このサイトでは、テストによく出てくる常連について、一つ一つ丁寧な解説を行っています。
以下のページからいろんな常連に慣れておくようにしましょう↓
スポンサーリンク
⑤ 「少なくとも」は、「そうでない場合」を考える!
ついに、第5位です。
第4位までをクリアできた人は、最後は「少なくとも」というフレーズが登場する問題を解けるようになりましょう。
確率の問題でたびたび登場するフレーズですね。例えば次の例題のような問題をみたことがありませんか?
コインを4回投げて少なくとも1枚が表になる確率を求めよ。
この問題は、「4枚のコインが、どれか1枚でも表になる確率」というふうに言い換えることもできます。
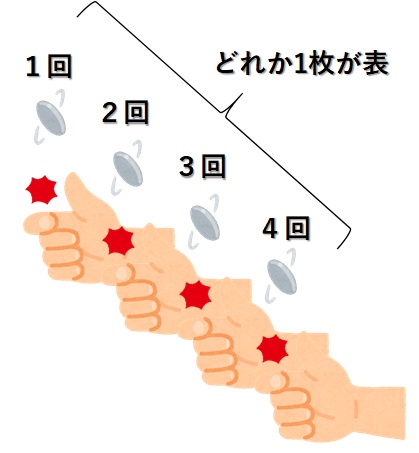
これをまともに考えていくと、
- 1枚が表になるコインの組み合わせの数
- 2枚が表になるコインの組み合わせの数
- 3枚が表になるコインの組み合わせの数
- 4枚が表になるコインの組み合わせの数
を数えなくてはいけません。
できなくはないですが、やる前から大変な作業になることは想像できますね。
ここで、
「少なくとも」は、そうでない場合を考える
というテクニックが使えます。
そうでない場合というのは、いま問題が「少なくとも1枚は表」となっていますので、そうでない場合というのは、「1枚も表がない場合」を考えるのです。
これは、真逆を考えていることになります↓
「少なくとも1枚は表」 ← 真逆 → 「1枚も表がない場合」
「1枚も表がない場合」というのは、言い換えれば「すべてが裏の場合」です↓
「1枚も表がない場合」 = 「すべてが裏の場合」
すべてが裏の場合の組み合わせの数は、すぐにわかり1つですよね。
よって、「1枚も表がない場合」の確率は、すべての組み合わせの数が\(16\)ですので、
$$\text{1枚も表がない場合} = \frac{1}{16}$$
となります。
ここで、先ほど述べたように、「1枚も表がない場合」の真逆は、「少なくとも1枚は表」ですので、この\(\frac{1}{16}\)を\(1\)から引けば、
$$\text{少なくとも1枚は表の確率} = 1 – \frac{1}{16} = \frac{15}{16}$$
となります。よって、\(\frac{15}{16}\)が例題の答えとなります。
ここでは速足で説明しましたので細かいところが分からなかったかもしれません。
しかし、まともに考えたら面倒な「少なくとも」の問題が、その逆を考えることで簡単に解けるようになることはイメージできたのではないでしょうか?
「少なくとも」が登場する確率の問題の解き方については、以下のページで詳しく解説していますので、参考にしてください↓
まとめ
ここでは、確率の問題を解くための5つのコツを紹介しました。それは、
- 第1位:樹形図(じゅけいず)を描けるようになる!
- 第2位:「区別する」が基本!
- 第3位:自分の感覚と相談!
- 第4位:テストに出る常連(じょうれん)さんを覚えておく!
- 第5位:「少なくとも」は、「そうでない場合」を考える!
でしたね。
重要度で順位付けをしていますので、第1位から徐々に第5位に向かってマスターしていくようにしましょう。
特に、第1位の樹形図は、中学数学の確率の問題を解く上で、基本中の基本ですが、これがきちんとできば8割がた問題は解けるようになります!ここは絶対に押さえておくようにしましょう。





























ディスカッション
コメント一覧
まだ、コメントがありません