【中学2年数学（確率）】カードが登場する確率の問題の解き方

2020年3月1日

はじめに知っておくべき確率問題を解くコツ

まず、はじめに確率の問題を解くために絶対に覚えておくべきコツから説明します。

これは、カードが登場する問題だけではなく、中学で登場する確率の問題すべてに対して言えることです。

 

そのコツとは、

です。

樹形図は覚えていますか？これは必ず授業で習う「確率」や「組み合わせ」の問題を解くための便利な方法です。

下の図のようなものが樹形図と呼ばれるものでしたね↓

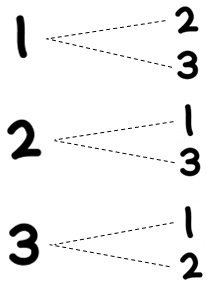
忘れてしまった人は、まずは以下の記事から勉強しましょう。樹形図について、わかりやすく丁寧に解説しています↓

 

樹形図はどんな問題でも必ず使えるものですし、正しい方法で行えばミスする可能性もすごく少ない解き方です。

しかし、たまに問題が難しくなってきたり、少し特殊な問題になってくると、樹形図を描いていると、とても時間がかかってしまう場合があります。そんなときだけ、他の工夫した方法を使うようにしましょう。

繰り返しますが、確率の問題はまずは樹形図で解こうとしてください。

 

スポンサーリンク

カードが登場する確率の問題にチャレンジ

では、カードが登場する確率の問題を解いていきましょう。

まずは、基本の問題からはじめます。以下の問題を解いてみましょう。

色々な解き方があるのですが、ここでは

• 樹形図を使った解き方
• 表を使った解き方

2つの方法を紹介します。

 

樹形図を使った解き方

まずは、樹形図を使った解き方です。樹形図を描くには、まず番号を並べるスペースを準備するのでしたね。

いまの問題は、2枚のカードを引くのですから下の図のように二つのスペースを準備します。

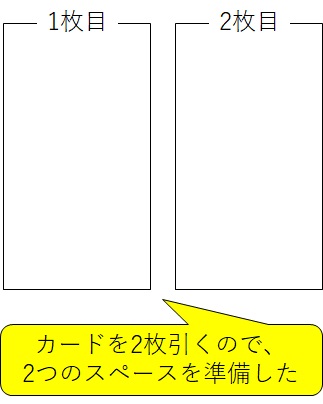
では、連続してカード引いたとき、1枚目に引く可能性のカードの番号はなんでしょうか？

カードは「1」,「2」,「3」の三枚ですから、この中の番号のカードはどれでも引く可能性があります。よって、樹形図には、

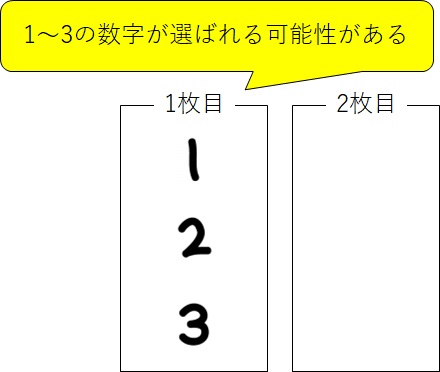
と書きます。

 

続いて、2枚目を考えていきましょう。

1枚目で「1」のカードを引いたとき、2枚目で引く可能性のあるカードの番号はなんでしょうか？

「1」はすでに1枚目で引いているのですから、2枚目で引く可能性はありません。したがって、2枚目で引く可能性があるのは、「2」か「3」です。樹形図に描くと、

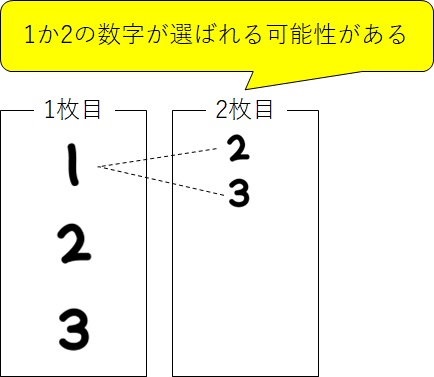
です。

同じように、

• 1枚目で「2」を引いたとき、引く可能性のあるカードの番号は「1」か「3」
• 1枚目で「3」を引いたとき、引く可能性のあるカードの番号は「1」か「2」

ですので、これも樹形図に追加しましょう↓

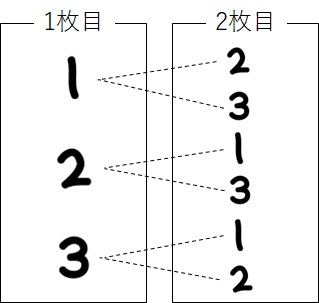
これで、樹形図の完成です。

カードの引き方は全部で6パターンあるようですね。

 

さて、例題の問題文を思い出してみると、求められているのは、

「引いた2つのカードの番号の和が3となる確率」

でしたので、作った樹形図に2つのカード番号の和を描いていきます。

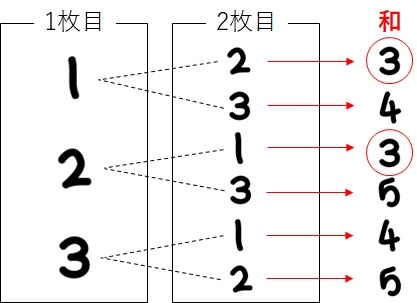
和が3であるパターン数は、2パターンですね（上図の赤丸）。

6パターン中の2パターンが和が3であるとわかったので、2枚のカードを引いたときそのようになる確率は、

$$\text{引いた2つのカードの番号の和が3となる確率} = \frac{2}{6} = \frac{1}{3}$$

となり、答えは\(\frac{1}{3}\)となります。

 

表を使った解き方

次は、表を使った解き方です。もう一度、例題を載せておきましょう↓

表は、「カードを2枚引く」ときの問題に使えます。

連続して2枚のカードを引いたときの、1枚目を表の横に書き、2枚目を表の縦に書きます↓

表の見かたは、例えばオレンジ色の★があるマスは、2枚カードを引いたときに1枚目が「3」で2枚目が「1」であることを示しています。

 

次に、このマスの中で不可能であるマスを消していきます。

例えば、下の図の青い★マークのあるマスはどうでしょうか？

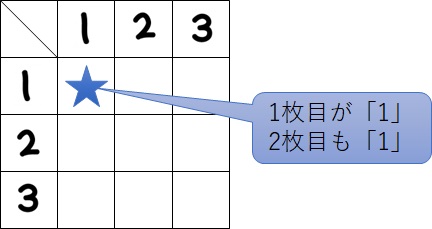
このマスが意味するところは、1枚目が「1」であり2枚目も「1」であるということです。

 

しかし、いまの問題では「2枚のカードを連続して引く」ということですので、2枚目に1枚目と同じ番号を引くことはあり得ません。

したがって、この青い★のマスは取り得ないのです。なので、そのようなマスは斜線を入れて消しましょう。

同じように、「2」と「3」についても2枚目に同じ番号にはならないため、表は下の図のようになります。

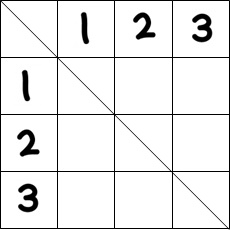
これで表は完成です。表の空きマスになっている箇所が、2枚のカードを引いたときに取りうるすべてのパターンということになります。

空きマスの数を数えると、全部で6マスありますね。つまり、2枚のカードを引いたときに取りうるすべてのパターンの数は6パターンであるということになります。

 

では、「和が3になる確率」を調べましょう。まずは、表の空きマスに縦と横の数字の和を書いてみます。

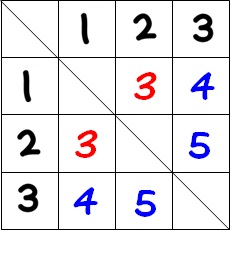
和が3になるのは、2マスですね。よって、2枚のカードを引いたとき和が3になる確率は、

$$\text{引いた2つのカードの番号の和が3となる確率} = \frac{2}{6} = \frac{1}{3}$$

となり、答えは\(\frac{1}{3}\)となります。

当然、樹形図を使って解いたときと答えは同じになります。ならなければいけません。

 

小まとめ・表を使って解くときの注意点

ここでは、「樹形図を使った方法」と「表を使った方法」を紹介しました。

個人的には、この問題に限っては表を使った解き方のほうが、わかりやすくて早いのかなと思いますが、はじめにも述べたように中学数学の確率の問題を解く基本は「樹形図」です。

確率の問題をあまり解いたことがない人は、どんな問題もまずは樹形図を使って解くと決めておいてもいいと思います。

 

話は変わりますが、表を使って解くときの注意すべき点を述べておきます。

それは、

「カードを2枚引くときにしか使えない」

ということです。

表は、横に1枚目のカード番号を、縦に2枚目のカード番号を書きます↓

では、問題が「3枚のカードを引く」というものであったらどうでしょうか？

もう3枚目に引いたカードの番号を書く方法がありませんね。

なので、表は引くカードが2枚までしか対応していないのです。

 

一方、樹形図であれば「3枚のカードを引く」場合にも対応可能です。その場合、イメージですが下の図のように書けばいいのです。

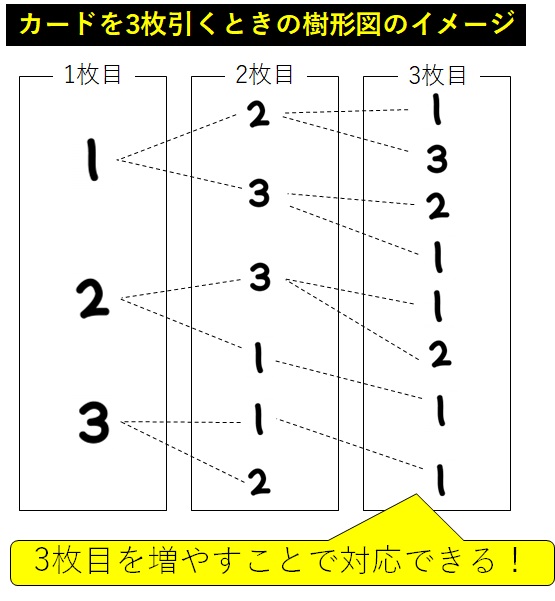
※この樹形図はあくまでイメージであり、数字の配置や点線の結合などは問題によって変わってきます。

 

少しだけ難易度を上げた問題に挑戦しよう

もう一問だけカードが登場する確率の問題を解いてみましょう。

今度は、少しだけ難易度が上がります。

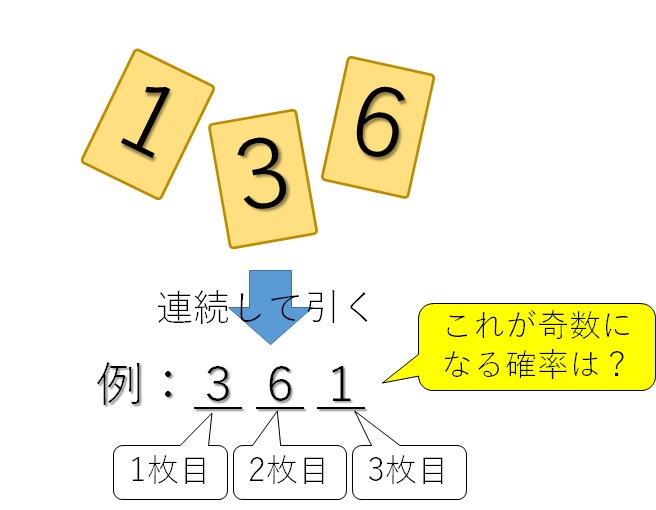
この問題は3枚のカードを引くため、表を使用する解き方では解けません。

よって、樹形図を使って解いていきます。

樹形図を描いていきましょう。まずは、3枚分のスペースを用意します。

 

まず、1枚目に「1」を引いたとします。すると、2枚目は「3」か「6」です。

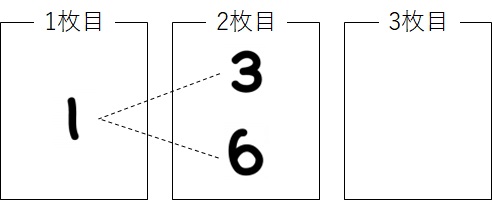
2枚目に「3」を選んだときは、残りの一枚である「6」が3枚目に選ばれます。一方、2枚目に「6」を選んだときは、残りの一枚である「3」が3枚目に選ばれます。

それを、樹形図に追加すると、

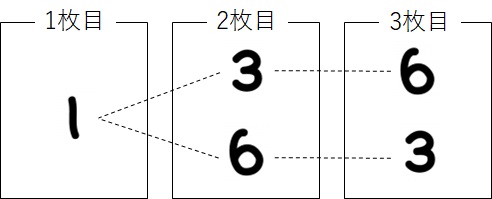
と描けます。

 

同じように、1枚目に「3」や「6」を選んだ場合についても樹形図に描き加えると、

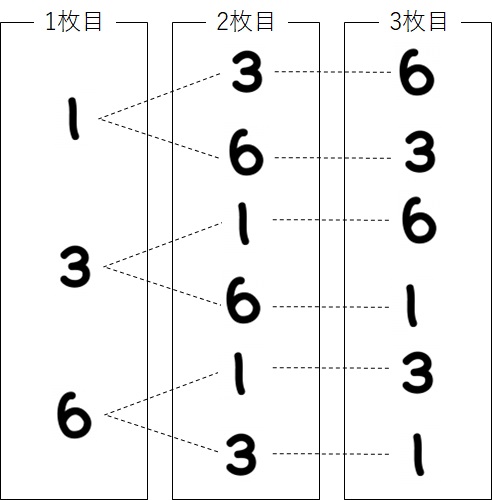
となります。これで、樹形図は完成です。全部で６パターンの取り出し方があることがわかりましたね。

 

さて、例題で求められていることは、

「1枚目を百の位、2枚目を十の位、3枚目を一の位として3桁の数にしたときに奇数となる確率は？」

でしたので、まずは3桁の数を樹形図の右に書いてみます。

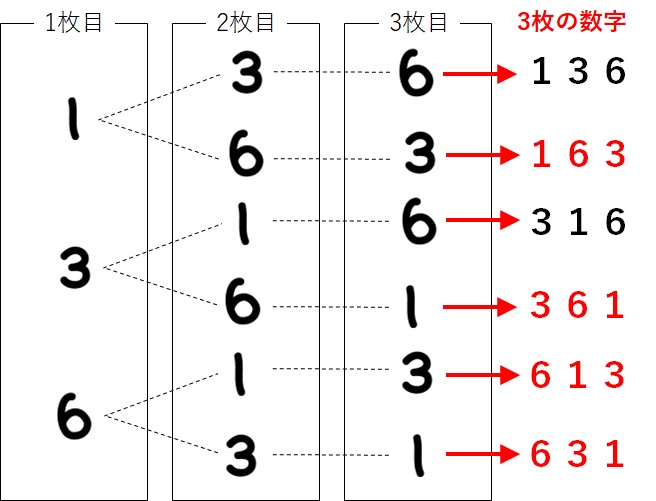
この6つの数字の中で、奇数の数を数えると、上の図の赤い数字になります。すなわち4パターンですね。

 

よって、「１」「３」「６」のカードから3枚を連続で取り出し、3桁の数字にしたときに奇数となる確率は、

$$\frac{4}{6} = \frac{2}{3}$$

となり、答えは\(\frac{2}{3}\)ということになります。

 

スポンサーリンク

まとめ

ここでは、カードを使った確率の問題を2問だけ紹介して、その解き方を丁寧に解説しました。

ここでの解き方がカードが登場する問題を解くときの基礎の基礎になります。しっかりとマスターしましょう。

 

問題へのアプローチとしては、まずは「樹形図」を使って考えてみることです。

問題をたくさん解いて慣れてきたら、表での解き方も知っておきましょう。

表で解いた方が手間がかからない場合が多いので、表が使えそうなときは積極的に使っていっていください。

 

以下のページにカードだけではなく、色々な確率の問題を攻略するための学習プログラムを用意しています↓そちらも参考にしてみてください。