数独の解き方【超上級編③】「XY-wing（エックスワイ・ウィング）」法
XY-wing法（エックスワイ・ウィング）法というある条件を満たす三つのマスを見つけて、その周辺のマスの数字の候補を絞る方法を紹介します。
超上級編の最後に紹介するにふさわしい、上級テクニックとなっています。
X-wing法に名前が似ているけれど解き筋はまったく違う「XY-wing法」
ここでは、数独の解き方の中級編で紹介した「X-wing（エックス・ウィング）法」に名前が似ているけれど解き筋はまったく違う「XY-wing法」という手筋を紹介します。
XY-wing法には、２つのパターンがあるので、それぞれ解説していきます。
スポンサーリンク
パターン１
まずは【パターン１】の解説です。
今、３つのマスＡ・Ｂ・Ｃについて、次の状態になっているとします。
- マスＡには１と２のみが入り得る。
- マスＢには１と３のみが入り得る。
- マスＣには２と３のみが入り得る。
- マスＡとＢは同じ列上にある（ただし、同じブロック内にはない）。
- マスＡとＣは同じ列上にある（ただし、同じブロック内にはない）。
- マスＡ・Ｂ・Ｃは一直線上にない。
「あ〜もうっ！条件が多すぎて非常にわかりにく〜いっ！」
なので、下図を見てビジュアル的に理解しちゃってください。
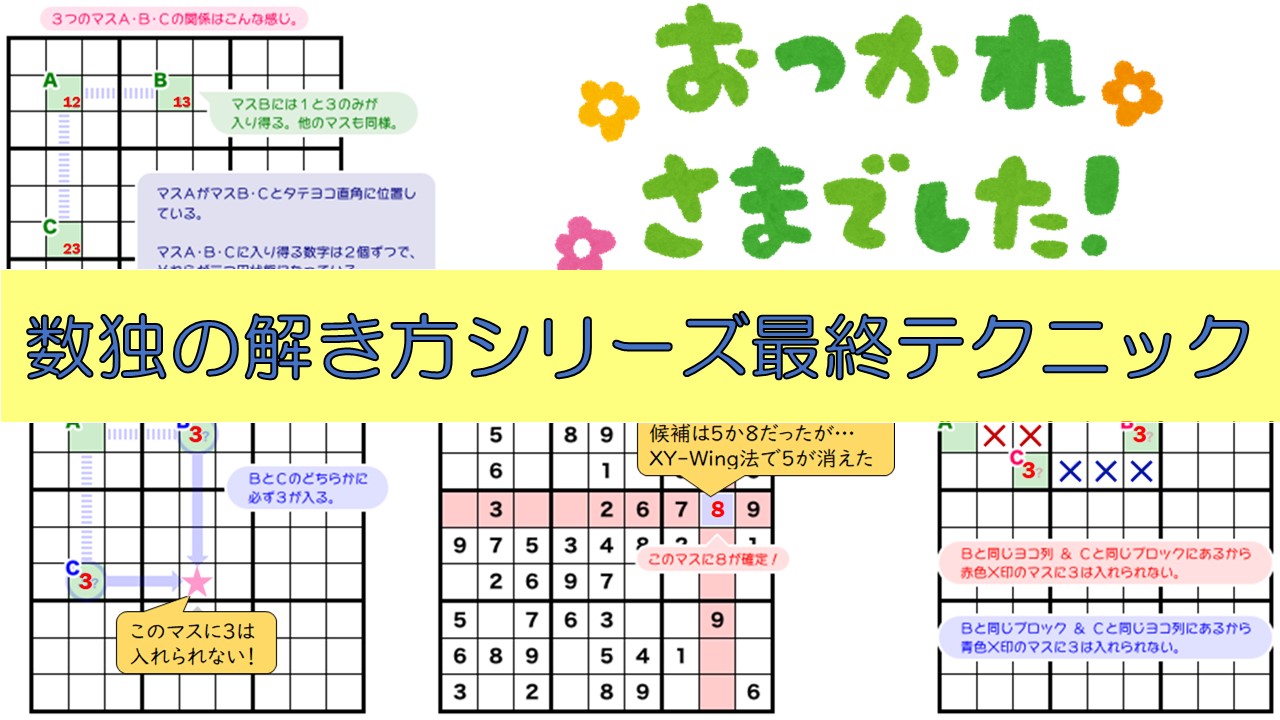
マスＡがマスＢ・Ｃとタテヨコ直角に位置していて、マスＡ・Ｂ・Ｃに入り得る数字が２個ずつあってそれらが三つ巴状態になっている、といったイメージです（三つ巴とは、上図の 12，13，23 のことです）。
この状況になった時、★マス（下図）に注目してみましょう（実は、★マスもマスＢ・Ｃとタテヨコ直角に位置しています）。
この状態で、どういうことが成り立つのか……。
マスＡには１と２のどちらかが必ず入るので、その数字を入れるとマスＢ・Ｃのどちらかに影響が出ます。
マスＡに１が入った場合、マスＢには３しか入れられません。
マスＡに２が入った場合、マスＣには３しか入れられません。
どちらにしても「マスＢ・Ｃのどちらかに必ず３が入る」ということが言えます。
したがって、★マス（下図）には３を入れることができないわけです。
これが【パターン１】の手筋です。
マスＢ・Ｃに入り得る数字を見てみると、「３」が共通しています。
その数字「３」が★マスに入らないことが判明しました。「マスＢ・Ｃに共通する数字が★マスに入らない」と覚えると手っ取り早いでしょうか。
実例で解き方を見てみよう
【パターン１】の説明が終わったところで、実例を挙げてみましょう。下図の緑色の３マスに入り得る数字をそれぞれ調べてみます。
すると、この３マスに入り得る数字は各２個ずつで、さらに１・５・７の三つ巴！（下図）これはもう XY-wing法の出番です！
★マスに注目しましょう！
XY-wing法の手筋を使うと、「マスＢ・Ｃのどちらかに必ず５が入る」ということがわかります。
そのため、★マス（下図）に５を入れることができません。
★マスを含むタテヨコの列（下図の赤色）を見てみると、５と８以外の数字がすでに入っています。
そして、XY-wing法によって★マスに５が入らないことはもうわかっています。
というわけで、８しか入らないということがわかるわけです。
パターン２
次は、【パターン２】の解説です。
今度は、３つのマスＡ・Ｂ・Ｃについて、次の状態になっているとします。
- マスＡには１と２のみが入り得る。
- マスＢには１と３のみが入り得る。
- マスＣには２と３のみが入り得る。
- マスＡとＢは同じ列上にある（ただし、同じブロック内にはない）。
- マスＡとＣは同じブロック内にある（同じ列上にあるかどうかは問わない）。
- マスＡ・Ｂ・Ｃは一直線上にない。
【パターン１】とは５番目の条件が異なるだけなので、やっぱりこれも条件が多い〜！
下図を見て、またビジュアル的に理解しちゃってください。
マスＡと列を共有しているマスＢ、マスＡとブロックを共有しているマスＣ。
マスＡ・Ｂ・Ｃに入り得る数字が２個ずつあってそれらが三つ巴状態。
そんなイメージです（三つ巴とは、上図の 12，13，23 のことです）。
この状況になった時、どういうことが成り立つのか……。
マスＡには１と２のどちらかが必ず入るので、その数字を入れるとマスＢ・Ｃのどちらかに影響が出ます。
マスＡに１が入った場合、マスＢには３しか入れられません。
マスＡに２が入った場合、マスＣには３しか入れられません。
どちらにしても「マスＢ・Ｃのどちらかに必ず３が入る」ということが言えます。
そうなると、３を入れられないマスが生じます。
✖印の５マス（下図）です。
赤色の✖マスは、Ｂと同じヨコ列かつＣと同じブロックに属しています。
そのため、ＢとＣのどちらに３が入っても赤色✖マスに３を入れることができません。
青色の✖マスは、Ｂと同じブロックかつＣと同じヨコ列に属しています。
そのため、同様に青色の✖マスに３を入れることができません。
これが【パターン２】の手筋です。
【パターン１】とは結論がだいぶ違いますね。
マスＢ・Ｃに入り得る数字を見てみると、「３」が共通しています。
その数字「３」が✖マスに入らないことが判明しました。
「マスＢ・Ｃに共通する数字が✖マスすべてに入らない」と覚えると手っ取り早いでしょうか。
上記ではＡとＢが同じヨコ列に属している場合の説明をしましたが、当然、ＡとＢが同じタテ列に属している場合でも同じことが成り立ちます。
例えば、３マスＡ・Ｂ・Ｃが下図のような状態の場合です。この場合も、同じ理屈により✖印の５マスに３を入れることはできません。
実例で解き方を見てみよう
【パターン２】の方も実例を挙げましょう。
下図の緑色の３マスに入り得る数字をそれぞれ調べてみます。
すると、この３マスに入り得る数字は各２個ずつで、さらに２・４・８の三つ巴！（下図）さぁ、XY-wing の出番です！
早速使いましょう！
XY-wing法の手筋を使うと、「マスＢ・Ｃのどちらかに必ず２が入る」ということがわかります。
そのため、✖印のマス（下図）に２を入れることができません。
✖印のマスに２が入らないことを踏まえつつ、緑色ブロックと赤色ヨコ列を見てみると……どちらも２が判明しちゃいました！
XY-wing法を使うためには、たくさんの空きマスに対して入り得る数字を逐一調べて、該当の３マスを見つけなければいけません。
そういう意味では、多少メンドウな手筋と言えます。
タテ列やヨコ列を見て、入り得る数字が「a, b」と「a, c」（a, b, c はとある数字）の形である２マスが見つかった時、「あ、三つ巴があるかも……」と XY-wing の手筋を意識してみると良いかもしれません。
スポンサーリンク
問題に挑戦しよう
ここでは、このサイトの数独解き方シリーズ最後の「XY-wing法（エックス・ウィング）法」を知りました。
この解き方を使って以下の問題に挑戦してみましょう！
[問題掲載予定]
まとめ
- XY-wing法は三つ巴の数字をマスを見つけて、数字の候補を絞る方法です。
- パターン１とパターン２があり、広い視野を持って使えるパターンを探す能力が必要な上級者向けのテクニックです。