6つの円周率に関する面白いこと – πに関する新発見があるかも…

円周率に関する面白いことを紹介しています。
数学的に美しいことから、ちょっとくだらないけど「へぇ~」となるトリビア的なネタまで、円周率に関する色々なことを集めてみました。
円周率\(\pi\)を簡単に復習
はじめに円周率(\(\pi\))について、ちょっとだけ復習しましょう。
円周率とは、
円の周りの長さが、円の直径に対して何倍であるか?
という値です。
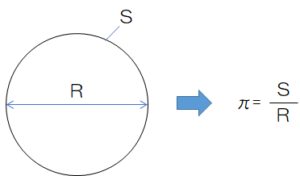
下の画像のような円があったとします。

円の直径を\(R\)、円周の長さを\(S\)とすると、”円周の長さが直径の何倍か”というのが円周率なので、
$$\pi = \frac{S}{R}$$
となります。
そして、この値は円のどんな大きさの円だろうと変わらずに、一定の値となります。その値は、
$$\pi = \frac{S}{R} = 3.141592\cdots$$
です。
これが円周率です。
この円周率には不思議で面白い性質がたくさん隠れています。
それらを以下では紹介していきましょう。
スポンサーリンク
円周率\(\pi\)の面白いこと①:\(3.14\)にはPI(E)がある
まずは、ちょっとくだらない円周率のトリビアを紹介します。
誰しも知っていることですが、円周率は英語でpiと書きますね。そして、その値は、
$$\text{pi} = 3.14\cdots$$
です。
このpiと\(3.14\)の不思議な関係を紹介しましょう。
まず、紙に\(3.14\)と書いてください。こんな感じですね↓
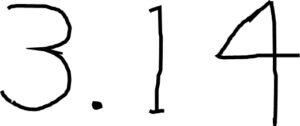
これを左右逆にしてみます。すると、
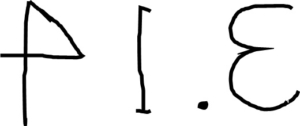
ですね。
では、この下にpie(パイ)を大文字で書いてみましょう。

なんか似ていませんか?
3.14にはパイが隠されていたのですね。
ちなみに、\(\pi\)のスペルはpiです。pieは食べ物のパイですね…

…おしい!
同じように、円周率がピザと関係しているというくだらないネタもあります。
興味がある人は下の記事を見てみてくださいね。
円周率\(\pi\)の面白いこと②:円周率をピアノで弾くと美しい
ここも数学とはあんまり関係ないことですが、私はちょっと驚きました。
”円周率をピアノで弾く”という動画を発見したのです。
しかも、それが結構いい音楽なのです。音楽には疎(うと)い私ですが感動しました。
以下がその動画です。
動画の右上に載っていますが、円周率に出てくる数字を鍵盤の各キーに割り当てて、順番どおりに弾いているのですね。
右手で円周率を弾き、左手は伴奏だそうです。
楽譜を探してきました。途中からですが下の画像が楽譜の一部です。
私は楽譜が読めないですけど、確かに円周率になっているようです。
スポンサーリンク
円周率\(\pi\)の面白いこと③:無限に続く\(\pi\)の中に隠れる不思議な数字の並びたち
円周率は無限に続く数字の並び(\(3.141592\cdots\))です。この中に、面白い数字の並びがいくつか発見されていますので、紹介しましょう。
ファインマン・ポイント
円周率の小数点以下762桁目から”\(9\)”が6回連続で現れます。
この連続した\(9\)の並びをファインマン・ポイントと言います。
ファインマンさんは有名な物理学者でノーベル物理学賞も受賞しているすごい人です。
彼が、
「この位置までの円周率を暗記したい」
と自分の講義中に言ったことが、ファインマン・ポイントと呼ばれるようになった所以(ゆえん)です。
“\(0\)”が12個連続する
現在、円周率は小数点以下の何兆桁まで計算されていますが、その中に”\(0\)”が12個連続して並ぶ箇所があることが分かりました。
ただし、そんなに驚くべきことでもなく、「何兆桁もランダムで数字を並べていれば、そんな数字の並びも出てくるだろう」ということです。
実際、確率的に考えると、2兆桁を超えるランダムな数字の並びの中では特定の数字が12回連続して並ぶことは2,3回はあるそうです。
“\(123456789\)”が登場する
円周率は無限に続く数字ですので、どんな数字も登場します。
もちろん、\(123456789\)という並びも登場しており、これは5億2355万1502桁目で初登場するそうです。
もう桁数の感覚がわからん。
“\(0\)”はなかなか登場しない
これは少し興味深いのですが、円周率をはじめから言っていくと、なかなか\(0\)が登場しないらしいのです。
実際に以下に、円周率を書いてみましょう。
$$\pi = 3.14159265358979323846264338327950288\cdots$$
3.14から見ていくと、いろんな数字がランダムに並んでいますが、\(0\)がなかなか現れません。
そして、ようやく小数点32桁目で登場します。
これは他の数字に対して、圧倒的に遅いですね。
何か意味があるのでしょうか?それとも偶然でしょうか?
円周率\(\pi\)の面白いこと④:\(\pi\)は約4000年前から使われていた
円周率の歴史はものすごく長いです。
世界で初めて円周率の研究が始まったのでは、今から約4000年前、紀元前2000年頃でした。
その当時、文明が発達していた古代バビロニアのバビロニア人とエジプト人が、建造物を建てる際、円の円周の長さを知る必要があったため円周率という概念を考え出したと言われています。
彼らは円の直径に\(3\)を掛けることで、円周の長さを求めていました。
$$\text{円周の長さ} = \text{円の直径} \times 3$$
つまり、彼らは円周率を\(3\)として計算していたのですね。
おそらく、何の数学的根拠もなく\(\pi=3\)としていたのでしょうが、それにしては正確な値を見つけていたのですね。
そして、少し時代が経過すると、さらに精度がよくなります。彼らは、
$$\pi = 3\frac{1}{8} = 3.125$$
を使い始めます。
正しい円周率の値が、\(\pi=3.141592\cdots\)ですので、かなり正確な値へ近づいてきましたね。
その後も円周率のより正確な値を求めて、数々の研究が行われてきました。
現在では、円周率は小数点以下、何兆桁まで分かっていますが、それでも正確な値ではありません。
以下の記事では、「歴史上、円周率がどのように研究されてきたのか?」「コンピュータの無い時代に、どうやってより正確な円周率を目指したのか?」という円周率の歴史について紹介しています。
スポンサーリンク
円周率\(\pi\)の面白いこと⑤:こんな実験で\(\pi\)を求めることができるの?
円周率を求めるために歴史上の偉大な数学者たちが、素晴らしい数学のアイディアを駆使してより正確な値に近づけていったことは、前述した円周率の歴史をみればわかると思います。
しかし、円周率を求める方法は、なにも数学を使った方法だけではないのです。
例えば、フランスの数学者ルクレール・ド・ビュフォンはある実験によって円周率を導く方法を提案しました。
それは、
平行な線が描かれた床の上に、針を投げる

という実験です。えらく単純な実験ですね。
このとき、投げる針の長さは、平行な線の間隔の半分の長さです。
そして、何回も何回も針を投げ続け、平行な線と投げた針が交わった回数と針を投げた回数の比をとります。
$$\frac{針を投げた回数}{平行な線と投げた針が交わった回数}$$
何回も針を投げ続けていくと、これが円周率\(\pi\)に近づいていくというのです。
$$\frac{針を投げた回数}{平行な線と投げた針が交わった回数} \rightarrow \pi$$
平行な線も針も直線的なものです。
一方、円周率とは円に関係した曲線的なものです。
なぜ、このような実験で円周率が出てくるのでしょうか?不思議ですね。
続きは、どうぞ以下の記事からご覧ください。
円周率\(\pi\)の面白いこと⑥:その他の雑学・トリビア
最後は、円周率に関する雑学・トリビアを箇条書きにして紹介していきます。
- 数学の分野でもっとも有名な定数は円周率\(\pi\)でしょう。円周率は数学のどの分野でも登場する重要で不思議な性質を持った定数です。

- 今でこそ、円周率の記号には”\(\pi\)”が使われていますが、これはほんの250年前から使われ始めた記号です。オイラーがこの記号を広めたと言われています。円周率の歴史が4000年であることを考えると短い歴史ですね。

- 現在も円周率の本当の値は分かっていません。というより”\(\pi\)の正確な数は分からない”ということが分かっています。…ということは私たちは一生、円の面積の本当の値を知ることはないでしょう。
- \(\pi\)はギリシャ語のアルファベットですが、\(\pi\)は16番目の文字です。英語でもpが16番目の文字となっています。

- 円周率は、円の円周とその直径の比を表すことは上で説明した通りです。それは、円の直径が円周の周りに回数収まるかという意味にも取ることができます。
- 3月14日は円周率の日として毎年祝われます。これは円周率の近似値\(3.14\)から来ています。円周率の日は、1988年に物理学者ラリー・ショウが祝ったのが始まりです。彼は、この日、パイをスタッフに振る舞いました。

- 円周率は無理数なので、分数で表現することはできません。歴史上の数学者は、\(\frac{22}{7}\)や\(\frac{355}{113}\)が円周率に近いことは知っていましたが、それらは正確には円周率の値ではありません。
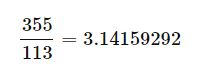
- 円周率は数字のパターンや繰り返しがありません。数字はランダムに現れます。現在、この数は小数点1兆桁以上計算され分かっています。また、中国人の呂超は67,890桁まで覚えておりこれはギネスにも認定されている世界記録です。
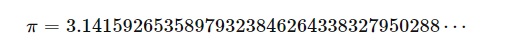
- オランダの数学者ルドルフ・ファン・コーレン(1540年1月28日 – 1610年12月31日)は人生の大半を円周率の計算に捧げた人です。彼は、コンピュータなど無い時代に円周率を36桁まで求めました。これは、コーレン数と呼ばれています。
- 19世紀になると、ウィリアム・シャンクスという人物が円周率の707桁までを手計算で求めました。しかし、残念ながら527桁目で間違っていることが後に分かります。
- 我等が日本の科学者は強力なコンピュータ”Hitachi SR 8000”を使って1兆2400億桁の\(\pi\)を計算し、これまでのすべての記録を破りました。
- \(\pi\)の359桁目には、”360″が現れます。円が360度であることと何か繋がりを感じます。
- 円周率の計算は、コンピュータの計算負荷測定に使用されています。
- \frac{104348}{33215}は\(\pi\)をもっとも正確に表現できる分数です。その精度は素晴らしく、00000001056%の誤差しかありません。
- 人間は4000年以上、円周率を研究しています。
- 円周率は聖書にも記載されている。
- アインシュタインは”円周率の日”に生まれました。
- プラトンは\(\pi\)の正確な値を\(\sqrt{2}+\sqrt{3}=3.146\)と推測していました。
- 多くの人は円には”角がない”と認識しています。しかし、”角が無限にある”という表現の方が数学的に正解です。
- 円周率の最初の6桁(\(314159\))は、1,000万桁までで6回登場します。































ディスカッション
コメント一覧
値が求められない、とは
πのことではなく
Ωのことではないでしょうか
夏休みの課題で円周率についてのレポートを書いているのですが、とてもためになる内容で、わかりやすかったです。ありがとうございました。
僕は50桁まで言えます
≪…πの面白いこと…≫は、線や面、形にそれぞれ変身できているコトだ。
線では、半円周 → π
面では、円 → π
曲面では、1/4面(みかんの有田剝きのひとつの面) → π
形では、『釣り鐘体』や『富士山体』、『カルデラ体』や『朝顔体』 → π
1は、線 正方形、正立方体 → 1 で表示できる。
πと自然数のお話は、絵本「もろはのつるぎ」(有田川町ウエブライブラリー)あり。
先日、3月14日1時59分26秒を見ました。
100桁くらいしか言えない…
僕は10000桁くらいまでしか言えない・・・
せんせー!
ここにやべー奴いまーすw!!ヽ(゚д゚ヽ)(ノ゚д゚)ノ!!
いや、スゲーよw
ピンバック & トラックバック一覧
[…] その他、もっと円周率知りたい!という方、こちらに円周率にまつわる雑学が紹介されていて、面白いですよ。見てみてくださいね。 […]