なぜ「aの0乗は1」なのか？ – その納得の理由を紹介します
中学の数学の授業で、\(a\)の\(0\)乗は\(1\)だと教わります。
$$a^0 = 1$$
「なぜ？」「\(0\)じゃないの？」と思った経験はありませんか？
ここでは、なぜ「aの\(0\)乗は\(1\)なのか」に対して、その納得の理由をいくつか紹介します。
なぜ「aの0乗は1」なのか？
中学校の数学で、累乗（るいじょう）というものを習います。
以下のようなものですね。
$$3^5$$
\(3\)を5乗しています。
これは、\(3\)を5回掛けることを意味します。
ですので、\(3^5\)を計算すると、
$$3^5 = 3 \times 3 \times 3 \times 3 \times 3 = 243$$
となります。
つまり、\(a\)の\(m\)乗、
$$a^m$$
は\(a\)を\(m\)回掛けたものと言えそうです。
では、\(m\)に\(0\)が入った
$$2^0$$
はどうでしょうか？
中学校では、
どんな数でも\(0\)乗すると、\(1\)である
と教わりませんでしたか？
ですので、\(2\)の0乗も\(1\)となります。
$$2^0 = 1$$
\(2\)の0乗ということは「\(2\)を0回掛けたもの」ということです。
「0回掛ける」ということは「何も掛けない」こととも解釈できます。
なぜそれが\(1\)になるのでしょうか？
\(2^0=0\)となってくれた方がまだ納得できる気もしますよね。
さて、ここでは0乗が\(1\)になる理由について、最後には必ず納得してもらえる説明をいくつか紹介します。
みなさんはどの説明が一番好きですか？
スポンサーリンク
規則性から0乗が1であることを知る
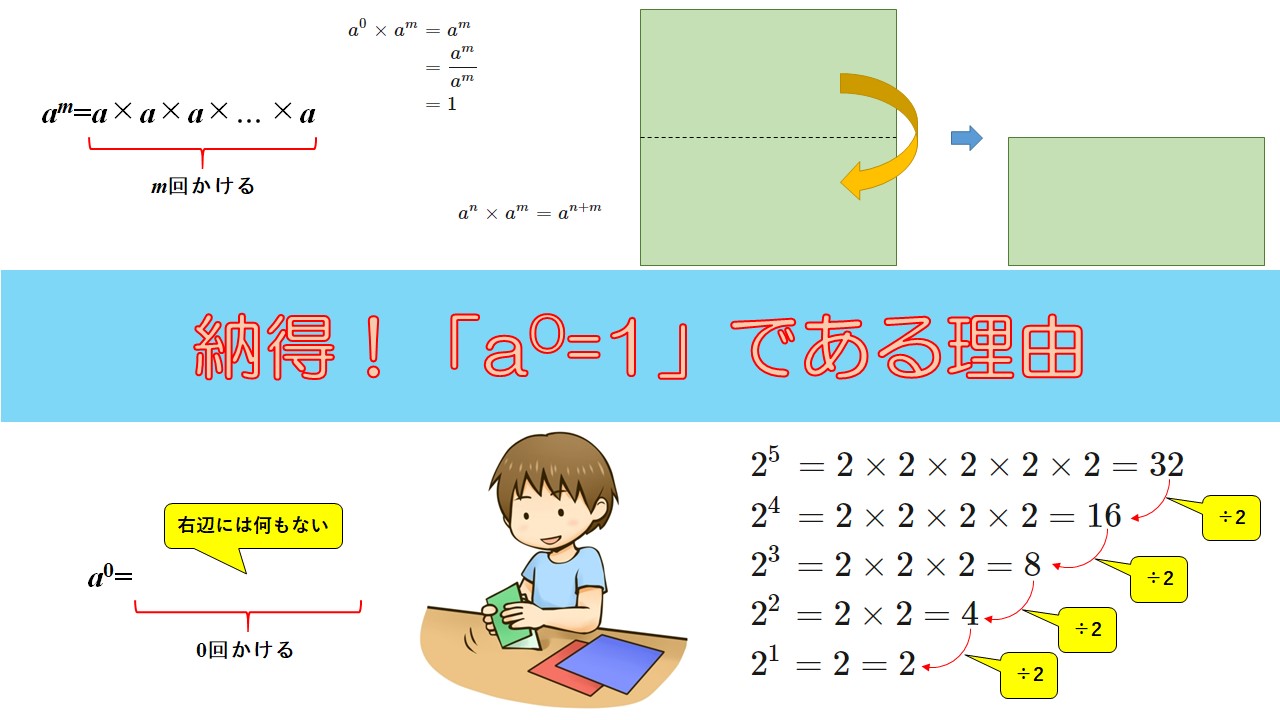
\(2\)の累乗を\(5\)から\(1\)まで徐々に減らしていった計算を考えましょう。
以下のようになります。
\begin{align}
2^5 & = 2 \times 2 \times 2 \times 2 \times 2 = 32 \\
2^4 & = 2 \times 2 \times 2 \times 2 = 16 \\
2^3 & = 2 \times 2 \times 2 = 8 \\
2^2 & = 2 \times 2 = 4 \\
2^1 & = 2 = 2
\end{align}
ここで、一番上の\(32\)を一つ下の\(16\)にするには、どんな数で割ればよいでしょうか？
当たりまえですが、\(2\)で割ればよいですね。
$$32 \div 2 = 16$$
さらに、\(16\)をその下の\(8\)にするにはまた\(2\)で割ります。
さらにさらに、\(8\)を\(4\)にするには\(2\)で割ります。
…
というように、累乗の数を減らしていくと、その一つ下の数は\(2\)で割った数になります。
このような規則性があることが分かりました。※累乗の性質を考えると当然のことではありますが…
では、\(2\)の\(0\)乗を考えてみましょう。
\begin{align}
2^5 & = 2 \times 2 \times 2 \times 2 \times 2 = 32 \\
2^4 & = 2 \times 2 \times 2 \times 2 = 16 \\
2^3 & = 2 \times 2 \times 2 = 8 \\
2^2 & = 2 \times 2 = 4 \\
2^1 & = 2 = 2 \\
2^0 & = ?
\end{align}
上の図から一つ下の値は\(2\)で割った数になるのですから、\(2^0\)の値は一つ上の\(2\)を\(2\)で割った値になるはずですね。
$$2^0 = 2 \div 2 = 1$$
すなわち\(2^0= 1\)が導けました。
これが累乗の規則性を利用した\(0\)乗が\(1\)になる説明です。
ここでは\(2\)の累乗を例に説明しましたが、もちろん、他の数字であってもまったく同じ説明で\(a^0=1\)が導けます。
階乗の定義を考え直してみる
今度は階乗の定義を考え直してみることで\(0\)の階乗を考えてみましょう。
この記事の初めにも述べたように、
\(a\)の\(m\)乗とは、\(a\)を\(m\)回掛けたもの
と定義すると考えてきました。
しかし、この定義だと\(2^0\)のときに、
「\(2\)を\(0\)回掛ける？……どゆこと？？右辺に何もないじゃん！」
となります。
そこで、この定義を次のように変更してみましょう。
\(a\)の\(m\)乗とは、\(1\)に\(a\)を\(m\)回掛けたもの
「\(1\)に」という部分を付け足しました。
これによって、例えば\(2^3\)であれば、
$$2^3 = 1 \times 2 \times 2 \times 2$$
となります。
右辺の初めの\(1\)に注目です。
もちろん、\(1\)を掛けているだけなので、計算結果は変わりません。
では、\(2\)の\(0\)乗を考えましょう。
新しい定義にしたがえば、「\(2\)の\(0\)とは、\(1\)に\(2\)を\(0\)回掛けたもの」です。
よって、
$$2^0 = 1$$
となります。
右辺にはもともと\(1\)があるため、前の定義のように「右辺には何もない」ということにならないですね。
これが、階乗の新しい定義を考えることで\(a^0=1\)を理解する方法です。
スポンサーリンク
折り紙から\(0\)乗を知る
今度は、視覚的に\(0\)乗が\(1\)であることを確認してみましょう。
ここに、一枚の折り紙があるとします。
この折り紙を下の図のように半分に折ります。
もう一度、半分にしましょう。
これで折り紙を2回折りました。
では、この折り紙を広げると、下の図のように折り目がついているはずですね。
折り目によって、分割された領域の数を数えると4つです。
すなわち、2回折ると領域が4つになったということです。
これを数式で表すと、
$$2^2 = 4$$
となります。
このように折った回数と存在する領域の数は、次の式で表現できます。
$$2^{\text{折った回数}} = \text{領域の数}$$
この式は、何回折っても成立します。
気になる人は実際に紙を折ってみて確かめみてくださいね。
では、本題です。
折った回数が\(0\)回のとき、すなわち何も折らない状態での領域はいくつでしょうか？
何も折らない状態（最初の状態）では領域は一つですよね。
ということは、上の式で表現すると以下のようになります。
\begin{align}
2^{\text{折った回数}} & = \text{領域の数} \\
2^0 & = 1
\end{align}
これで\(0\)乗が\(1\)であることがわかりました。
視覚的に\(2^0=1\)であることを理解するための方法でした。
指数法則が成り立って欲しいから\(0\)乗は\(1\)にする
最後は、指数法則を使った方法です。
指数法則を覚えていますか？下のような公式ですね。中学校の数学で習います。
$$a^n \times a^m = a^{n+m}$$
具体的に数字を入れてみましょう。
\(a=3\)、\(n=4\)、\(m=5\)とします。すると、
$$3^4 \times 3^5 = 3^{4+5} = 3^{9}$$
です。
この式が成り立っているかどうかは、左辺のそれぞれの数を、
\begin{align}
3^4 & = 3 \times 3 \times 3 \times 3 \\
3^5 & = 3 \times 3 \times 3 \times 3 \times 3
\end{align}
として、上式に代入すると、
$$3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 = 3^9$$
となり、指数法則の公式が成り立っていることがわかります。
さて、では指数法則
$$a^n \times a^m = a^{n+m}$$
において、\(n=0\)のときを考えてみましょう。
以下のように書き換えれます。
$$a^0 \times a^m = a^m$$
この式の両辺を\(a^m\)で割り、ちょちょっと計算すると、
\begin{align}
a^0 \times a^m & = a^m \\
& = \frac{a^m}{a^m} \\
& = 1
\end{align}
よって、\(a^0=1\)が現れました。
指数法則を考える上でも\(0\)乗は\(1\)としていた方が都合がよいのですね。
ここまで紹介してきたように「\(0\)乗は\(1\)」と定義しておくことで、数学的に理解しやすく、扱いやすくなります。
注意して欲しいのは、あくまで\(a^0=1\)というのは定義であって、こうなるという証明などはできません。
「\(a^0=1\)としておけば、色々と都合が良さそうだ！」ということです。
スポンサーリンク
まとめ
- \(0\)乗が\(1\)と定義される理由をいくつか紹介しました。
- まずは、規則性を使った方法です。累乗の数を減らしていったとき、その計算結果は決まった数で割っていった数と一致します。これを使って\(0\)乗が\(1\)であることを知りました。
- 二つ目は「階乗の定義」自体を考え直しました。階乗の定義に「\(1 \times\)」が掛かっていると考えることで、自然に\(a^0=1\)が納得できます。
- 三つめは視覚的に理解する方法です。紙を折った回数とそのときにできる領域の数は\(2^\text{折った回数}=\text{領域の数}\)の関係があります。0回折った時の領域の数は\(1\)であるので\(2^0=1\)が成り立ちます。
- 最後は、指数法則を使った方法でした。指数法則の公式を成り立たせるには、\(0\)乗が\(1\)になった方が都合がよいのです。