三平方の定理をパズルで証明 – 色んなパズルに挑戦してみよう
中学生の後半で習う三平方の定理ですが、なぜこのような定理が成り立つか不思議に感じたことはありませんか？
三平方の定理が成り立つことを証明するために、パズルを利用した面白い方法があります。この方法であれば、数式を視覚的に理解でき、定理が成り立つ理由をよりイメージしやすくなります。
ここでは、パズルを使った証明の方法を紹介しましょう。
三平方の定理をパズルで証明してみよう
まず、三平方の定理の復習と、なぜ三平方の定理がパズルで解けるのかを説明しましょう。
下の図のような、直角三角形があったとします。
各辺の長さは短い方からa, b, cとします。必ず、一番長い辺は直角な角度に対面しているcとなります。
三平方の定理とは、このような直角三角形の各辺に対して、次の式が成り立ちます。
$$a^2 + b^2 = c^2$$
一番長い辺（c）の二乗は、他の二つの辺（aとb）の二乗の和と等しくなるという式です。
これを図形のパズルを使って証明してみましょう。
二乗は正方形の面積を表す
まずは、”辺の二乗”とはどういうことかを考えてみましょう。
”二乗”というのは、正方形の面積のことなのです。例えば、四角形の面積の公式を思い出してください。
$$\text{四角形の面積} = \text{横の長さ} \times \text{縦の長さ}$$
ですので、横の長さと縦の長さが等しいときが正方形ですので、一辺の長さを\(a\)とすると、
$$\text{正方形の面積} = a \times a = a^2$$
となります。このことから、二乗は正方形の面積のことだというのがわかります。
三平方の定理は正方形の面積が等しいということ
上の直角三角形の各辺に正方形を作ってみましょう。すると、
のようになります。それぞれの正方形の面積は各辺の二乗になっていますね。
三平方の定理（\(a^2 + b^2 = c^2\)）の式の意味は、
一辺がaの正方形と一辺がbの正方形の面積の和は、一辺がcの正方形の面積と等しくなる
ということです。よって、緑の正方形と黄色の正方形の面積の和が、青の正方形の面積となればよいということです。
図で描くと、下のようになります。
簡単なパズルで証明してみる
上の図で、小さい二つの正方形（緑と黄色）をバラバラにして青い正方形にピッタリ詰め込めれば、三平方の定理、
$$a^2 + b^2 = c^2$$
が成り立つことを証明できたことになります。やってみましょう。
まず、緑と黄色の正方形を以下の図のように分割します。点線が切り口です。
バラバラにしたパーツを青い正方形にうまく当てはめると、
とこんな感じに、なんとピッタリ収まります！
これで、三平方の定理がパズルみたいな方法で証明できちゃいましたね。
スポンサーリンク
作り方は無限？色々なパズルに挑戦してみよう
先ほど紹介した以外にもパズルの作り方は、「無限なの？」と思えるほどたくさんあります。
その中のいくつかを紹介していきましょう。
また、パズルにPDFを用意していますので、ダウンロードして印刷して使うこともできます↓
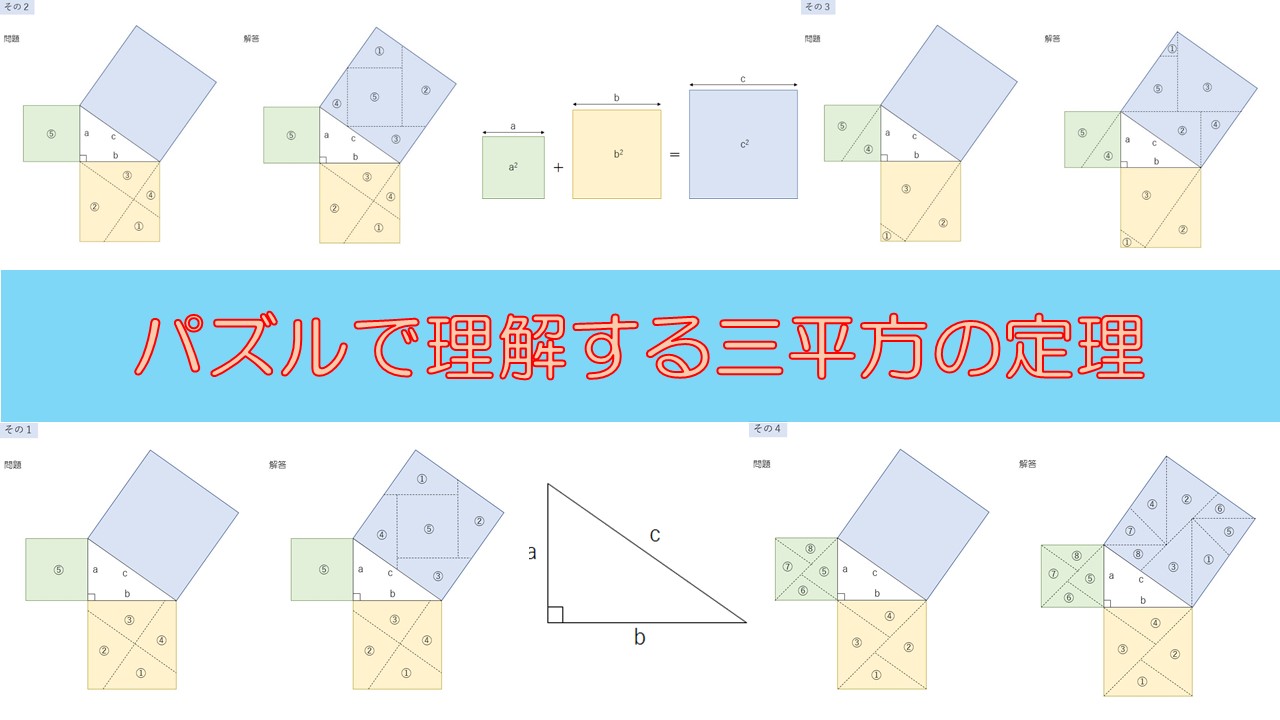
その①
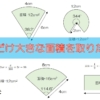
一番小さな緑の正方形はそのまま使うパターンのパズルです。解答は、黄色の正方形を分解したパーツで、緑の正方形を囲むように配置します。
その②
これも緑の正方形は分割せずにそのまま使うタイプのパズルです。ただし、黄色の正方形の切り方が少し違います。
その③
初めに例でみたパズルと一緒の切り方です。黄色の正方形を切るときの角度が異なっているだけです。
その④
今度は、正方形の分割数が八つと多めです。黄色と緑の正方形を四つずつに分割しています。解答もかなり複雑で難易度高めとなっています。
その⑤
こちらも分割数が八つのバージョンです。
これらをPDFにまとめました。印刷してご利用ください↓
まとめ
- 二乗とは、正方形の面積を表す
- 三平方の定理は、直角三角形の各辺を一辺とした正方形の面積の関係を表すものである
- 小さい二つの正方形の面積が、大きな正方形の面積に等しくなる
- パズルのように正方形を分割して当てはめていくと、三平方の定理が成り立っていることが分かる