「2進数とは」をわかりやすく解説 – 10進数がわかれば2進数もわかる!
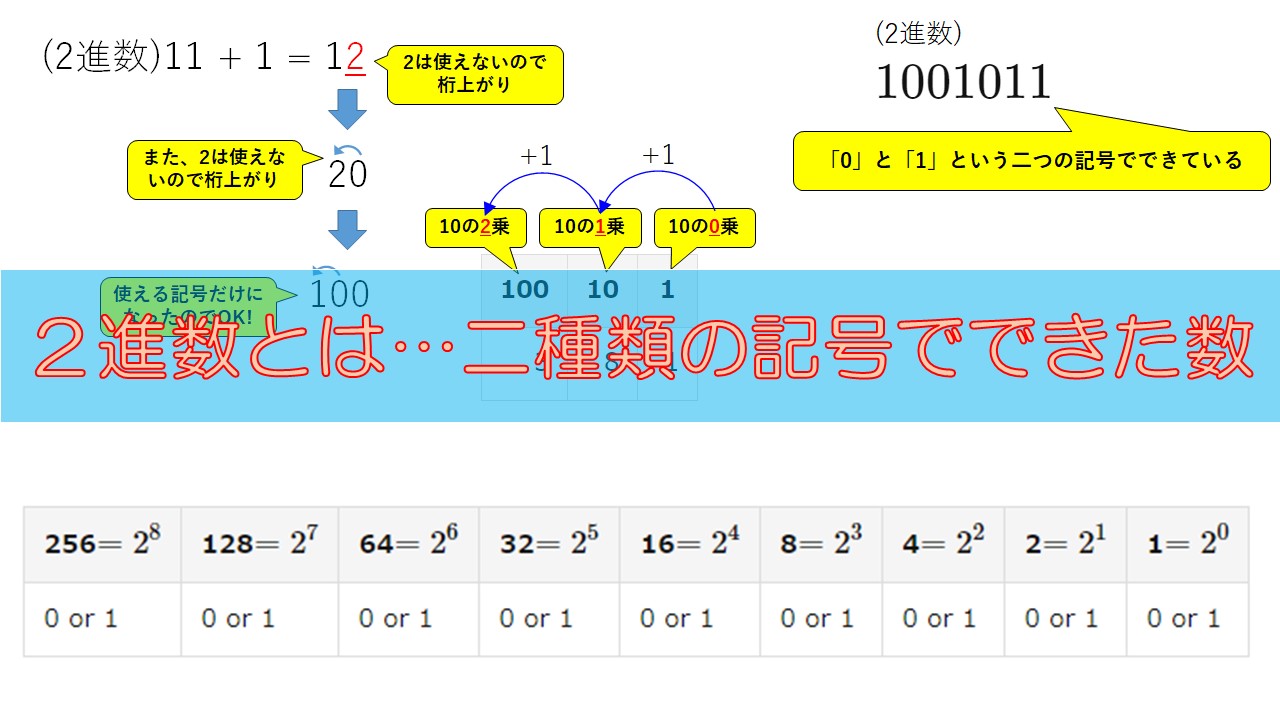
「2進数」とは何なのかをわかりやすく解説しています。
また、2進数を10進数に簡単に変換する方法、もしくはその逆の変換方法についても後半で解説しています。
この記事で2進数とは何なのかを完全に理解してしまいましょう!
2進数(にしんすう)とは
詳しい説明に入る前に、いきなり「2進数(にしんすう)」とは何なのかを一言で言ってしまうと、
2進数とは、2種類の記号で数を表す方法
です。
例えば、
- \(101\)
- \(1001011\)
- \(1111111\)
のような\(1\)と\(0\)が並んだ表現を見たことがあるのではないでしょうか?
この段階で詳しく意味がわからなくてもいいのですが、これが「2進数」で表した数の表現です。
上の重要ポイントで言った「2種類の記号」とは、ここでは\(0\)と\(1\)のことです。
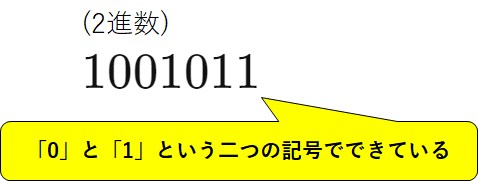
ちなみに、これらの2進数は我々が普段使っている数で表現すると、それぞれ、
- \(101 = 5\text{(10進数で表現)}\)
- \(1001011 = 75\text{(10進数で表現)}\)
- \(1111111 = 127\text{(10進数で表現)}\)
を表しています。上式の右辺が普段わたしたちが使っている方法で表現したときの数です。
この我々が普段使っている数の表現を「10進数」といいます。
スポンサーリンク
10進数とは
まずは、2進数を見ていく前に、我々が普段使っている10進数について考えていきましょう。
2進数は「2種類の記号で数を表す方法」でした。一方、10進数は「10種類の記号で数を表す方法」です。
では、10種類の記号とはなんでしょうか?それは、
$$0, 1, 2, 3, 4, 5, 6, 7, 8, 9$$
です。私たちは普段、これらを「記号だ」と考えていないですが、これらはただの記号です。
私たちは、これらの10個の記号に関しては、その記号が表す数を暗記しているのです。
例えば、
- 「”0”は何もないことを表す記号だな」
- 「”1”は何か一つだけあることを表す記号だな」
- 「”2”は”1”よりも1つ大きい数を表す記号だ」
などと覚えています。
表現したい数がどんなに大きくても、これらの10個の記号を使えば表現できてしまいますよね。もう新しい記号を増やして、それを覚える必要はありません。
なぜかというと、\(9\)よりも大きい数(10以上の数)を表現しようと思ったら、桁を上げればいいからです。
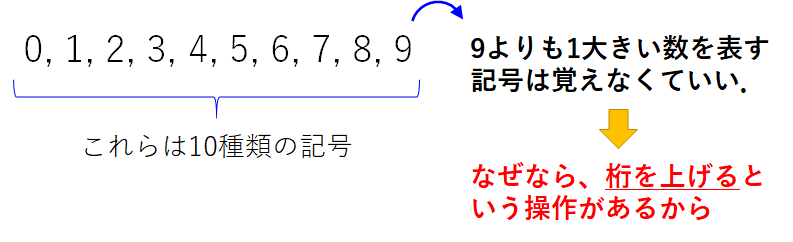
ここが非常に大事なところです。
10進数での表現は\(10\)以上なれば桁を上げることで、どんなに大きな数も表現できるようになる
この考え方は2進数を考えるときにも役に立ってきます。
「数を表現する」ということ
ここからが今回のテーマの重要なパートです。まずは、10進数の数を詳しく見ていきましょう。
10進数で表された「\(381\)」という数について考えてみます。
これは、
- \(1\)が1つ
- \(10\)が8つ
- \(100\)が3つ
あるということです。すなわち、
$$381 = (100 \times 3) + (10 \times 8) + (1 \times 3)$$
ということですね。
以下の表を見てください。
| 100 | 10 | 1 |
|---|---|---|
| 3 | 8 | 1 |
これは、\(381\)を表現するためには、100が3つ、10が8つ、1が1つ必要ということを表で表したものです。
この後に、2進数について考えていくのですが、この表での表現が便利になります。
この表の上の段に書かれてある100, 10, 1というのは、10の\(n\)乗になっていることを覚えておきましょう。
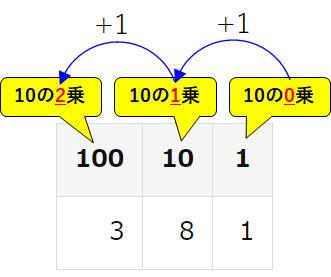
そして、\(n\)乗の\(n\)は一番桁が小さい方から0で始まり、0,1,2,3,…と桁が大きくなるにつれ、一つずつ増えていきます。
余談ですが、\(10\)の\(0\)乗はなぜ\(1\)になるのでしょうか?
\(10\)だけではなく、どんな数字も\(0\)乗すると\(1\)ですよね。\(0\)の\(0\)乗ですら\(1\)です。
なぜそうなるのか不思議に思った人に、以下の記事を書きました。よかったら読んでみてください。
スポンサーリンク
2進数
ところでなぜ、我々が普段使っている数の記号は10種類なのでしょうか。言い換えると、なぜ我々は10進数を使っているのでしょうか?
それは…私は知りません。大昔の人がそうすると決めて、それが現在まで伝わってきたのかもしれません。
何か10という数にすることで都合がよいことが多かったのかもしれません。人間の手の指は10本ですし。
ですが、数を表すのに10種類も記号はいらないのです。
数を表現するのに、必要な最低限の数は2種類です。そして、それが2進数です。
その2種類の記号は一般的には\(0\)と\(1\)が使われます。

10進数は10になると桁を繰り上げましたが、2進数は2種類しか記号を使えないのですから、2になったら桁を繰り上げないといけません。※「2」という記号は使えないからです。
つまり、0,1までは10進数と同様ですが、2という記号はないため、桁を繰り上げて、(2進数)10と表現します。
| 10進数 | 2進数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
※ここからは、2進数表現と10進数表現が混在するため、どちらの表現かを数字の前の(X進数)で示すことにします。
例えば、
(10進数)10
と書いた場合、10進数表現での10を表します。我々が普段使っている表現ですね。
一方、
(2進数)10
と書いた場合、2進数表現での10を表します。これは10進数表現での2となります。
(2進数)10に、+1して(10進数)3を表現するには(2進数)11となります。
さらに、+1して(10進数)4は(2進数)11に+1をするので桁上がりをしますが、0と1という記号しか使えない制限のため、以下のように桁上がりを繰り返します。
まず、(2進数)11に+1をして、
$$11 + 1 = 12$$
としたいところですが、一番右の「2」は使えません。なので、桁上がりして一つ左の1に+1をして、右の数値は0とします↓
$$12 \rightarrow 20$$
しかし、左にも「2」が出てきてしまいますので、さらに左に桁上がりして、
$$20 \rightarrow 100$$
となります。
ここまでの変化をわかりやすく下の図でイメージしました。
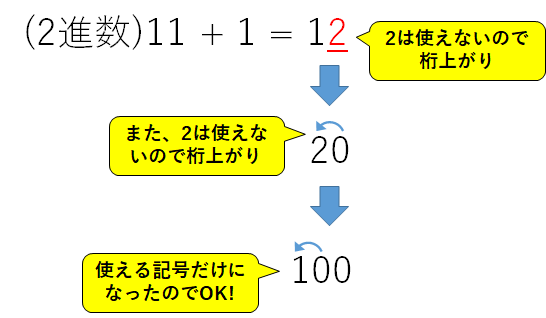
よって、(10進数)4は(2進数)100となります。
$$(\text{10進数})4 = (\text{2進数})100$$
お気づきの通り、2進数はすぐに桁が上がるため、少しでも数を増やすのが大変です。
このように、進めていき(10進数)10までに対応する2進数の表現を以下の表にまとめました。
| 10進数 | 2進数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
このように、2進数は桁上がりを繰り返していき、どんなに大きな数でも表現することができます。
10進数を2進数の表現に変換する簡単な方法
2進数は、上で説明したように、桁上がりを考えていけば、それに対応している10進数の数がわかります。
しかし、一つ一つ順番に考えていては、2進数から10進数への変換もしくはその逆の変換(10進数から2進数へ)は、とてつもない時間がかかってしまいます。
そこで、ある10進数の数を簡単に2進数に変換する方法があります。
それが、表を使った方法です。10進数の数を表で説明したことを思い出しましょう。
例えば、(10進数)381は、100が3つ、10が8つ、1が1つで構成されているので、
| 100 | 10 | 1 |
|---|---|---|
| 3 | 8 | 1 |
という表で表現できることを紹介しました。
この表の上の行(100,10,1)は10の\(n\)乗で、右から左に増えていってましたね。

同じように、2進数も表で表現してみます。
ただし、2進数の場合は2の\(n\)乗が上の行に入ります。この表の上の数は10進数表示です。
| 256\(=2^8\) | 128\(=2^7\) | 64\(=2^6\) | 32\(=2^5\) | 16\(=2^4\) | 8\(=2^3\) | 4\(=2^2\) | 2\(=2^1\) | 1\(=2^0\) |
|---|---|---|---|---|---|---|---|---|
| 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 |
表現する数は上の例と同じ(10進数)381としましょう。その場合、表の上の数を見て、(10進数)381になるように「1」を入れていきます。
すると、以下のような表が出来上がります。
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
つまり、1が入っている場所の数字を足すと(10進数)381となっているのです。確かめてみましょう。
1が入っている場所の数字は、左から\(1, 4, 8, 16, 32, 64, 256\)ですね。これを全部足しましょう。
$$1+4+8+16+32+64+256=381$$
ちゃんと381となっていますね。
このような表が書けたら、あとは表の0と1を並べて、
101111101
とすれば、これが(10進数)381を2進数で表現した形となります。簡単ですね。
逆に、2進数から10進数への変換も同じようにするだけです。
(2進数)101111101があり、これを10進数で表現した数を知りたい場合は、同じように表を作り、
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
2進数で1が入っている列の数字(赤字)を足すだけです。
$$256 + 64 + 32 + 16 + 8 + 4 + 1 = 381$$
色んな変換をみてみよう
では、いくつか変換してみましょう。そんなにめんどくさい計算の例は出しませんので、まずは自分で解いてみてください。
10進数から2進数へ
10進数の28を2進数で表現せよ。
では解いてみましょう。
まずは、表を書くのでしたね。10進数で28ですので、以下の表のように16までの表を準備しておけばよいでしょう。
| 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|
| 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 | 0 or 1 |
この表の下の行に、28にするために使う数字(足す数字)の場所に1を入れていくのでした。
※16までの表でよい理由は、16の次は32ですが、これは28より大きいからです。仮に32の場所に1を入れて32を使うことにしてしまうと、それだけで28を超えてしまいます。よって表には32以上は必要ないのです。
では、使う数字に1を入れていきましょう。使わない数字には0を入れます。すると、
| 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 |
となります。
$$16 + 8 + 4 = 28$$
ですね。よって(10進数)28は2進数で表現すると、
11100
となります。
2進数から10進数へ
では、次は2進数から10進数にする例題にもトライしておきましょう。
2進数の10101を10進数で表現せよ。
では解いてみましょう。
まずは、同じように表を書きますね。ただし、今回は2進数がわかっているので、表ははじめからすべて埋まっています↓
| 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 |
続いて、1がある場所の10進数の数字を全部足して、
$$16+4+1=21$$
です。よって、(2進数)10101を10進数で表現すると21ということになります。
どうでしょうか?これで変換も完璧ですね!
2進数で表現できない数はない?
ここで、こんな疑問が浮かんだ方もいるかもしれません。
「2進数で表現できない10進数もあるのでは?」
例えば、十進数の\(30001\)という数字は2進数では表現できないのでは?という感じですね。
しかし、そんな数はありません。どんな数(厳密には整数)も必ず2進数で表現することができます。
いろんな10進数の数に対して、表を使って2進数に変換できるか試してみましょう。表現できない数が見つかれば、それは人類初の大発見です。
スポンサーリンク
2進数のメリットとデメリット
メリット
2進数を使うメリットとは何でしょうか?
2進数が特に活躍している分野はコンピュータの分野です。
コンピュータは難しい計算を一瞬で計算しているように見えますが、実は2の記号しか使えないんです。
ON(オン)かOFF(オフ)だけしか表現できないんです。
もっと正確に表現すると、電圧が0Vか、そうでないかだけを使って計算しています。コンピュータの指は二本なんですね。
そして、もう一つのメリットは記号を2種類しか覚えなくていいことでしょうか。
1と0を覚えて終わりです。後は計算方法を理解すれば、すべての数を表現できるようになるからです。
例えば、世界が100進数を使っていたらどうでしょうか?100種類の記号をまずは覚えないといけませんね。我々の世界が10進数でよかった…。
デメリット
これはお察しのとおり、凄く表現が長くなることです。
上の例で紹介した10進数で”381”という数字も、2進数で表現すると”101111101”と9桁にもなりました。
これでは、小さな数を書くのも大変ですし、「あれ?1が一個少ないぞ?」とか間違いが多くなりそうですね。
まとめ
- 2進数とは、「二種類の記号で数を表現したもの」です。
- その二種類の記号とは”1”と”0”であり、10進数の381を表現すると”101111101”などとなります。
- 2進数から10進数への変換、もしくはその逆の変換は表を使いましょう。
- 2進数で表現できない数(整数)はありません。


























ディスカッション
コメント一覧
すると、以下のような表が出来上がります。
256 128 64 32 16 8 4 2 1
1 0 1 1 1 1 1 0 1
つまり、1が入っている場所の数字を足すと(10進数)381となっているのです。確かめてみましょう。
ここの部分が理解できず苦しんでいます。
解説お願いできますでしょうか?
少し細かく説明すると381を超えない一番大きい乗数を出します。この場合だと256ですね。
そして256から1までを足したら絶対に381になります。256から381までは125空いています。
その必要な数の125は128から1までのどれかを1つ足せば絶対に125になります。そしてそのたせる数の下に1と書きましょう。この場合だと、64+32+16+8+4+1です。なので表に表すと、
256 128 64 32 16 8 4 2 1
0 1 1 1 1 1 1 0 1となります。
だから、381の二進数は101111101となります。
できるだけ細かく教えましたが、わからなかったらすいません。
少し細かく説明すると381を超えない一番大きい乗数を出します。この場合だと256ですね。
そして256から1までを足したら絶対に381になります。256から381までは125空いています。
その必要な数の125は128から1までのどれかを1つ足せば絶対に125なります。そしてその足せる数の下に1と書きましょう。この場合だと、64+32+16+8+4+1です。なので表に表すと、
256 128 64 32 16 8 4 2 1
1 0 1 1 1 1 1 0 1となります。
だから、381の二進数は101111101になります。
できるだけ細かく教えましたが、わからなかったらすいません。
とても分かりやすかったです!(学校の先生よりも分かりやすかったw)ありがとうございました
Javaの学習でつまづいていた部分だったので、とても理解しやすく助かりました!