【中学1年数学（比例と反比例）】「関数とは」をわかりやすく解説 – 「関数であるもの」を選ぶ問題を解けるようになろう
- 「関数」とは？をわかりやすく説明してほしい人
- 「関数であるもの」を選ぶ問題を解くのが苦手な人
中学1年生の数学で勉強する比例・反比例の単元で、「関数（かんすう）」というワードが登場します。
このページでは、まず「関数」とは何なのかを丁寧に解説していきます。関数を理解することが、そのあとに習う比例や反比例を理解することの第一歩です。
つぎに、「関数であるものはどれか？」というフレーズが登場する問題を解けるようになるための解説を行っていきます。
関数という単語は、中学数学の様々なところで登場しますので、これを正確にわかっておくことはとても重要です。
できるだけわかりやすい親切な説明を心掛けますので、ここで関数とはどのようなものなのかを理解してしまいましょう！
「関数（かんすう）」とは
まずは、「関数」とは何なのかを説明します。
そのために、一つ問題を解いてみましょう。下の文章問題を解いてみてください。簡単です。
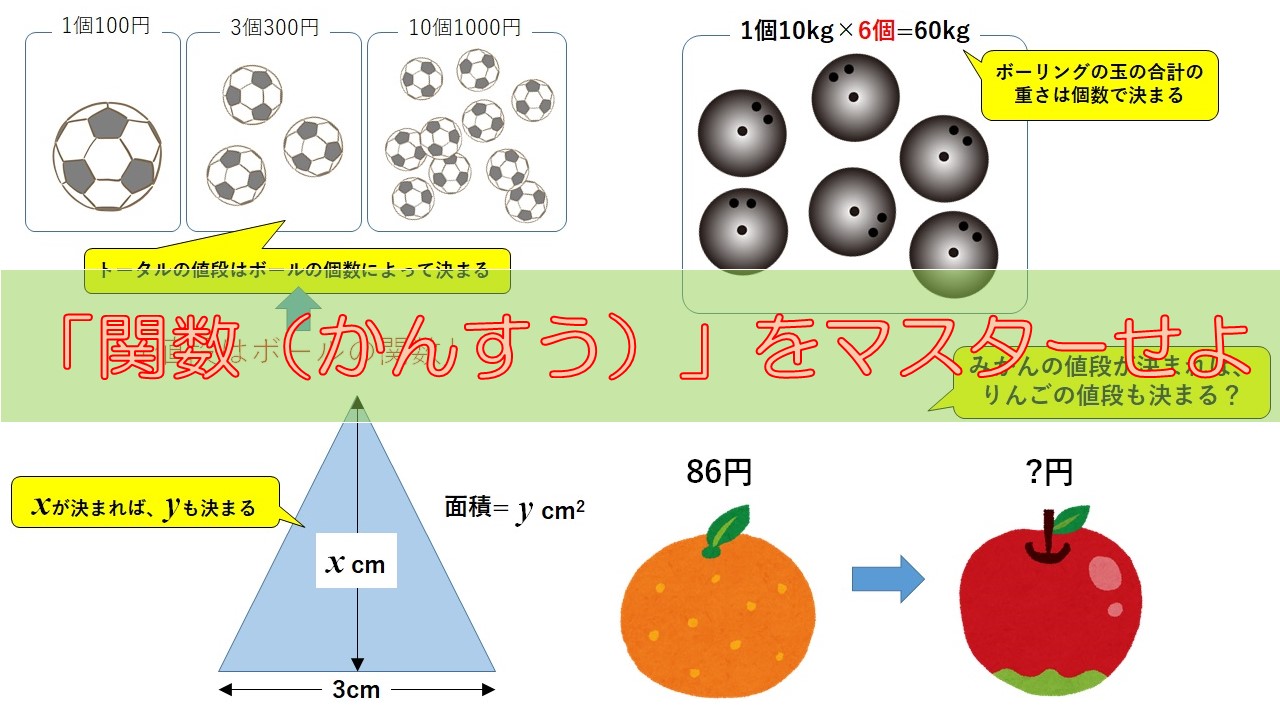
一個\(100\)円のボールがあります。このボールを5個買ったら値段はいくらになるでしょうか？
この問題を式で表すと、
$$100 \times 5 = 500$$
ですね。
よって、答えは\(500\)円です。簡単に解けたと思います。
このとき、値段は何によって決まるでしょうか？
ボールの一個の値段は\(100\)円と決まっているのですから、この場合は、ボールの個数によって決まります。
ボールを2個買えば値段は\(200\)円ですし、ボールを10個買えば\(1000\)円です。
このようにボールの個数が決まれば、値段が決まります。
このようなとき、「値段はボールの関数である」といいます。
これをもっと一般的（ボールに対してだけではなく、どんなことにも言えるように）に言うと、
「ある値（\(x\)）が決まれば、もう一方の値（\(y\)）も1つに決まる」とき、\(y\)は\(x\)の関数である
となります。
先ほどの文章問題の例で言うと、
- \(x\) → ボールの個数
- \(y\) → 値段
ということになります。
\(x\)が決まれば、\(y\)も決まってしまいますよね。よって、\(y\)は\(x\)の関数です。
つまり、値段はボールの関数ということが言えます。
スポンサーリンク
その他の関数の例
上では、ボールを例に説明しましたが、他にもいろいろな関数の例を考えてみましょう。
ボールの重さと個数
次の文章をみてください。
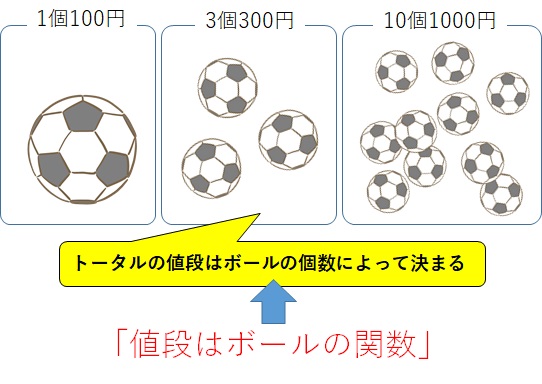
1個10kgのボーリング玉をいくつか集めた合計の重さは、集めたボーリング玉の個数の関数である
これは正しいでしょうか？
\(x\)が決まると\(y\)が決まるものを、「\(y\)は\(x\)の関数」と言いました。
ここで、
- \(x\) → ボーリング玉の個数
- \(y\) → （ボーリング玉の）合計の重さ
とすると、「ボーリング玉の個数」が決まれば、「合計の重さ」も決まります。
よって、これらは関数であり、上の文は正しいということになります。
三角形の面積と高さ
次は少し違う例を出します。
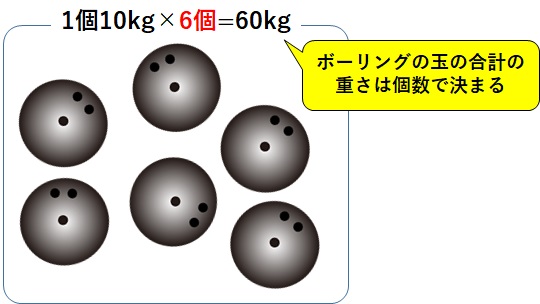
底辺が3cmの三角形の面積は、（三角形の）高さの関数である
これは正しいでしょうか？
面積を\(y\)とし高さを\(x\)とすると、\(x\)が決まれば\(y\)が決まりますね。
- \(x\) → 三角形の高さ
- \(y\) → 三角形の面積
ですので、「底辺が3cmの三角形の面積は、高さの関数」は正しいです。
長方形の縦と横の辺の長さ
最後にもう一つ、
面積が\(10\)cm2の長方形の縦の長さは、横の長さの関数である
これはどうでしょうか？
これも、
- \(x\) → 長方形の横の長さ
- \(y\) → 長方形の縦の長さ
とすれば、\(x\)が決まると、面積を10cm2にするために自動的に\(y\)も決まってしまいます。
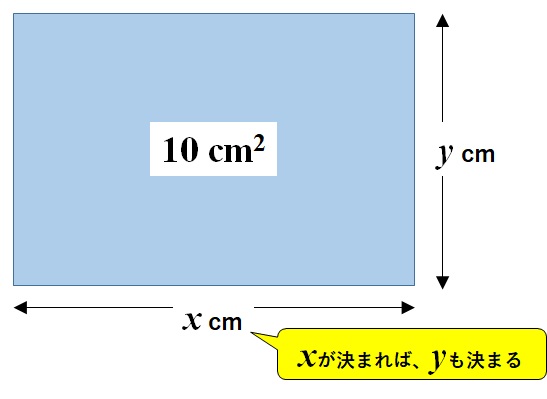
よって、\(y\)は\(x\)の関数であり、上の文は正しいです。
関数ではない例
りんごの値段とみかんの値段
「どのようなものが関数であるか」わかってきましたか？
では、以下の文はどうでしょうか？
りんご1個の値段は、みかん1個の値段の関数である
これは、関数ではありませんよね。
みかんの値段が決まったからといって、りんごの値段は決まりません。りんごはりんごで、みかんの値段に関係なく値段を決めることができます。
自然数と約数
もう一つ問題です。以下の文はどうでしょうか？
ある自然数を\(x\)とするとき、その約数\(y\)は\(x\)の関数である
これはどうでしょうか？「自然数」と「約数」を忘れている人は下の説明から思い出しましょう。
自然数とは、1以上の整数のことです。つまり、
$$\text{自然数} = 1, \quad 2, \quad 3, \quad 4, \quad \cdots$$
のことです。
（余談）\(0\)も自然数に含める人もいるらしい…
約数とは、ある整数を割り切れる数です。
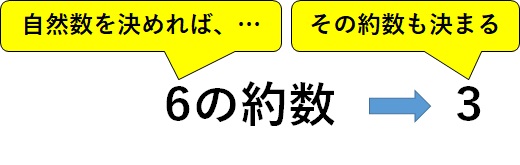
例えば、ある整数を\(6\)とすると、\(6\)の約数はこれを割り切れる数なので、
$$6\text{の約数} = 1, \quad 2, \quad 3, \quad 6$$
となります。思い出しましたか？
では、「関数」の話に戻りましょう。
「ある自然数を\(x\)とするとき、その約数\(y\)は\(x\)の関数である」
は正しいのかという問題でした。
一見、正しいようにも思えます。
例えば、ある自然数を\(6\)とすると、その約数は例えば\(3\)ですから、\(x\)（自然数）を決めれば\(y\)（約数）は決まります。
$$x = 6 \rightarrow y = 3$$
しかし、「これは関数！」ではないんです。もう一度、「関数とは」を確認してみましょう。
「ある値（\(x\)）が決まれば、もう一方の値（\(y\)）も1つに決まる」とき、\(y\)は\(x\)の関数である
この「1つに」という部分が重要です。
自然数\(6\)の約数は\(3\)だけではなく、\(1\)や\(2\)や\(6\)も\(6\)の約数ですよね。
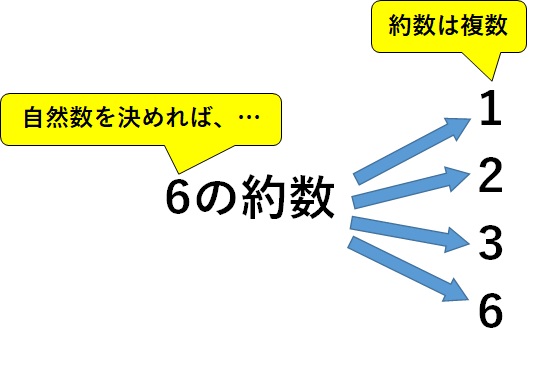
なので、\(x\)（自然数）が決まっても\(y\)（約数）は1つには決まらない。よって、\(y\)は\(x\)の関数ではないのです。
ここまでで、関数の説明は終わりです。もう一度、大事な部分を復習しましょう。
関数とは、
- 一方(\(x\))が決まると、もう一方(\(y\))が決まるととき、\(y\)は\(x\)の関数
- ただし、一つの\(x\)に対して、複数の\(y\)が存在するとは関数ではない
これを覚えておきましょう。
スポンサーリンク
「関数であるもの」を選ぶ問題
関数とは何かがわかったところで、「関数であるもの」というフレーズが登場する数学の問題を解いてみましょう。
ここまでがきちんと理解できていれば、絶対に解けるはずです。
では、問題です。
次のうち、\(y\)が\(x\)の関数であるものをすべて選びなさい。
- 1本\(20\)円の鉛筆を\(x\)本買い、\(500\)円出したときのおつり\(y\)円
- 曲のタイトルの文字数\(x\)と曲の長さ\(y\)
- 1個\(33\)kgの段ボールが\(x\)個の重さ\(y\)
- 自然数\(x\)の倍数\(y\)
先に答えを言うと、関数であるものは、
１と３
です。
このような問題を解くときは次のことを考えながら、解くことがコツです。
- 「\(x\)が決まったら\(y\)は決まるだろうか？」
- 「そして、それは1つだけだろうか？」
では、「１．1本\(20\)円の鉛筆を\(x\)本買い、\(500\)円出したときのおつり\(y\)円」から考えていきましょう。
自分が鉛筆の購入者であると思ってください。
\(x\)は鉛筆の本数であり、1本20円なのは決まっているのですから、買う本数さえ決まれば、払う代金が決まります。
そして、こちらは\(500\)円出すことが決まっているので（自分はいま\(500\)円玉しか持ってなかったのかも）、買う本数\(x\)が決まればおつりも決まりそうです。
よって、この問題文の\(y\)は\(x\)の関数です。
次は、「２．曲のタイトルの文字数\(x\)と曲の長さ\(y\)」を考えてみましょう。
曲のタイトルの文字数（タイトルの長さ）が決まれば、その曲の長さは決まるでしょうか？
決まらないですよね。曲の長さとその曲のタイトルの長さは関係ありません。ですので、この文章の\(y\)は\(x\)の関数ではありません。
日本でもっとも長い曲のタイトルは、
「それでも暮らしは続くから 全てを 今 忘れてしまう為には 全てを 今 知っている事が条件で 僕にはとても無理だから 一つずつ忘れて行く為に 愛する人達と手を取り 分け合って せめて思い出さないように 暮らしを続けて行くのです」
だそうです（2020年2月時点※メジャーのみ。
では、「３．1個\(33\)kgの段ボールが\(x\)個の重さ\(y\)」はどうでしょうか？
これは、イメージしやすいですね。一つ33kgの段ボールを持つことを想像してください。その重さ（\(y\)）は持つ個数（\(x\)）だけで決まります。
よって、この文の\(y\)は\(x\)の関数です。
最後に、「４．自然数\(x\)の倍数\(y\)」です。
これは、自然数\(x\)が決まれば、その倍数\(y\)は決まります。
例えば、\(x\)が\(3\)であれば、例えばその倍数である\(y\)は\(6\)です。
\(x\)が決まれば\(y\)も決まりそうですが、ここで注意すべきは「\(y\)が一つに決まるかどうか」です。
\(x\)が\(3\)の場合は、その倍数は\(6\)以外にも\(9\)や\(12\)などたくさんありますね。これでは、一つに決まりません。
ですので、これは関数とは呼べません。「この文の\(y\)は\(x\)の関数ではない」となります。
まとめ
ではまとめです。
まず、関数とは、
「ある値（\(x\)）が決まれば、もう一方の値（\(y\)）も1つに決まる」とき、\(y\)は\(x\)の関数である
でした。
注意すべきは、「1つに」というフレーズでしたね。
「関数であるもの」を選ぶ問題を解くときに考えることは、
- 「\(x\)が決まったら\(y\)は決まるだろうか？」
- 「そして、それ\(y\)は1つだけだろうか？」
でした。
これを意識して解けば、どんな問題でも解けるはずですよ。