【中学2年数学（連立方程式）】加減法を使った連立方程式の解き方 – 実際に問題を解きながら解説

2020年4月4日

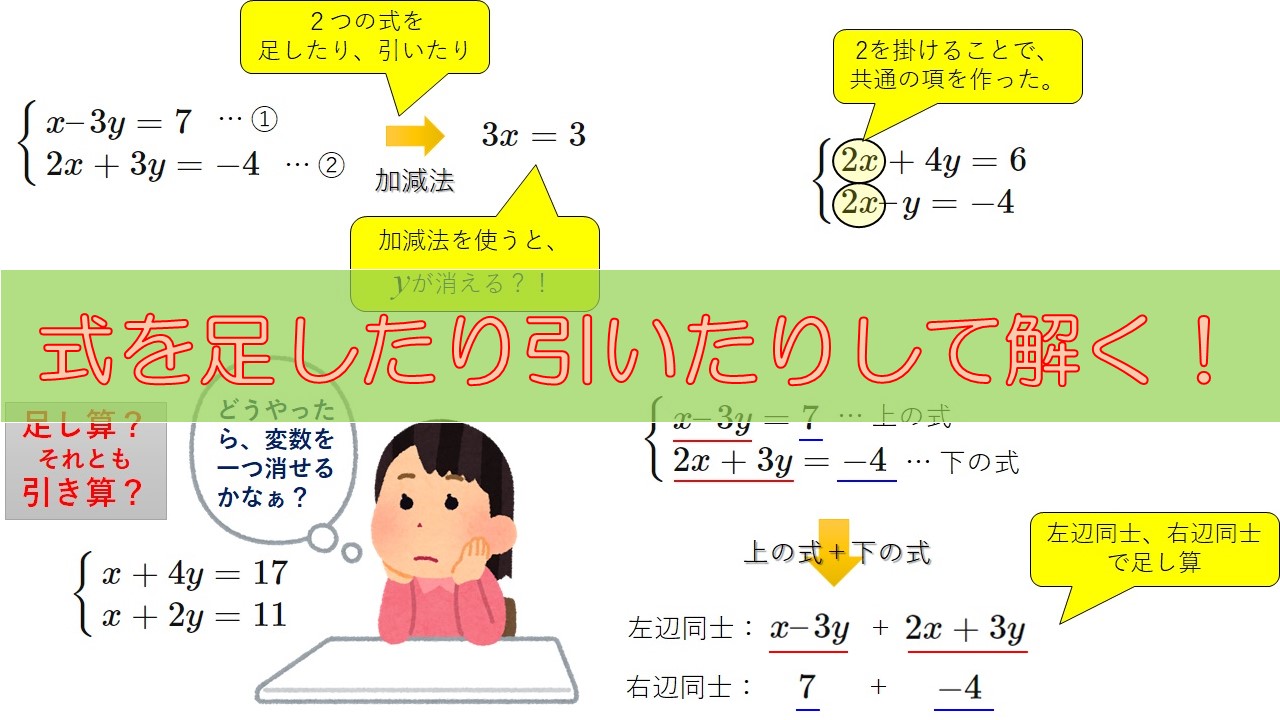
加減法を使った連立方程式の解き方

加減法（かげんほう）を使って連立方程式を解くとは、一言でいうと、次のような作業をすることです。

 

具体的に以下のような連立方程式を考えましょう↓

\begin{eqnarray}
\begin{cases}
x – 3y = 7 & \\
2x + 3y = -4 &
\end{cases}
\end{eqnarray}

連立方程式を解くとは、問題の式の\(x\)と\(y\)の値を決めてやることでしたね。

ですが、上の問題の式を見ても、\(x\)と\(y\)の値が何になるのかは、すぐにはわかりません。

初めて連立方程式を解く人にとっては、ここからどうすればいいのかもわかりません。混乱してしまいます。

 

なぜ、そのような混乱が起こるかというと、変数が2つもあるからです。

上の式のままだと、\(x\)と\(y\)の2つの変数が何になるかを、同時に考えないといけないから難しく感じてしまいます。

 

そこで、二つの変数を一つにすることを考えます。

そのためには、\(x\)か\(y\)の変数をどちらか一つ消さなければいけません。

変数を消すための方法の一つが加減法（かげんほう）と呼ばれる方法です。

 

加減法は、その名の通り、二つの式を足したり（加算）、引いたり（減算）して\(x\)もしくは\(y\)を消すように式を操作していきます。

 

スポンサーリンク

どちらかの文字を消す

では、実際に先ほどの連立方程式を加減法で解いていきましょう。もう一度問題を書いておきます↓

まず、上の式と下の式を足してみましょう。

式同士の足し算をするときは、左辺同士、右辺同士でそれぞれ計算します。※これは引き算する場合も同じです。

 

まずは、左辺同士を足すと、

\begin{align}
(x – 3y) + (2x + 3y) &= x – 3y + 2x + 3y\\
&= 3x
\end{align}

となります。※【ワンポイントアドバイス】式同士の計算には必ずそれぞれに括弧を付けてから計算しましょう。ミスが減りますよ。

なんと、\(y\)が消えて、\(x\)だけの式となりました。

$$\text{左辺同士の足し算} = 3x$$

 

次に、右辺同士の足し算です。といっても右辺はどちらも数字だけですので、

$$7 + (-4) = 7 – 4 = 3$$

となります。

よって、

$$\text{右辺同士の足し算} = 3$$

です。

 

最後に、右辺と左辺は＝（イコール）で結べますので、

\begin{align}
\text{左辺同士の足し算} &= \text{右辺同士の足し算}\\
3x &= 3
\end{align}

となります。これは、簡単に解けて、\(x=1\)ですね。

このように、連立方程式の2式を足したり引いたりして、変数を1つだけにします（この場合は\(x\)だけにした）。

すると、解ける式の形になるのです。

 

あとは、\(x=1\)を元の連立方程式のどちらかの式に代入すれば、\(y\)も求まります。

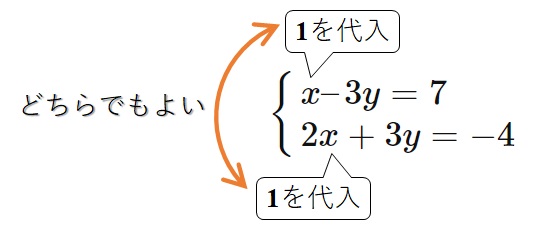
どちらの式を使っても同じ答えになるのですが、計算が楽そうな式に代入するとよいでしょう。

ここでは、上の式（\(x – 3y = 7\)）が楽そうなので、そちらに代入します↓

\begin{align}
x – 3y &= 7\\
1 – 3y &= 7\\
– 3y &= 6\\
y &= 6 \div (-3)\\
y &= -2
\end{align}

これで\(y\)もわかったので、連立方程式が解けました。答えは、

\begin{eqnarray}
\begin{cases}
x = 1 & \\
y = -2 &
\end{cases}
\end{eqnarray}

です。

 

\(y\)を消す場合

先ほどは、2つの式同士を足して、初めに\(y\)を消しました。

ですが、必ず\(y\)を消す必要はなく、別に\(x\)を消してもいいんです。

 

\(x\)を最初に消す例として、以下の問題を考えましょう。

では、この2つの式を足しましょう。

まずは、左辺同士から足し算をして、

\begin{align}
(-x + 4y) + (x + 2y) &= -x + 4y + x + 2y\\
&= 4y + 2y\\
&= 6y
\end{align}

よって、

$$\text{左辺同士の足し算} = 6y$$

です。

今度は\(x\)が消えて、\(y\)だけの式になりましたね。

 

次に右辺同士の足し算をして、

$$1 + 11 = 12$$

ですね。よって、

$$\text{右辺同士の足し算} = 12$$

です。

 

最後に、両辺をイコール(=)で結んで、

\begin{align}
\text{左辺同士の足し算} &= \text{右辺同士の足し算}\\
6y = 12\\
y = 2
\end{align}

とします。これで、\(y\)が求まりました。

 

そして、\(y=2\)を2式のどちらかの式に代入します。

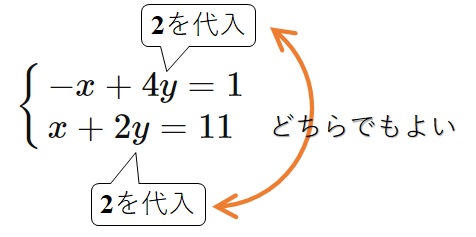
ここでは、下の式に代入することにします。

\begin{align}
x + 2y &= 1\\
x + 2 \times 2 &= 1\\
x + 4 &= 1\\
x &= – 3
\end{align}

これで、\(x\)も求まりました。

 

よって、連立方程式の答えは、

\begin{eqnarray}
\begin{cases}
x = -3 & \\
y = 2 &
\end{cases}
\end{eqnarray}

となります。

以上、\(x\)を消す場合の例でした。

 

\(x\)と\(y\)のどちらを消せばいいの？

ここまでの説明を聞いて、

「えっ？結局、\(x\)と\(y\)のどちらを消せばいいの？」

と思った人もいるかもしれません。

それに対する答えは、

「どっちでもいいよ。」

です。

 

どちらを消しても、最終的な答えは変わりません。

しかし、どちらを消すかで、”消しやすさ”は変わってきます。

ですので、式を見て、

「消しやすそうな方を消す」

と覚えておきましょう。

 

はじめのうちは、どちらが消しやすいのかすぐには判断できないかもしれません。

それを解決するには、問題への慣れしかないと思います。

連立方程式に限らず、何かをできるようになるにはたくさん問題を解いて慣れるのが一番の勉強方法です。

 

引き算で消す場合

さっきまでは、連立方程式の2つの式を足して、変数を消していました。

「加減法」の「加（足し算）」の部分を使っていたわけです。

 

次は、「減（引き算）」の方を使ってみましょう。

下の問題を解いてみます。

この連立方程式は、式同士を足しても\(x\)や\(y\)が消えないことがわかりますか？

左辺同士を足すと、

\begin{align}
(x + 4y) + (x + 2y) &= x + 4y + x + 2y\\
&= 2x + 6y
\end{align}

となり、どちらの変数も残ったままです。

しかし、式同士を引き算すると、\(x\)が消えそうです。

 

では、上の式から下の式を引いてみます。

まずは、左辺同士を引き算して、

\begin{align}
(x + 4y) – (x + 2y) &= x + 4y – x – 2y\\
&= 4y – 2y\\
&= 2y
\end{align}

となり、\(x\)が消えて\(y\)だけになりました。

 

次に、右辺同士の引き算は、

$$17 – 11 = 6$$

となります。

 

よって、左辺＝右辺は、

\begin{align}
2y = 6\\
y = 3
\end{align}

です。

 

あとは、\(y=3\)をどちらかの式に代入します。ここでは、上の式（\(x + 4y =17\)）にしましょう。

\begin{align}
x + 4y &= 17\\
x + 4 \times 3 &= 17\\
x + 12 &= 17\\
x &= 5
\end{align}

これで\(x\)も求まったので、答えは、

\begin{eqnarray}
\begin{cases}
x = 5 & \\
y = 3 &
\end{cases}
\end{eqnarray}

となります。

 

このように、式同士を引き算する場合もあります。

「どうやったら一つの変数が消えそうか」

ということを意識して問題に取り組みましょう。

 

スポンサーリンク

消すためには前処理が必要な場合もある

最後に、

”変数を消すためには、前処理が必要な場合もある”

ということについて説明します。

 

これまでは、いきなり連立方程式の式同士を足したり・引いたりしていました。

しかし、それでは変数がどうやっても消えてくれない場合もあります。

例えば、次の例題をみてください。

このような問題では、このまま2つの式を足したり、引いたりしても\(x\)や\(y\)は消えませんよね。※確かめたい人は、実際に足したり引いたりしてみてください。

 

そこで、式に前処理をします。上の式に、\(2\)を掛けてみるのです。※なぜ掛ける数が\(2\)なのかは後ほど説明します。

式に何か数を掛けるときは、両辺にその数を掛けます↓

\begin{align}
(x + 2y) \times 2 = 3 \times 2\\
2x + 4y = 6
\end{align}

すると、連立方程式は次のように書き直せますね。

\begin{eqnarray}
\begin{cases}
2x + 4y = 6 & \\
2x – y = -4 &
\end{cases}
\end{eqnarray}

これであれば、上の式から下の式を引くことで\(x\)が消せそうです。

 

まずは、左辺同士を引いて、

\begin{align}
(2x + 4y) – (2x – y) &= 2x + 4y – 2x + y\\
&= 5y\\
\end{align}

となり、次に右辺同士を引いて、

$$6 – (-4) = 10$$

です。

 

よって、左辺＝右辺を計算して、\(y\)を求めると、

\begin{align}
5y &= 10\\
y &= 2\\
\end{align}

となります。

あとは、\(y=2\)を下の式（\(2x – y = -4\)）に代入して、

\begin{align}
2x – y &= -4\\
2x – 2 &= -4\\
2x &= – 2\\
x &= -1
\end{align}

よって、答えは、

\begin{eqnarray}
\begin{cases}
x = -1 & \\
y = 2 &
\end{cases}
\end{eqnarray}

となります。

 

共通の項を持つように何か数字を掛ける

このように式に何か数字を前もって掛けることで、連立方程式が解けるようになります。

そのとき、何を掛けるかというと、

上と下の式で共通の項を持つように数字を掛ける

ことがポイントです。

 

先ほどの問題は、

\begin{eqnarray}
\begin{cases}
x + 2y = 3 & \\
2x – y = -4 &
\end{cases}
\end{eqnarray}

の上の式に\(2\)を掛けて、

\begin{eqnarray}
\begin{cases}
2x + 4y = 6 & \\
2x – y = -4 &
\end{cases}
\end{eqnarray}

としましたが、「なぜ\(2\)を掛けたか」というと、\(2x\)という共通の項を作るためだったんです。

これで、上の式から下の式を引いたときにちゃんと\(x\)の項が消えるようになったのです。

 

方法は一つじゃない

先ほど、「\(2\)を掛けて\(x\)を消せるようにした」という説明をしましたが、変数を消す方法はこの方法だけではありません。

例えば、さっきの連立方程式、

\begin{eqnarray}
\begin{cases}
x + 2y = 3 & \\
2x – y = -4 &
\end{cases}
\end{eqnarray}

の下の式に\(2\)を掛けてみます。

すると、

\begin{eqnarray}
\begin{cases}
x + 2y = 3 & \\
4x – 2y = -8 &
\end{cases}
\end{eqnarray}

となります。

ここで、\(y\)の項が共通になりましたね。※ただし、今度は符号が逆です。

こうしておいて、今度は2つの式を足します。

左辺同士の足し算をしてみます↓

\begin{align}
(x + 2y) + (4x – 2y) &= x + 2y + 4x – 2y\\
&= 5x\\
\end{align}

すると、今度は\(y\)の項が消えますね。

 

右辺同士の足し算は\(3+(-8)=-5\)なので、左辺＝右辺は、

\begin{align}
5x = -5\\
&= -1\\
\end{align}

となり、あとは\(x=-1\)を上の式（\(x+2y=3\)）に代入して、

\begin{align}
x+2y &= 3\\
-1+2y &= 3\\
y &= 2\\
\end{align}

となり、\(x=-1, y=2\)という引き算で求めたときと同じ答えが得られました。

 

まとめ

ここでは、連立方程式を加減法で求める方法を説明してきました。

最後にポイントをまとめておきます。

 

加減法とは、

二つの式を足したり、引いたりして、どちらかの変数（\(x\)や\(y\)）を消す！

ことで、連立方程式を解く方法です。

消す変数は\(x\)でも\(y\)でも、どちらでもオッケーです。

 

また、”足し算で消す”場合もあれば、”引き算で消す”場合もあります。

どちらを使うべきかを判断できるように問題を解いて練習しましょう。

 

式同士の足し算・引き算をする前に前処理が必要なときもあります。

どのような数を事前に式に掛けておけば、変数が消せるかを考えましょう。

\(x\)もしくは\(y\)の前の値が同じになるように、値を掛けるのがコツです。