【中学2年数学（式の計算）】単項式の掛け算の解き方をわかりやすく解説

2019年10月10日

単項式の掛け算の基本

計算の解説を始める前に、「単項式」というのは何かをきちんとわかっていますか？

単項式とは、足し算や引き算がない文字と数字だけの式です。

このあたりに自身が無い人は、まずは以下のページで「単項式」と「多項式」の違いについて学びましょう。

 

さて、では単項式の計算の解説にはいります。

まずは、単項式同士の掛け算の意味を正しく理解しましょう。

文字が式の中にあるので、難しく感じるかもしれませんが、計算の基本的な考え方は数字だけの計算の場合とまったく同じです。

 

例えば、以下のような計算の式があったとします。

$$a \times a$$

この答えは、

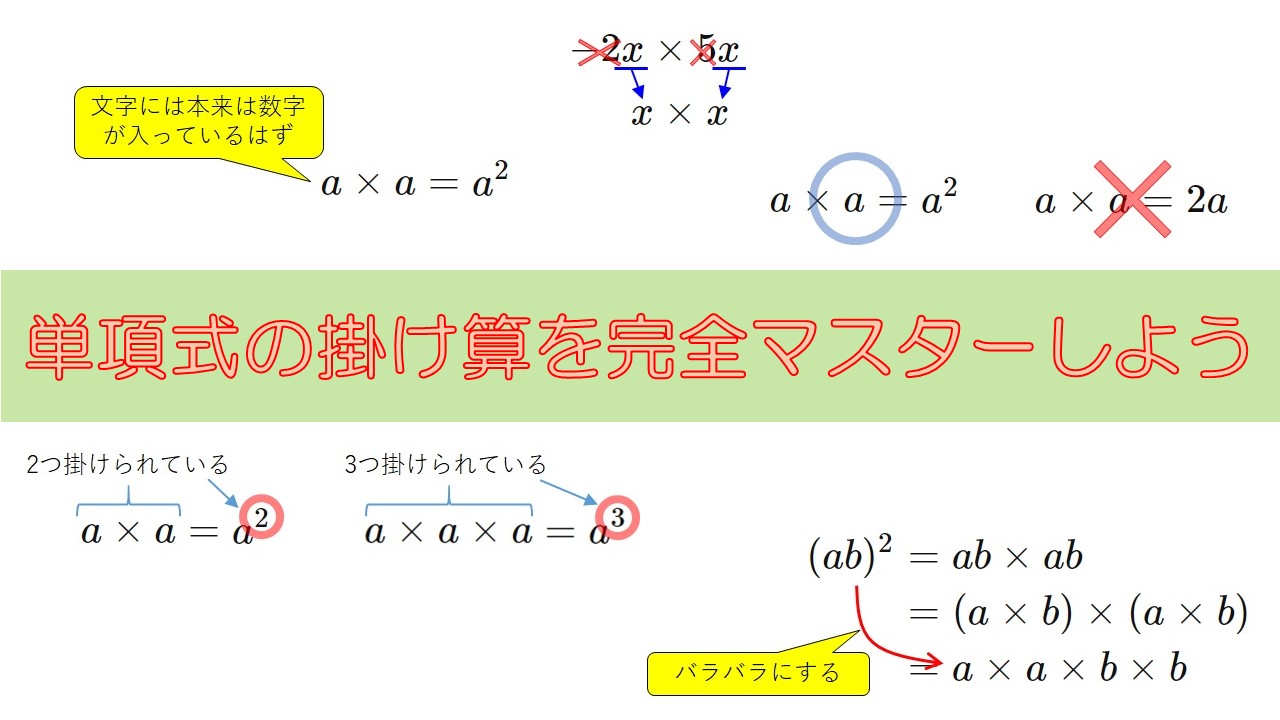
$$a \times a = a^2$$

です。

 

ここで、よくある間違いが、

$$a \times a = 2a$$

としてしまうことですね。

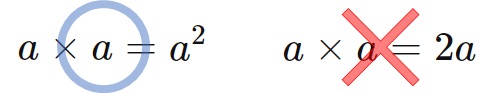
では、なぜ\(a \times a = a^2\)というように、答えは\(a\)の二乗となるのでしょうか？

それは、\(a\)に実際の数字を入れて考えるとわかります。

 

本来、文字の部分\(a\)には何か数字（値）が入っています。ただその値がわからないので、文字で置き換えているのです。

なんでもいいのですが、ここでは\(a\)に\(3\)を入れてみましょう。すると問題の掛け算は、

$$a \times a = 3 \times 3$$

となります。

 

これは簡単に解けて、答えは\(9\)ですね。

つまり、以下の式のように考えられます。

$$3 \times 3 = 3^2 = 9$$

この式の\(3\)を\(a\)に置き換えると、

$$a \times a = a^2$$

となり、\(a\)同士を掛けると\(a\)の二乗になることがわかりますよね？

 

間違った式である、

$$a \times a = 2a$$

を使ってしまうと、\(a\)に\(3\)を入れたとき、

$$3 \times 3 = 2 \times 3$$

となり、おかしなことが起こってしまいます。

\(3 \times 3\)をしたいはずなのに、\(2 \times 3\)になってしまうんですね。

 

\(a \times a\)は\(a^2\)になる！では、\(a \times a^2\)は？

$$a \times a$$

は\(a\)が2回掛け算されているので、

$$a \times a = a^2$$

となることをまずはしっかり理解するようにしましょう。

 

では、

$$a \times a^2$$

はどうでしょうか？

\(a^2\)は\(a \times a\)なので、この式は以下のような式に変形できます。

$$a \times a^2 = a \times (a \times a) = a \times a \times a$$

これは、\(a\)が3回掛け算されている式ですね。

よって、

\begin{align}
a \times a^2 &= a \times a \times a \\
&= a^3
\end{align}

となることがわかります。

 

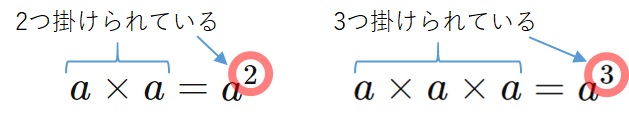
違う文字があったらどうする？（例：\((ab)^2\)）

では、違う文字があったらどうでしょうか？以下のような計算問題があったとします。

$$(ab)^2$$

 

まず、括弧の中身の\(ab\)は、

$$ab = a \times b$$

というように、\(a\)と\(b\)が掛け算されていることをまずは思い出しましょう。

 

次に、\((ab)^2\)は\(ab\)同士が掛け算されているということですから、以下のように書くことができます。

\begin{align}
(ab)^2 &= ab \times ab \\
&= (a \times b) \times (a \times b) \\
&= a \times a \times b \times b
\end{align}

 

最後は、初めにやったように、同じ文字が掛けられている数をかぞえてまとめれば完成です。

\begin{align}
(ab)^2 &= a \times a \times b \times b \\
&= a^2 b^2
\end{align}

このように、文字を含んだ数の掛け算は、一度すべてバラバラにして計算するとわかりやすいです。

慣れないうちは、面倒だと思ってもこの方法で解いてみてください。

 

数字が混ざっているとき（例：\(-2x \times 5x\)）

単項式の掛け算には、数字が混ざっていることもあります。

例えば、以下の計算を考えてみましょう。

$$-2x \times 5x$$

 

文字の前に数字がくっついています。この数字のことを「係数（けいすう）」と言います。

このように数字と文字が出てきた場合は、数字と文字を別々に計算して、最後にまとめます。

 

では、まず文字から計算してみましょう。上の計算から数字を抜かして文字だけを書くと、

$$x \times x$$

ですね。

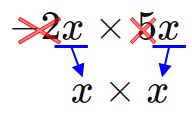
これはすでにやったように、次のように計算できます。

$$x \times x = x^2$$

 

次は、数字だけを計算して、

$$-2 \times 5 = -10$$

です。

 

最後に、数字\(-10\)と文字\(x^2\)を掛けて、

$$-10 \times x^2 = -10x^2$$

とすれば完成です。これが答えですね。

$$-2x \times 5x = -10x^2$$

 

 

スポンサーリンク

少し複雑な単項式の掛け算

では、基礎がわかったところで少しだけ複雑になった単項式の掛け算にチャレンジしてみましょう。

複雑といっても、ここまで学んだことがわかっていれば必ず解ける問題です。

 

では、問題です。

$$3ab^2 \times (-4a)$$

 

数字と文字が混ざっていますので、数字と文字を分けましょう。

$$3ab^2 \times (-4a) = (3 \times -4) \times (ab^2 \times a)$$

まずは、数字から計算すると、

$$3 \times -4 = -12$$

です。

 

次に、文字を計算すると、

\begin{align}
ab^2 \times a &= a \times b \times b \times a \\
&= (a \times a) \times (b \times b) \\
&= a^2 \times b^2 \\
&= a^2 b^2
\end{align}

です。

上の式は頭の中の計算イメージをもってもらうためにあえて長く書きましたが、計算に慣れている人は、

\begin{align}
ab^2 \times a = a^2 b^2
\end{align}

のように一気に計算してオッケーです。

 

では、数字の掛け算が\(-12\)、文字の掛け算が\(a^2b^2\)とわかりましたので、最後にまとめると、

\begin{align}
-12 \times a^2 b^2 = -12a^2 b^2
\end{align}

となり、これが答えになります。

\begin{align}
3ab^2 \times (-4a) = -12a^2 b^2
\end{align}

 

練習問題

では、最後に練習問題を解いて終わりにしましょう。

以下の単項式の計算を解いてみてください。

• \((-2x) \times 5xy^2\)
• \((-2a) \times (-3a)^2\)
• \((-\frac{2}{3})^3\)

下に答えを書きます。

 

 

• \((-2x) \times 5xy^2 = -10x^2y^2\)
• \((-2a) \times (-3a)^2 = 18a^3 \)
• \((-\frac{2}{3})^3 = -\frac{8}{27}x^3y^3\)

 

まとめ

ここでは単項式の掛け算のやり方を学びました。

 

まず、重要なのは同じ文字の掛け算は、掛けられている文字の数だけ累乗になるということでしたね。

例えば、

• \(a \times a = a^2\)
• \(x \times x \times x = x^3\)
• \(b \times b \times b \times b \times b = b^5\)

です。

 

違う文字が登場する場合は、一度すべてバラバラにして解くとわかりやすいです。

 

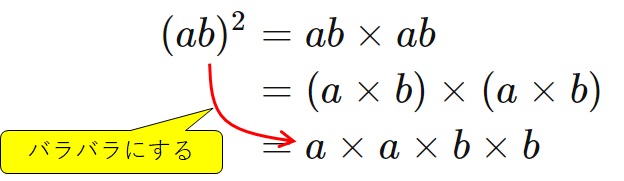
数字と文字が混ざっている計算では、数字と文字に分けてそれぞれ計算したあとに、最後にまとめてあげればオッケーでしたね。