【中学3年数学(二次関数)】平方完成のやり方をわかりやすく解説


- 平方完成のオススメのやり方を知りたい人
- 平方完成の公式が覚えられないから、できるだけ覚えなくていい方法を知りたい人
- もはや公式を使わずに平方完成したい人
平方完成のやり方について、私のオススメの方法を紹介したいと思います。
平方完成は中学の二次関数の単元で最も重要な式変形の一つですが、公式が少し複雑で覚えづらいと感じているかもしれません。
公式をなんとなくしか覚えていないと、いざテストで使用したいときにド忘れしてしまい、悲惨な結果になりかねません。
ここでは、私が一番覚えやすい・理解しやすいと思う平方完成のやり方を紹介します。
平方完成のやり方・方法
平方完成とは、以下の式変形をすることです。
$$ax^2 + bx + c = a \left( x + \frac{b}{2a} \right)^2 + c – \frac{b^2}{4a}$$
この公式を覚えてしまえばいいことなのですが、少し複雑で覚えるのは大変そうです。
なので、まずは、以下の公式を変わりに覚えましょう。
$$x^2 + bx + c = \left( x + \frac{b}{2} \right)^2 + c – \frac{b^2}{4}$$
平方完成の公式(完全版)に比べると少しだけ簡単になりました。
公式(完全版)からただ単に\(a\)が無くなっただけの式です。正確には公式(完全版)の式に\(a=1\)を代入した式となっています。
この式を覚えるときは以下のようにすればよいでしょう。
まず、\(b\)が入っている項を抜かした次の式をイメージします。
$$x^2 + bx + c = \left( x + \bigcirc \right)^2 + c – \bigtriangleup$$
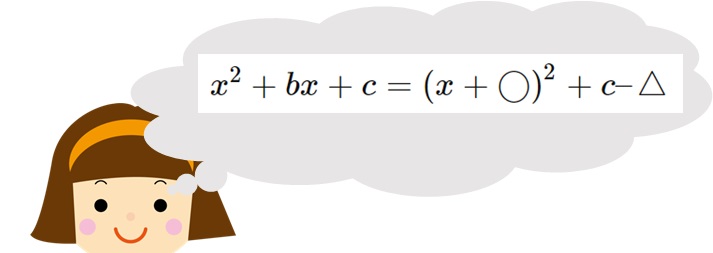
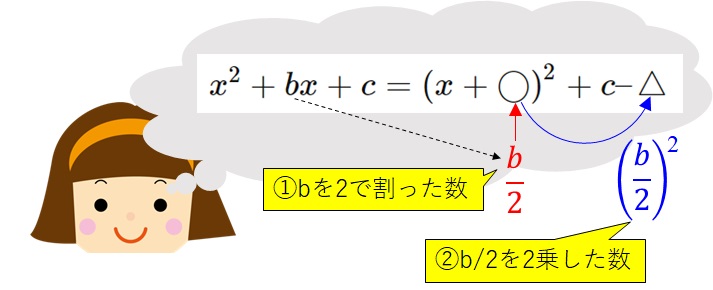
そして\(\bigcirc\)には、\(x\)の前の数字を2で割った数字(すなわち、\(b/2\))を入れます。
そして、\(\bigtriangleup\)には、\(\bigcirc\)を二乗した数(すなわち、\((b/2)^2 = b^2/4\))を入れて完成です。
$$x^2 + bx + c = \left( x + \frac{b}{2} \right)^2 + c – \frac{b^2}{4}$$
このように、覚えておけば簡単に公式を思い出せると思います。
ところで、
- 「\(a\)は考えなくていいの?」
- 「この公式じゃ、\(x^2\)の前に数字があったときに使えないでしょ」
と思うかもしれません。
しかし、大丈夫です。この公式を覚えておくだけで十分なんです。
それを実際の問題を解くことで証明してみましょう。
実際の二次関数を平方完成してみよう
この方法を使って、実際に平方完成を行ってみます。次の二次関数を考えることにしましょう。
次の二次関数を平方完成せよ。
$$3x^2 + 9x + 3$$
公式(省略版)
$$x^2 + bx + c = \left( x + \frac{b}{2} \right)^2 + c – \frac{b^2}{4}$$
を使いたいですが、問題の二次関数は\(x^2\)の前に\(3\)があるため、このままでは使えません。
なのでまずは、問題の式を以下のように変形します。
\begin{align}
3x^2 + 9x + 3 = 3 (x^2 + 3x + 1)
\end{align}
これで、右辺の( )の中の式は\(x^2\)の前に数字が無くなりました。ですので、公式(省略版)が使えます。
( )の中の式に対して公式をを使うと、\(c\)は今の場合は\(1\)なので、
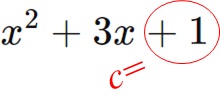
まず以下の形をイメージします。
\begin{align}
x^2 + 3x + 1 = \left( x + \bigcirc \right)^2 + 1 – \bigtriangleup
\end{align}
次に、\(\bigcirc\)は\(b=3\)の半分(3/2)が入るので、
\begin{align}
x^2 + 3x + 1 &= \left( x + \bigcirc \right)^2 + 1 – \bigtriangleup\\
&= \left( x + \frac{3}{2} \right)^2 + 1 – \bigtriangleup
\end{align}
最後に\(\bigtriangleup\)には、\(\bigcirc = 3/2\)の二乗が入るため、
\begin{align}
x^2 + 3x + 1 &= \left( x + \bigcirc \right)^2 + 1 – \bigtriangleup\\
&= \left( x + \frac{3}{2} \right)^2 + 1 – \bigtriangleup\\
&= \left( x + \frac{3}{2} \right)^2 + 1 – \left(\frac{3}{2}\right)^2
\end{align}
となります。
あとは、これを計算して、
\begin{align}
x^2 + 3x + 1 &= \left( x + \bigcirc \right)^2 + 1 – \bigtriangleup\\
&= \left( x + \frac{3}{2} \right)^2 + 1 – \bigtriangleup\\
&= \left( x + \frac{3}{2} \right)^2 + 1 – \left(\frac{3}{2}\right)^2\\
&= \left( x + \frac{3}{2} \right)^2 – \frac{5}{4}
\end{align}
となります。
そして、忘れてはいけないのが、最後に括弧の外に出していた\(3\)を掛けるという操作です。
\begin{align}
3( x^2 + 3x + 1) &= 3\left\{ \left( x + \frac{3}{2} \right)^2 – \frac{5}{4} \right\}\\
&= 3 \left( x + \frac{3}{2} \right)^2 – \frac{15}{4}
\end{align}
これで平方完成できました。
ここでは、公式(省略版)である、
$$x^2 + bx + c = \left( x + \frac{b}{2} \right)^2 + c – \frac{b^2}{4}$$
を使用しました。
このように、公式をそのままでは使えない場合(\(x^2\)の前に数字がある場合)は、初めにその数で式をくくってしまえば公式を使えるようになります。
最後にくくった数を式全体に掛けて終わりです。
スポンサーリンク
公式(完全版)の答えと比較
$$ax^2 + bx + c = a \left( x + \frac{b}{2a} \right)^2 + c – \frac{b^2}{4a}$$
を使って解いた答えと比較してみましょう。
問題は、
$$3x^2 + 9x + 3$$
ですので、
\begin{align}
a = 3\\
b = 9\\
c = 3
\end{align}
です。これを上の公式に入れると、
\begin{align}
ax^2 + bx + c &= a \left( x + \frac{b}{2a} \right)^2 + c – \frac{b^2}{4a}\\
&= 3 \left( x + \frac{9}{2 \times 3} \right)^2 + 3 – \frac{9^2}{4 \times 3}\\
&= 3 \left( x + \frac{3}{2} \right)^2 + 3 – \frac{27}{4}\\
&= 3 \left( x + \frac{3}{2} \right)^2 – \frac{15}{4}
\end{align}
となり、確かに公式(省略版)を使って解いた答えと同じになりましたね。
ここまでで、二つの公式(省略版と完全版)のやり方を紹介しました。
やはり公式(完全版)を覚えてしまうと、計算は早いですね。
どっちを使うかは、個人の自由です。自分が好きな方を使ってくださいね。私はいつも省略版を使っていました。
暗記しないで平方完成するやり方
暗記しないで平方完成するやり方を紹介します。
もはや公式を覚えたくない人もいるかもしれません。そんな人はこの方法を使ってください。
実際に以下の問題を解きながら説明します。
$$3x^2 + 9x + 3$$
まずは、\(3\)で式をくくります。これは、公式(省略版)のときと同じですね。
\begin{align}
3x^2 + 9x + 3 &= 3 (x^2 + 3x + 1)
\end{align}
次に括弧の中の式(\(x^2 + 3x + 1\))を見て、\(x\)の前の数字\(3\)を半分にした数\(3/2\)を作ります。
この数と\(x\)を足した数(\(x+\frac{3}{2}\))を作ってください。
そして、これを二乗しましょう。
\begin{align}
\left( x+\frac{3}{2} \right)^2 = x^2 + 3x + \left( \frac{3}{2} \right)^2
\end{align}

これは、問題の式(括弧の外に3を出した式)の(\(x^2 + 3x + 1\))に似ていますね。しかし、最後の項\(\left( \frac{3}{2} \right)^2\)の部分が違います。
ここからが重要です。
\begin{align}
x^2 + 3x + \left( \frac{3}{2} \right)^2
\end{align}
の最後の項をどうにかして、「\(+1\)」にすれば、元の式(\(x^2 + 3x + 1\))になるので、上の式から\(\left( \frac{3}{2} \right)^2\)を引いて、代わりに\(1\)を足してみましょう。
\begin{align}
x^2 + 3x + \left( \frac{3}{2} \right)^2 – \left( \frac{3}{2} \right)^2 + 1 = x^2 + 3x + 1 \tag{a} \label{a}
\end{align}
確かに、\(x^2 + 3x + 1\)となりました。
ここで思い出して欲しいのが、
$$x^2 + 3x + \left( \frac{3}{2} \right)^2$$
は元々、
$$\left( x+\frac{3}{2} \right)^2$$
を展開した式であったことです。
ですので、式(\ref{a})は、
\begin{align}
x^2 + 3x + \left( \frac{3}{2} \right)^2 – \left( \frac{3}{2} \right)^2 + 1 &= \left( x+\frac{3}{2} \right)^2 – \left( \frac{3}{2} \right)^2 + 1\\
&= \left( x+\frac{3}{2} \right)^2 – \frac{5}{4}
\end{align}
というように変形できることがわかります。これは、元々\(x^2 + 3x + 1\)の式でした。
なので、
\begin{align}
3x^2 + 9x + 3 &= 3 (x^2 + 3x + 1)
\end{align}
の式の右辺の\((x^2 + 3x + 1)\)を上の式に置き換えると、
\begin{align}
3x^2 + 9x + 3 &= 3 (x^2 + 3x + 1)\\
&= 3 \left\{\left( x+\frac{3}{2} \right)^2 – \frac{5}{4} \right\}\\
&= 3 \left( x+\frac{3}{2} \right)^2 – \frac{15}{4}
\end{align}
となり、答えが求まりました!
これが公式を覚えたくない人にオススメする平方完成の方法です。
ちょっと難しくてわからないなという方に向けて、簡単な問題でやってみましょう。
\(x^2\)+\(2x\)を平方完成してみます。
\((x+1)^2\)=\(x^2\)+\(2x\)+\(1\)となり、問題の\(x^2\)+\(2x\)と比べて、+\(1\)の部分が余分なので-\(1\)をします。
\(x^2\)+\(2x\)=\((x+1)^2\)-\(1\)←実際に式を計算してみると元に戻ることがわかります。
少し大きい数字にしてみましょう。
\(x^2\)+\(8x\)を平方完成してみます。
\((x+4)^2\)=\(x^2\)+\(8x\)+\(16\)となり、問題の\(x^2\)+\(8x\)と比べて、+\(16\)の部分が余分なので-\(16\)をします。
\(x^2\)+\(8x\)=\((x+4)^2\)-\(16\)←実際に式を計算してみると左の式に戻ることがわかります。
\((x+〇)^2\)で\(8x\)を作りたいので、〇の部分には問題の8を2で割った4が入ります。
余分な+16を消さないといけないので、4を2乗した数字の符号を変えたものが入ります。

ここまでは理解できましたか?
少し問題を難しくしてみます。
\(x^2\)-\(6x\)+\(4\)を平方完成していきます。
-6を2で割ると-3なので
\((x-3)^2\)となります。
余分な部分は\((-3)^2\)なので9をひきます。
\((x-3)^2\)-9になります。そして最後に問題文の+4を忘れずに書きます。
\(x^2\)-\(6x\)+\(4\)=\((x-3)^2\)-\(9\)+\(4\)=\((x-3)^2\)-\(5\)←実際に計算してみると答えが合っているか確認できます。
もう少し難し難しい問題の\(3x^2-6x+8\)を平方完成してみます。
まず\(3(x^2-2x)+8)\)の形にします。←必ず\(x^2\)を作り出します。最後の+8は( )に入れません。
\(3(x-1)^2)\)=\(3x^2-6x+3\)なので、余分な+3をひきます。
\(3(x-1)^2)-3+8\)←最後の+8を忘れずに書く。
計算すると\(3(x-1)^2)+5\)になります。実際に計算すると\(3x^2-6x+8\)になることがわかります。
\(3x^2-6x+8\)=\(3(x-1)^2)+5\)

最後に\(3x^2+9x+3\)を平方完成してみます。まずは\(x^2\)を作り出します。
\(3(x^2+3x)+3\)になりました。\(( )^2\)の形にします。数字の部分は3を2で割って\(\frac{3}{2}\)です。
\(3\left(x+\frac{3}{2}\right)^2-(\frac{3}{2})^2×3+3\)←余分な\((\frac{3}{2})^2×3\)を引いて、\(3\)を忘れずに足しました。( )の外を計算すれば完成です。
\(3\left(x+\frac{3}{2}\right)^2-\frac{15}{4}\)
意外に実用的で、実際の試験でも使える方法ですよ。
スポンサーリンク
まとめ
ここでは、平方完成の方法について3つの方法を紹介しました。
- 平方完成の公式(省略版)を使う方法
- 平方完成の公式(完全版)を使う方法
- 公式を使わない方法
の3つです。
三つの方法はそれぞれ特徴を持っています。
平方完成の公式(完全版)は公式を覚えるのは大変ですが、覚えてしまえば一番早く平方完成が行える方法になります。
公式(省略版)は覚える公式を簡単にする代わりに、少しだけ平方完成に手間がかかります。
公式を使わない方法は、公式を覚える必要がないですが解くための時間は一番かかってしまいます。
私は「平方完成の公式(完全版)を使う方法」を使っていますが、自分に合った方法を使えばいいでしょう。
























ディスカッション
コメント一覧
まだ、コメントがありません