【中学2年数学(確率)】場合の数を求める問題の解き方

- 「場合の数」って何?
- 中学数学の場合の数を求める問題の解き方をわかりやすく教えてほしい
このページでは、「場合の数」について丁寧な解説を行っていきます。
場合の数は、中学数学の確率の単元で一番はじめに登場しますね。
そして、その後に習う確率を理解するためには、場合の数をマスターすることが必須条件です。「場合の数を制するものは、確率を制す」とまで言ってしまってもいいです。
そのくらい大事なことなので、ここで説明することは必ず100%わかるようになっておきましょう。
後半には、場合の数を求める基本的な問題も出題していますので、「どのような問題が出題されるのか」「どのように解けばいいのか」を確認しましょう。
「場合の数(ばあいのかず)」とは?
場合の数とは
まず、「場合の数」とは何?から説明していきます。
ある参考書では、以下のような表現をしています。
ある事柄の起こり方が全部で\(n\)通りあるとき、その事柄の起こる場合の数は\(n\)通りであるという。
これでは少し難しいと思うので、もっとシンプルに一言で場合の数を説明すると、
それが起こるパターンがいくつあるのか
です。
教科書や市販の参考書では、これをもっとカタイ言い回しをしているので、ここで述べた場合の数の表現とは違っていますが、いっていることは同じです。
具体的に説明
簡単な例
もっと理解しやすいように、具体的な例を出していきます。
例えば、
サイコロを振ったとき、偶数の目がでる

このときの、場合の数はなんでしょう。
場合の数とは、「それが起こるパターンがいくつあるのか」でした。
いまは、「それ」というのは、「偶数の目がでる」となります。
つまり、ここでの場合の数は、
「偶数の目がでるパターンがいくつあるのか」
を考えればよいことになります。
では、考えていきましょう。言わずもがなサイコロの全部の目は1~6までです。

そのなかで、偶数の目は「2」「4」「6」の目の3つですね。
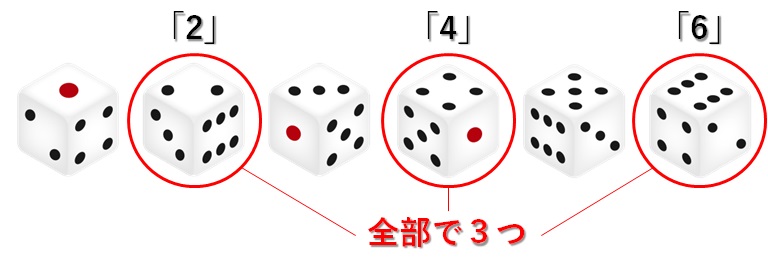
よって、「偶数の目がでるパターンがいくつあるのか」の答えは3つとなり、
サイコロを振ったとき偶数の目がでる場合の数は、\(3\)となります。
$$\text{サイコロを振ったとき偶数の目がでる場合の数} = 3$$
これが、場合の数です。具体的にイメージできましたか?
ちょっとだけ複雑な例
では、具体的な例をもう一つだけ。今後は、ちょっとだけ複雑にになります。
次の例題をみてください。
赤、青、黄色のボールがあります。これを1列に並べたときに赤のボールが先頭にくる場合の数は?
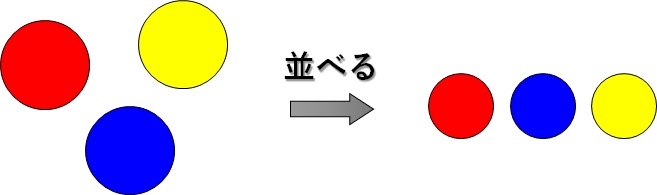
これも、「それが起こるパターンがいくつあるのか」を考えればオッケーです。
いま場合の「それ」とは、「赤のボールが先頭にくる」ですね。
ですので、「赤のボールが先頭にくるパターンがいくつあるのか」を考えます。
赤が先頭にくるパターンの並び方を考えると、
- 赤ー青ー黄色
- 赤ー黄色ー青
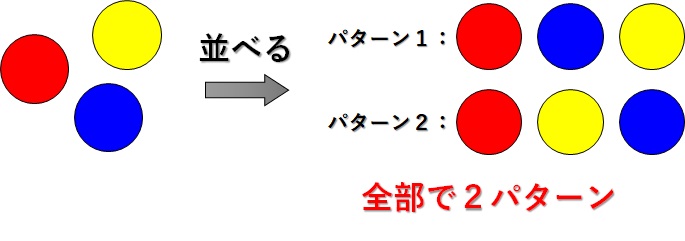
の2パターンであることがわかります。よって、
$$\text{赤のボールが先頭にくる場合の数} = 2$$
となります。
スポンサーリンク
すべての場合の数
場合の数の中でも、「すべての場合の数」というフレーズがよく登場します。
これは、そのままの意味です。
例えば先ほどの例は、「赤のボールが先頭にくる場合」でしたが、これをすべての場合の数を求める問題に変えると、
赤、青、黄色のボールがあります。これを1列に並べたとき、すべての場合の数は?
となります。
このような問題に対しては、「1列に並べるすべてのパターンについて答える」ことになります。
赤が先頭のときは、下の図に示すように2パターンでしたね↓
 並び方は他にも、
並び方は他にも、
- 青が先頭にくるパターン
- 黄色が先頭にくるパターン
がありますので、これらについても何パターンあるかを考えます。すると、
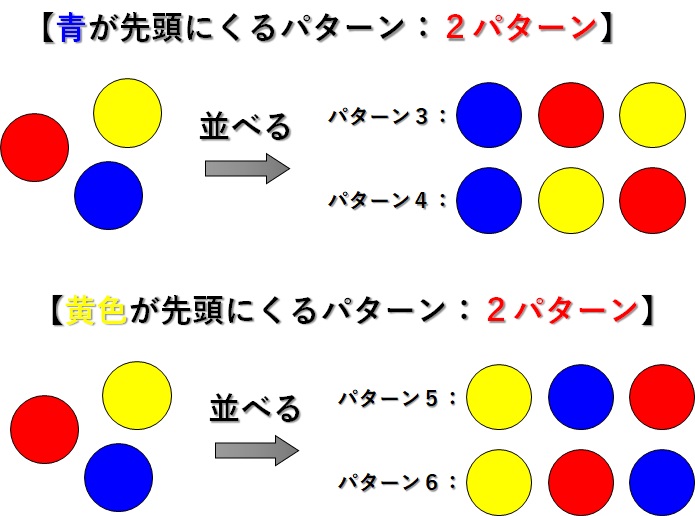
となり、
- 赤が先頭にくるパターン → 2パターン
- 青が先頭にくるパターン → 2パターン
- 黄色が先頭にくるパターン → 2パターン
の合計6パターンになります。よって、すべての場合の数は\(6\)となります。
これ以外の並びかたはありませんよね?ですから「すべて」です。
「すべての場合の数」は確率を求めるために絶対に求めることになります。必ず、その意味と次の章で紹介する求め方をマスターしておきましょう。
場合の数の問題を解いて、テクニックを習得!
場合の数とはなんなのかがわかった人は、場合の数を求める問題を解いて、より理解を深めましょう。
問題を解きながら、場合の数を求めるテクニックについても紹介していきます。ここで紹介するテクニックが使えるようになると、問題を解くのが一気に楽になりますよ。
問題は全部で3つ出題します。それぞれ違うテクニックを使って解いていきます。
樹形図(じゅけいず)で解く
第1問です。
Aさん、Bさん、Cさん、Dさんの4人がいます。この4人の中から2人を選ぶとき、その選び方は何通りあるでしょう?

この問題は「場合の数を求めよ」とは言っていませんが、やるべきことは「2人を選ぶときの場合の数を求める」ことです。
この問題を解くために紹介したいテクニックは、「樹形図(じゅけいず)」です。
下のような図を見たことはありませんか?
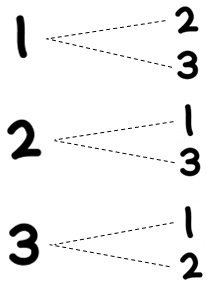
これが、樹形図と呼ばれるものです。
では、樹形図を作っていきましょう。
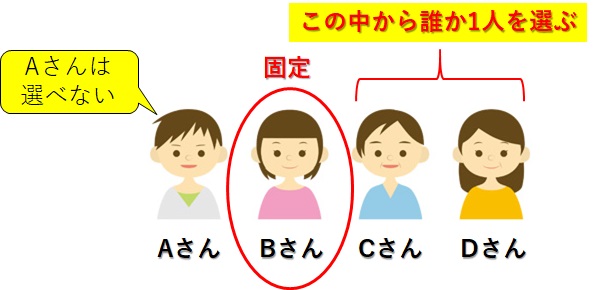
まず、4人の中からAさんが選ばれる場合を考えます。選ばれる2人のうち1人はAさんですから、残りの1人はBさん、Cさん、Dさんのうちだれか1人ということになります。
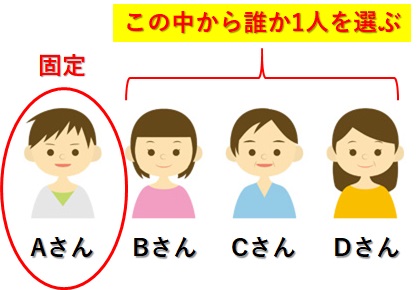
これを樹形図で表現すると、下の図のようになります↓
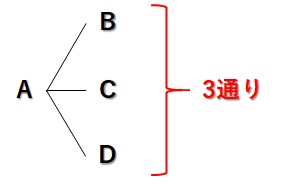
これは、3通りのパターンがあることがわかりますね。
同じように、つぎはBさんを固定した場合です。
Aさんのときと同じように、選ばれる2人のうち1人はBさんですから、残りの1人はAさん、Cさん、Dさんのうちだれか1人ということになります。
しかし、ここで注意が必要です。このときAさんを選ぶと、AさんとBさんの組み合わせになるのですが、このパターンはさきほどAさんを固定して考えたときに、すでにカウントしています。
よって、ここでは、Aさんを除外したCさんとDさんの2人からどちらかを選ぶことになります。
これを樹形図で描くと、
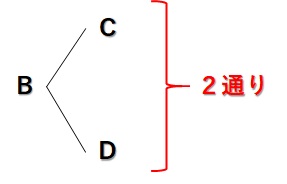
です。
次に、Cさんを固定した場合です。このときも上と同じ考えで、あと1人選べる人物はDさんしかいません。
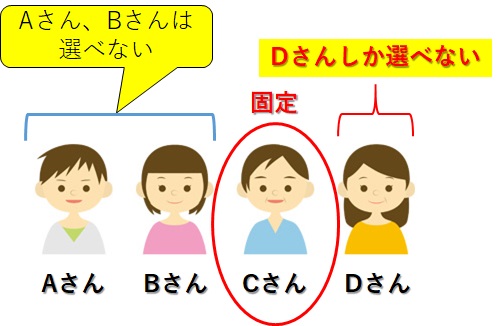
これを樹形図で描くと、

です。
最後に、Dさんを固定する場合ですが、これまでの組み合わせをみてみると、A~Cさんのどの人を選んだとしても、既にカウントしている組み合わせになっていることがわかります。

よって、もうDさんを固定する場合については考えなくてよいです。
これで、すべての場合について考え終わりました。すべての樹形図を並べてみましょう。
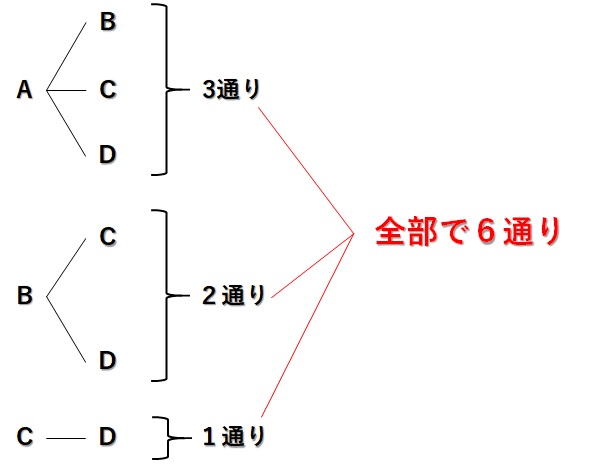
これから、すべての場合の数は\(6\)であることがわかります。
このように、樹形図はミスをせずに場合の数を数えるための協力な道具です。これは必ずマスターしておくようにしましょう。
下のページで樹形図の描き方について、説明していますのでぜひ参考にしてください↓
表で解く
第2問です。以下の例題を考えましょう。
サイコロを2回振り、二つの出た目の合計が10以上になる組み合わせは何通りでしょう。
この問題は、もちろん樹形図を描いても解けるのですが、何かを2回操作した結果を整理するときは、表を使うのが便利です。
この「2回」というのが重要です。ここではサイコロを「2回振る」という操作を行った問題なので表が使えます。
では、表を使って解いてみましょう。
まず、1回目にサイコロを振ったときの目を横に並べます。サイコロは1~6の目を持っているので、下の図のようになります↓
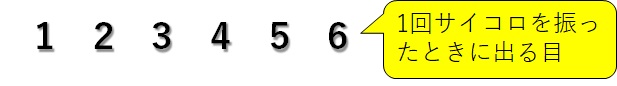
次に、2回目にサイコロを振ったときの目を縦に並べます。2回目もサイコロの目は1~6の目が出る可能性があるため、下の図のようになります↓
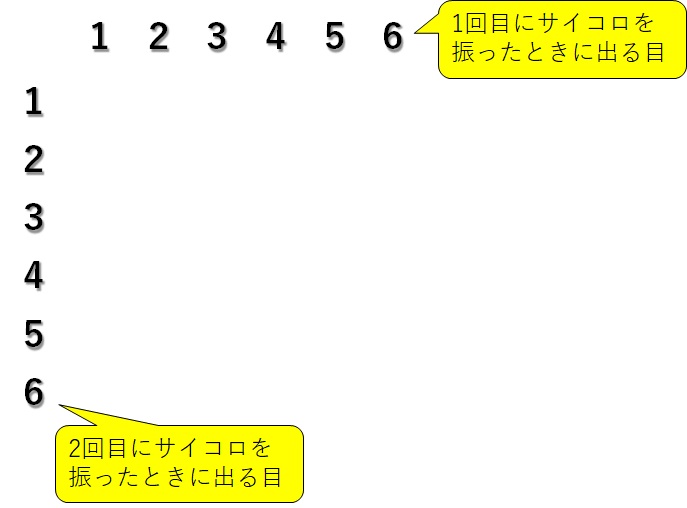
そして、ラインを引いて表にしましょう。
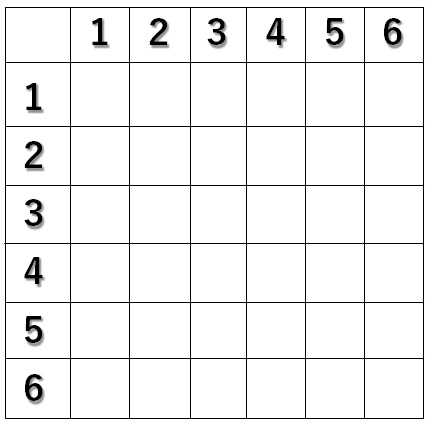
これで、表の準備は完了です。
問題をもう一度確認すると、聞かれているのは「出た目の合計が10以上になる組み合わせの数」でしたね。
なので、上の表の空きマスには、1回目と2回目のサイコロの目の合計を書き込みます↓
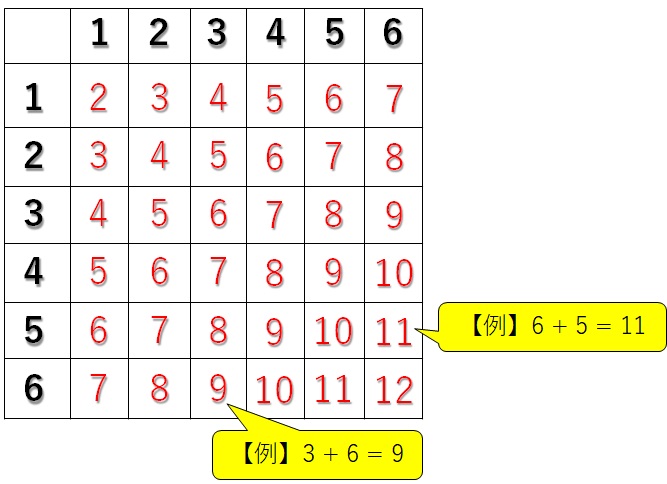
これで表は完成です。この表によって、2回サイコロを振ったときのすべての組み合わせが表現できています。
あとは、「合計が10以上」である組み合わせの数を表に書き込んだ数値から数えていけばオッケーです↓
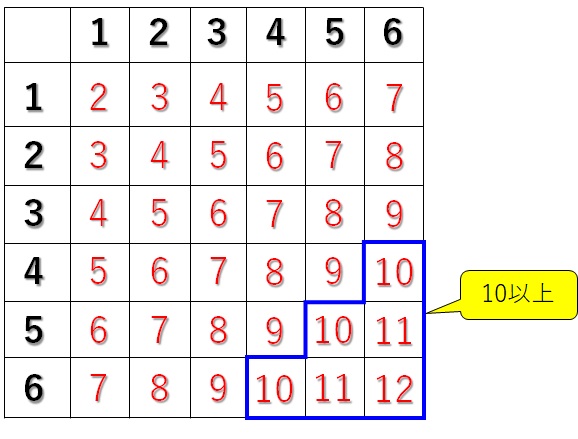
上の青い枠で囲った部分が10以上のマスです。数えると\(6\)つですね。
よって、「サイコロを2回振り、二つの出た目の合計が10以上になる組み合わせ」は、\(6\)通りということになります。これが例題②の答えです。
表を使うことで樹形図よりも簡単に、プラスわかりやすく組み合わせの数を数えることができる場合もあります。
ただし、注意すべきははじめにも述べたように、「2回の操作」を行うときの問題にしか使えません。
やってみるとわかるのですが、例題②を少し変えて、
サイコロを3回振り、二つの出た目の合計が10以上になる組み合わせは何通りでしょう。
という問題には使えません。「3回」という部分が表には不向きなんですね。
こので紹介した問題の例の他に、表が使えるパターンをいくつか紹介しましょう。
次のようなフレーズが問題に文に書かれてあるとき、表が使えます。
- 1~5番までの数字が入っているボールから2つを取り出すとき、…
- おみくじを2回引くとき、…
- A~Fさんの6人の中から2人を選ぶとき、…
これらは、何かの操作を2回行っていますね。
どのようなときに表が使えるかを判断できるようになるには、問題をたくさん解いて感覚を身につけておくことが重要です。
積の法則で解く
最後は「積(せき)の法則」というものを使って解く方法です。
積の法則とは、
①の起こる場合の数が\(N\)通りあり、そのおのおのに対して、②の起こる場合の数が\(M\)通りあるとき、
①と②がともに起こる場合の数(すべての場合の数)は、\(N \times M\)通りとなる
という法則です。はじめての人は、言葉で説明されてもピンとこないでしょうから、またまた例題を解きながら説明してきます。
以下の例題を考えてみましょう。
A町からB町をへて、C町まで行くのに、A町からB町へは\(3\)本、B町からC町へは\(4\)本の道があります。
A町からC町への行き方の組み合わせは何通りあるでしょうか?
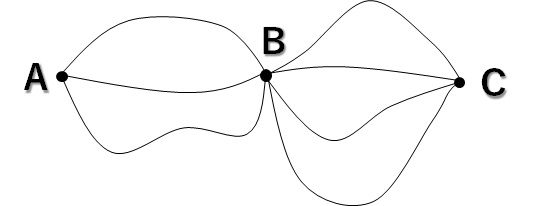
これを「積の法則」を使って解いてみます。
積の法則で、「Aの起こる場合」と「Bの起こる場合」というフレーズが出てきましたね(もう一度チェックです)↓
積の法則
①の起こる場合の数が\(N\)通りあり、そのおのおのに対して、②の起こる場合の数が\(M\)通りあるとき、
①と②がともに起こる場合の数(すべての場合の数)は、\(N \times M\)通りとなる
「①の起こる場合」という「①」をいまの問題の場合、「A町からB町に行くこと」、「②の起こる場合」という「②」を「B町からC町に行くこと」とします。
- ① → 「A町からB町に行くこと」
- ② → 「B町からC町に行くこと」
このように考えると、①が起こる場合の数と②が起こる場合の数はそれぞれ道の数だけのパターンがあるのですから、
- ① → 「A町からB町に行くこと」 → \(3\)通り
- ② → 「B町からC町に行くこと」 → \(4\)通り
となります。
「積の法則」によれば、①と②が起こる場合の数を掛け算することで、①と②がともに起こる場合の数(すべての場合の数)になるのですから、例題の「A町からC町への行き方の組み合わせは何通りあるか?」という問いに対しての答えは、
$$\text{A町からC町への行き方の組み合わせ} = 3 \times 4 = 12$$
となります。\(12\)通りというのが答えです。
樹形図を使っても解けるのに、なんで「積の法則」を使うの?
ここでは、「積の法則」を使って解きましたが、もちろんこの問題は樹形図を使っても解けます。
その場合は、経路に記号や番号をつけて道に名前を持たせ、↓
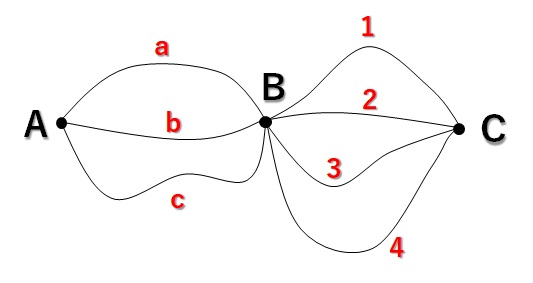
あとは、A町からB町に行く道を描き、それらそれぞれに対してB町からC町にいく道を書けば樹形図の完成です↓
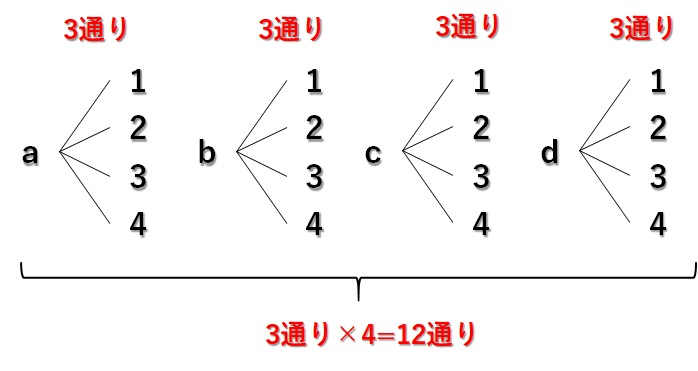
組み合わせの数を数えると、ちゃんと\(12\)通りとなっており積の法則で解いた場合と一致していますね。
では、なぜ樹形図でも解ける問題を「積の法則」で解くのでしょうか?
それは、一つには解くスピードが早いからです。樹形図を描いた人はわかると思いますが、樹形図を描くのは結構大変です。
一方、「積の法則」を使えれば、簡単な掛け算をするだけで答えが出ます。便利ですよね。
ただし、注意も必要です。きちんと問題を理解して、
- どの数とどの数を掛ければいいのか?(言い換えると、積の法則の①と②は何なのか?)
- そもそもこれは積の法則を使っていい問題なのか?
を見極めなければ使いこなすことはできません。何となく問題に出てきた数同士を掛けていては正しい答えは出てきません。
積の法則を使う二つ目のメリットは、「樹形図が描けない場合でも使える」です。
樹形図が描けない場合といっても、そのような問題はほとんどいっていいほどゼロです。
しかし、描くのが大変すぎて現実的に描くことが不可能な場合はあります。
例えば、先ほどのA町からB町をへてC町に行く問題が、次のような問題であったらどうでしょうか?
A町からB町をへて、C町まで行くのに、A町からB町へは\(12\)本、B町からC町へは\(34\)本の道があります。
A町からC町への行き方の組み合わせは何通りあるでしょうか?
頑張れば、樹形図を描けないこともないかもしれませんね。
しかし、樹形図を描き終わったころには、テスト時間は終わっているでしょう。
こんなとき、積の法則であれば、簡単な掛け算、
$$12 \time 34 = 408$$
をするだけで答えがでます。
スポンサーリンク
まとめ
ここでは、まず「場合の数」とは何なのかについて学びました。場合の数とは、
それが起こるパターンがいくつあるのか
でしたね。
そして、「すべての場合の数」も重要ワードでした。これは、そのままの意味であり、
起こる可能性があるパターンすべての数
を表すものでした。
このページの後半では、実際に場合の数を求める問題を解きながら、場合の数に慣れていきました。
場合の数を求めるとき、解き方は3つあり、
- 樹形図で解く
- 表で解く
- 積の法則で解く
でした。
この中でもっとも重要なのは「樹形図で解く」です。
確率の問題が苦手な人は、まずは樹形図をマスターすることから始めましょう!



























ディスカッション
コメント一覧
とても分かりやすいです!!助かります。
ありがとうございました。