【中学2年数学(確率)】樹形図の書き方 – どんなときでも樹形図が描けるようになるコツ
- 樹形図とは何か?、何のために使うのか?を知りたい
- 樹形図の描き方を学びたい
- 樹形図を間違えずに描くコツを知りたい
樹形図は中学数学の場合の数や確率の分野で大活躍の便利な道具です。
この記事では「樹形図とは何か?」から「樹形図をミスせずに描くコツ」まで丁寧に解説しています。
樹形図をマスターしましょう!
【動画解説】
※記事の内容はもっと詳しい説明となっていますので、記事にも目を通してみてくださいね。
樹形図とは
樹形図って?
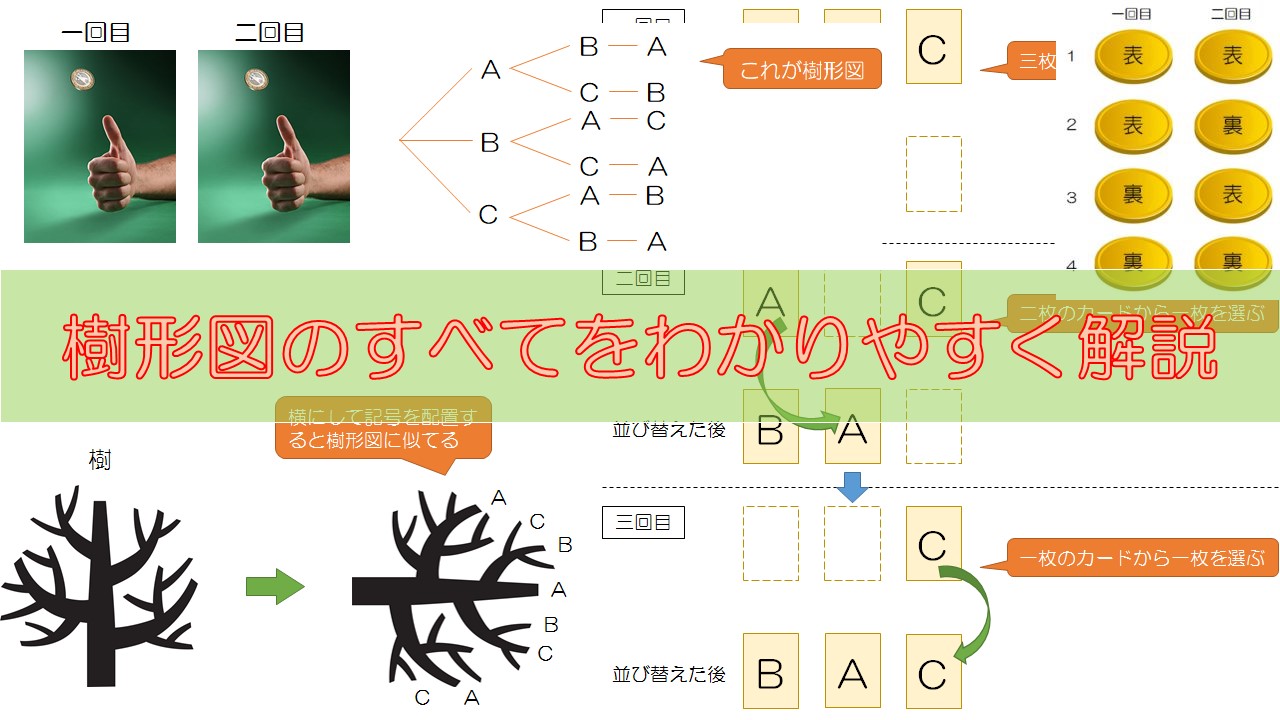
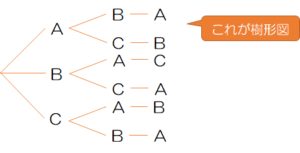
まず、樹形図(じゅけいず)とはどんなものでしょう。
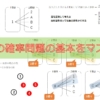
中学の確率の授業で下の画像のような図を見たことがありませんか?
これが樹形図です。
いまは、この図の意味はわからなくてもいいですよ。
ところで、なぜ樹形図という名前がついているかというと、
樹形図が樹(=木)に枝が生い茂っているような形をしているような図
だからです。
これが樹形図と呼ばれる理由ですね。
どんなとき使うの?
では、樹形図はどんなときに使われるのでしょうか?
それは、
確率の問題を解くとき、場合の数を求めるため
に使います。
またまた、”場合の数”という数学用語が出てきました。
”場合の数”というのは、例えば、コインを二回投げたときの表裏の組み合わせの数のことです。

コインには表と裏がありますが、このコインを二回連続で投げたとき、表と裏がどのような順番で出ることが考えられるでしょうか?
一つは、
一回目は表で、二回目も表

の場合がありますね。
二つ目は、
一回目は表で、二回目は裏

というパターンもあります。
さらに、
一回目が裏で、二回目は表
や
一回目は裏で、二回目も裏

というパターンもあるはずです。
これですべてのパターンを出し尽くしました。
全部で4パターンのコインの出かたが見つかりましたね。

よって、
コインを二回連続で投げたとき、すべてのパターンの”場合の数”は\(4\)通り
ということになります。
”場合の数”については、以下のページで詳しく解説していますので、そちらも参考にどうぞ。
この場合の数を知るために便利なものが樹形図なんです。
スポンサーリンク
樹形図の描き方
では、いよいよこの記事のメインである”樹形図の描き方”を学んでいきましょう。
樹形図を描くときは、次の手順で描いていきます。
- 何回”選ぶ”操作を行うのか(試行回数という)を確認する
- 一回目に選ぶことのできるすべての場合を縦に描く
- 二回目以降も考えられるすべての場合を”枝”の先へ描いていく
この3ステップの手順どおり進めていけばどんな樹形図でも必ず描くことができますよ。
実際にやっていったほうがわかりますので、次の例題を一緒に解いていきましょう。
ここに、A,B,Cと描かれたカードが三枚あります。

これを並び替えて作ることのできるカードの並びは何通りあるでしょう?
という問題があったとします。
カードを並び替えるには、三枚のカードから一枚ずつ選んでいき、左から並べていけばよいですね。
並び替え方をイラストで説明しましょう(下の画像)。
並び替え方の手順をしっかりと理解したら、樹形図を描いていきます。
もう一度、手順を確認すると、
- 何回”選ぶ”操作を行うのか(試行回数という)を確認する
- 一回目に選ぶことのできるすべての場合を縦に描く
- 二回目以降も考えられるすべての場合を”枝”の先へ描いていく
の3ステップでしたね。
まずは、
1.何回”選ぶ”操作を行うのか(試行回数という)を確認する
ですね。
これは、上のイラストでも描いているように、カードを並び替えるためには、
三回、カードを選ぶ
操作をする必要があることがわかります。
カードは全部で三枚ありますからね。
ということで、ステップ1は、
1.何回”選ぶ”操作を行うのか(試行回数という)を確認する ⇒ 三回
です。
初めのうちは、このステップ1のときに、下の図のように選ぶ回数の枠を用意しておくといいですよ。
慣れたら、この部分を描く過程は省略できるようになります。
次に、
2.一回目に選ぶことのできるすべての場合を縦に描く
をやっていきます。
一回目で選ぶことのできるのは、三枚のカードのうち一枚です。
よって、一回目に選ぶことのできるすべての場合を縦に描きましょう。
ステップ1で描いた一回目の枠の中に描きこみます。
これで、ステップ2の”一回目に選ぶことのできるすべての場合を縦に描く”はクリアです。
では、最後の”二回目以降も考えられるすべての場合を”枝”の先へ描いていく”をやっていきましょう。
まずは、自分で”枝”を描く必要があります。
”枝”とは、一つのカードから伸ばす線のことで、下の図のように描きます。
※上の図の枝の本数はデタラメに描いています。イメージだけ掴んでください。
では、一つのカードから伸ばすことのできる枝の本数を調べていきましょう。
例えば、Aから伸びる枝の本数から考えます。
一回目にAのカードを選んだときは、次に選べるカードはBかCです。
ということで、
Aから伸びる枝の本数は、二本でありその枝の先はBとC
です。
これを樹形図に描くと、
となります。
同じようにBとCについても考えていきましょう。
一回目にBのカードを選んだときは、次に選べるカードはAかCです。
また、
二回目にCのカードを選んだときは、次に選べるカードはAかBです。
よって、樹形図は下の図のように描くことができます。
続いて、三回目についても同じように考えていきましょう。
一回目でA、二回目でBとなったときの三回目のカードは何枚の中から選べるでしょう。

一回目でA、二回目でBを選んだということは、残っているカードはCだけです。
ということは、”枝”は一本でその先はCしかないということになります。
同じように、残りも必然的に描けるカードは決まっており、それらを描いていくと、

となり、樹形図の完成です。
樹形図から何がわかるのか?
樹形図は完成しましたが、この樹形図から何がわかるのでしょうか?
もう一度、完成した樹形図を見てみましょう。

この樹形図から、
A,B,Cのカードのすべての並べ方
がわかります。
樹形図を下の図のように、一行ずつに分割してみましょう。

このように、すべてのカード並べ方がわかりましたね。ぜんぶで6通りあります。
これが樹形図を描く理由の一つです。
樹形図を描くときのコツ
次に、樹形図を描くときのコツと、注意しなければいけないことを説明しましょう。
それは、
並び方は規則性(きそくせい)をもって描く(適当にバラバラにかかない)
ということです。
どいうことかを、例をだして説明します。
例えば、上で行ったA,B,Cの三枚のカードの樹形図を描くとき、
ステップ2の
”一回目に選ぶことのできるすべての場合を縦に描く”
では、

とA、B、Cの順番で描きました。
これを、
などとデタラメな順番で描いてはいけません。
あとで必ず混乱することになります。
樹形図を描くときは、はじめに自分で規則性を決めておくことが大切です。
例えば、
A → B → C
の順番で調べ、選んでいく!
と決めます。
すると、一回目の順序は、

となります。
上からA、B、Cの順になります。
次に、Aから続く二回目のカードですが、これも同じように、A、B、Cの順に考えていきます。
”Aはもう使ったから、次はBだ!”
という感じです。
もう一つの”枝”の方ですが、これもA、B、Cの順に考えて、
”Aはもう使った、Bを置きたいがこれはさっきをかぶるからダメ、じゃあCだ!”
という感じです。
次に、Bから続くカードを考えていきますが、A、B、Cの順番で考えると、
の順番になるはずです。
ここを、
としたらダメですよ。規則違反です。
このように規則を守り、樹形図を作っていくことで、ミスが減ります。
規則は自分のわかりやすいように自由に決めてオッケーです!
例えば、上の例では、
A → B → C
の順番で考えていくと決めましたが、自分が、
C → B → A
の順番のほうがわかりやすいと思えば、これでもオッケーです。
重要なことは、”自分で決めた規則を守って描く”ということです。
スポンサーリンク
樹形図を描く練習をしよう
最後に、樹形図を描く練習をしましょう。
ここまで学んだことを使って以下の例題を一緒に解いてみましょう。
ここに1円玉、5円玉、10円玉の3枚の硬貨があります。

この3枚の硬貨の並び方は何通りあるでしょうか?
では、解いていきましょう。
解き方の手順を思い出してください。
- 何回”選ぶ”操作を行うのか(試行回数という)を確認する
- 一回目に選ぶことのできるすべての場合を縦に描く
- 二回目以降も考えられるすべての場合を”枝”の先へ描いていく
の3ステップでしたね。
そして、並べるときの規則も決めておきましょう。
ここでは、
金額の大きい方から選んで並べていく
と決めます。
はじめにステップ1の、”何回選ぶ操作を行うのか”を確認します。
硬貨は3枚ありますので、並び替えるためにはこの3枚の硬貨から1枚ずつ選んで、並べていきます。
よって、”何回選ぶ操作を行うのか”の答えは3回となります。
この時点で、以下のように準備しておきましょう。
次に、ステップ2の、”一回目に選ぶことのできるすべての場合を縦に描く”です。
一回目は3枚の硬貨から1枚選ぶことになりますので、
となります。
ここで、”金額の大きい方から選んで並べる”という規則にしたがって並べているため、一番上が10円、次に5円、一番下が1円となっていることに注目です。
ステップ3です。
二回目以降も考えられるすべての場合を”枝”の先へ描いていきましょう。
二回目は、一回目で選んだ硬貨以外の2枚から選びますので、枝は2本ですね。
そして、枝の先には一回目の硬貨以外の硬貨となります。
ここでも、規則にしたがって、金額の大きな硬貨を先に選んでいます。
最後に三回目ですが、ここは残った1枚の硬貨を置くだけです。
これで完成です。
樹形図から3枚の硬貨の並び方は6通りあることがわかりました。
まとめ
お疲れ様でした。
「樹形図とは何か?」から「樹形図の描き方」と「ミスしないためのコツ」までを学びました。
ここで学んだ手順を守り作っていけば、基本的にはどんな問題でも樹形図を作ることができます。
では、最後に重要なポイントを復習して終わりましょう。
樹形図とは、”あるものを並べたときの並べ方を示すもの”です。
樹形図は、場合の数が何通りあるかを調べるときに使う便利な道具です。
樹形図は、以下の3ステップで描くことができます。
- 何回”選ぶ”操作を行うのか(試行回数という)を確認する
- 一回目に選ぶことのできるすべての場合を縦に描く
- 二回目以降も考えられるすべての場合を”枝”の先へ描いていく
ミスせずに描くコツは、
自分なりの規則を決めて描いていく
ということです。
では、また会いましょう。

























ディスカッション
コメント一覧
まだわからないです。
ピンバック & トラックバック一覧
[…] 久しぶりの樹形図を描いて3/8だ! […]