【中学2年数学（確率）】場合の数が分かれば確率が分かる
- 「場合の数ってなに？」という人
- 「求める方法はどんなものがあるの？」という人
- 「場合の数と確率はどんな関係？」という人
確率を学ぶには、必ず場合の数を学ぶ必要があります。
ここでは、そんな重要な場合の数について学んでいきましょう。
このページの内容を読み終わったとき、場合の数について「だいたい、わかった！」となっていれば、中学の確率の攻略に一歩前進です。
まずは、”だいたい”でいいですよ。最初の一歩が一番困難で重要です。
【動画解説】
※記事の内容はもっと詳しい説明となっていますので、記事にも目を通してみてくださいね。
場合の数と確率
中学数学で確率を求めるとき、場合の数を知ることがとても重要です。
場合の数を知ることは、確率を知ること
とさえ言えます。
ここでは、確率を攻略するために、絶対に必要である”場合の数”について学んでいきましょう。
スポンサーリンク
場合の数とは
場合の数とは、
ある操作を行ったとき、ある事柄が起こる場合は何通りあるか
ということです。
文章で書いてもいまいちピンとこないので、例をだして説明しましょう。
例えば、一つのサイコロがあります。
このサイコロを一回振って、2の倍数が出る”場合の数”を考えましょう。
場合の数は以下のようなものでした↓
ある操作を行ったとき、ある事柄が起こる場合は何通りあるか
この状況で、”ある操作”と”ある事柄”とは何でしょうか？
それは、”ある操作”とは”サイコロを振る”という行為、そして”ある事柄”とは”2の倍数が出る”ということです。
- ある操作：サイコロを振る
- ある事柄：2の倍数が出る
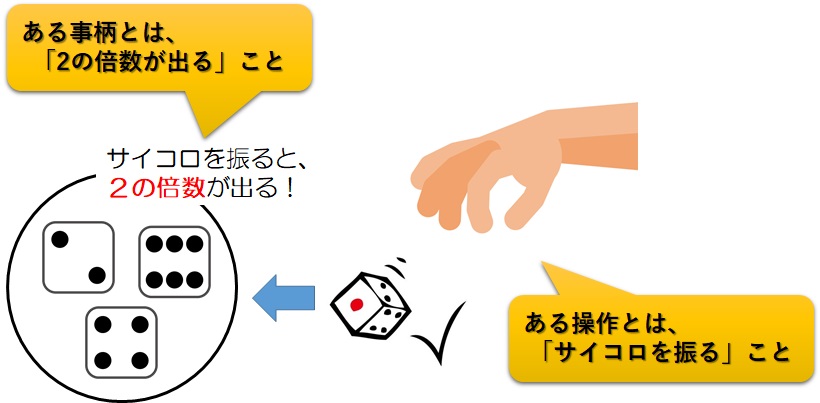
つまり、このときの場合の数を考えるときは、
サイコロを振ったとき、2の倍数の出かたは何通りあるか
を考えればいいということになります。
では、考えてみましょう。これは、簡単にわかりますね。
サイコロの目は１～６までなので、”2の倍数”は、サイコロの目の中では、2, 4, 6の3つですね。
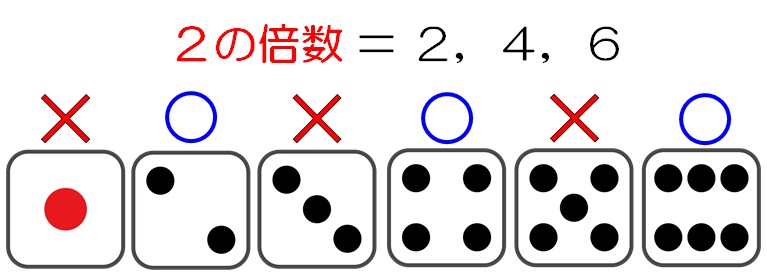
よって、”場合の数は3通り”ということになります。
どうでしょうか？場合の数がどのようなものかわかりましたか？
「まだちょっとわからない」という人へ向けてもう一つ例を出しましょう。
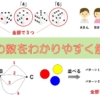
3人を並べる方法は何通り？
以下のようにAさん、Bさん、Cさんの3人がいます。
この3人を並べ替えることを考えましょう。ただし、Bさんが一番左にくるときの場合の数を求めます。
ここでもう一度、場合の数について思い出だすと、
ある操作を行ったとき、ある事柄が起こる場合は何通りあるか
でした。”ある操作”と”ある事柄”とは何でしょうか？
ここで、ある操作とは3人を並び替えること、ある事柄とは並び替えたときにBさんが一番左にくる並び方のことですね。
- ある操作：3人を並び替える
- ある事柄：Bさんが一番左にくる
よって、
3人を並び替えたとき、Bさんが一番左にくる場合は何通りであるか？
ということを考えることになります。
では、考えていきましょう。
Bさんが一番左にくるのですから、真ん中と一番右に誰がくる可能性があるかを考えます。
一つ目のパターンはAさんが真ん中にくる場合です。このときは、当然Cさんが一番右にくることになります↓
続いて、Cさんが真ん中にくるパターンもあり得ます。この場合は、Aさんが一番右にくることになります↓
その他のパターンはありませんね。よって、
3人を並び替えたとき、Bさんが一番左にくる場合は何通りであるか？
という質問に対する答えは「2通り」ということになります。
なので、このときの場合の数は2通りということになります。
場合の数の考え方をまとめる
これで、場合の数について何となくわかりましたか？
求め方についてまとめます。
まず、場合の数とは、
ある操作を行ったとき、ある事柄が起こる場合は何通りあるか
を考えることでした。
そのためには、「ある操作」と「ある事象」が何かを知る必要がありました。
ある操作とは、例えば、
- サイコロを投げる
- 並び替える
- くじを引く
などという動作になります。
次に、ある事象とは、上の操作に対して、
- 奇数の目が出る
- 最後にAがくる
- 最初にはずれを引く
という結果になります。
操作と事象を決めれば、あとはそのようになる場合は何通りあるかを数えます。
それが場合の数です。
すべての場合の数
ついでに、”すべての場合の数”についても学んでおきましょう。
これは、確率の問題で必ず必要になってくるものです。
ここまで理解できた人ならまったく難しいことではありません。
”場合の数”の前に”すべての”がついていますね。
そのままの意味で考えましょう。
つまり、”すべての場合の数”とは、
ある操作を行ったとき、起こりうるすべての場合は何通りあるか
という意味です。
ここまでは、
- サイコロの目が2である場合
- Bさんが一番左にくる場合
など、ある事象に対して条件がありました。
しかし、すべての場合の数を考えるときは、このような場合は考えません。
起こりうるすべての場合を考えるのです！
またまた、サイコロを振った場合を例として考えましょう。一度だけサイコロを振ります。
このとき、ある操作は”サイコロを振る”という行為です。
そして、この操作を行ったとき、”起こりうるすべての場合”は1～6の目のどれかが出るということですね。
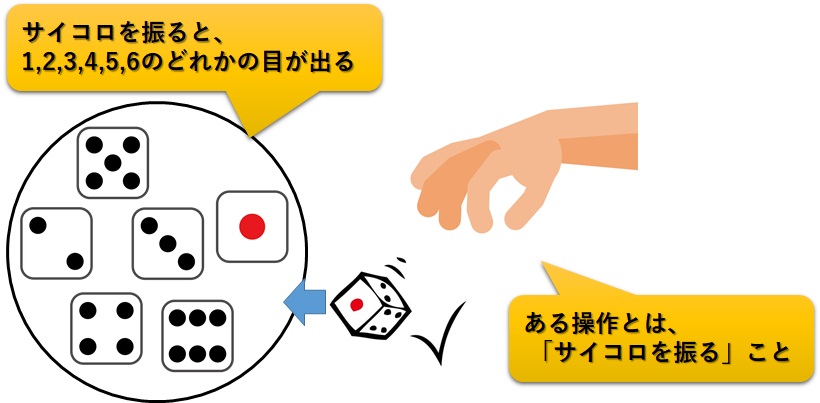
$$起こりうるすべての場合 = \text{すべてのサイコロの目}(1,2,3,4,5,6)\text{のどれかが出る}$$
ということは、”すべての場合の数は6通り”ということになります。
繰り返しますが、場合の数が
「ある場合になるのは何通りか」
を考えるのに対して、すべての場合の数は、
「すべての場合は何通りか」
を考えることになります。
この「すべての場合の数」と「場合の数」は確率も求めるために、すごく重要なことですので絶対にマスターしてくださいね。
ここまでが、場合の数について今回マスターして欲しかった内容です。
スポンサーリンク
場合の数を求める二つの方法
ここからは、おまけとして、どのように場合の数を求めるかを紹介しておきます。
中学の数学で、場合の数を求める方法は、大きく分けて二つの方法があります。
それは、
- 樹形図（じゅけいず）を描く方法
- 表を使う方法
です。
このページでこの二つの方法について分からなくても大丈夫です。
ここでは、「こんな感じの方法があるんだぁ」ぐらいの気持ちで読んでおいてください。
それぞれの詳しいページへのリンクを貼っていますので、上の2つの方法についてもっと知りたいそちらで学んでくださいね。
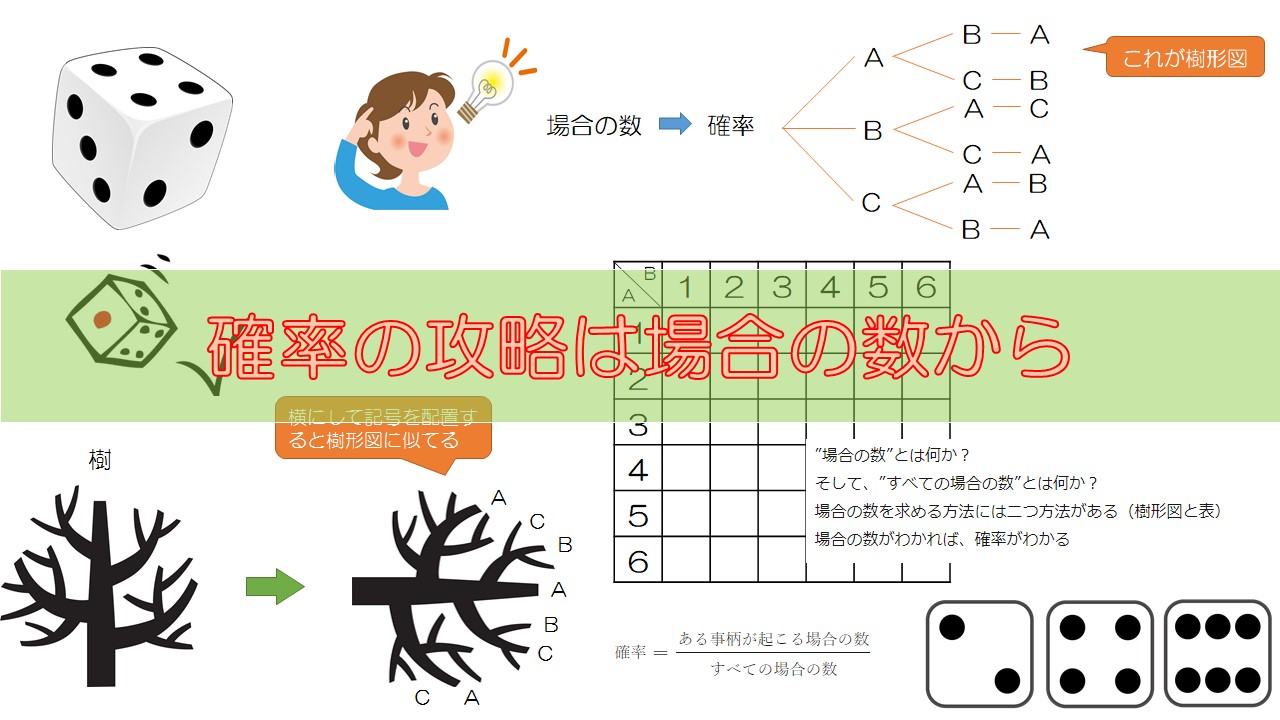
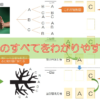
樹形図を描く方法
”樹形図（じゅけいず）”とは、下の画像のような図です。
なんだか、樹木の枝のような形をした図ですね。
なので、樹形図と呼ばれています。
この樹形図は、場合の数を求めるときに使う便利な方法です。
しかも、原理的にはどんな場合にも使える方法なので、迷ったら樹形図を使って問題を解くことになります。
樹形図に関しては、以下のページで詳しく解説しています。
https://analytics-notty.tech/how-to-write-tree-diagram/
表を使う方法
もう一つの方法は、表を使う方法です。
下のような表を描いて、場合の数を求めます。
表を使う方法は、樹形図と違って、使える場面が限られています。
しかし、使える場面ではすごくわかりやすく、そして素早く、さらにミスが少なく場合の数を求めることができる方法です。
例えば、よく表が使われる場面に、”二つのサイコロを使った確率の問題”があります。
サイコロA（1個目）とサイコロB（2個目）を振って、その出た目がある条件を満たす場合の確率を求める問題です。
このとき、表を使って”すべての場合の数”と”条件を満たす場合の数”を求めることで、簡単に確率が求まってしまいます。
下の表は、そのときに描くことになる表の例です。（意味は分からなくていいですよ。イメージだけ掴んでください。）
全部で36（=6×6）のマスがあり、その中に4つの〇がありますね。このような表から、
- すべての場合の数は36通り
- ある条件での場合の数は4通り
ということが簡単にわかる方法となっています。
表を使った場合の数を求める方法は、以下のページで詳しく解説しています。
https://analytics-notty.tech/probability-problem-with-two-dice/
場合の数がわかれば、確率もわかる
このページのはじめに、
場合の数を知ることは、確率を知ること
と言いました。
なぜ場合の数がわかれば、確率がわかるのでしょうか？
それは、確率が次の公式で求めることができるからです。
$$\text{確率} = \frac{ある事柄が起こる場合の数}{すべての場合の数}$$
公式の分子（ある事柄が起こる場合の数）も、分母（すべての場合の数）も場合の数です。
なので、場合の数が求まれば、確率もわかってしまうのですね。もう皆さんは分母と分子のどちらの意味もわかっていますよね。
では、この公式を使って一つだけ確率の問題を解いてみましょう。
例えば、一つのサイコロを振ったとします。
このとき、サイコロの目が偶数となる確率はどのくらいでしょうか？
サイコロの目は1～6までの目があり、このうち偶数は2, 4, 6の3通りです。
ですので、上の公式で、分子の”ある事柄が起こる場合の数”は\(3\)となります。
また、分母の”すべての場合の数”は、サイコロの目は6通りあるので、\(6\)です。
よって、公式に代入すると、
$$\frac{ある事柄が起こる場合の数}{すべての場合の数} = \frac{3}{6} = \frac{1}{2}$$
となりますね。
一つのサイコロを振ったとき、その目が偶数となる確率は\(\frac{1}{2}\)となります。
二つの”場合の数”を使って確率が求まりましたね。
スポンサーリンク
まとめ
ここでの目標は、
- ”場合の数”とは何か？
- そして、”すべての場合の数”とは何か？
- 場合の数を求める方法には二つ方法がある（樹形図と表）←これは何となくそんなのもあるんだぁくらいでオッケー
- 場合の数がわかれば、確率がわかる
ということを知ってもらうことでした。
目標は達成できたでしょうか？
特に、”場合の数”と”すべての場合の数”の意味は、ここでしっかりと理解しておきましょうね。
わかりにくかった部分は、下のコメント欄から質問してもらえれば、できるだけわかりやすいように答えますので、気軽にどうぞ。
では、最後に重要ポイントをまとめて終わりましょう。
”場合の数”と”すべての場合の数”は、
- 場合の数 ⇒ ある操作を行ったとき、ある条件を満たす事象が何通りあるか
- すべての場合の数 ⇒ ある操作を行ったとき、すべての事象が何通りあるか
でした。
ある操作は、なにかの動作を表す。ある事象は、操作によるある結果を表す。この2つを決めてやればあとはそのパターンを数えるだけ。
場合の数を求める方法は、
- 樹形図を描く
- 表を描く
の二通りがありました。
確率の公式は、
$$\text{確率} = \frac{ある事柄が起こる場合の数}{すべての場合の数}$$
で表せるため、場合の数がわかれば、確率もわかります。
以上、お疲れさまでした。