【中学2年数学(確率)】二つのサイコロが出てくる確率の問題を攻略しよう
- 中学数学の確率で習うサイコロの問題の解き方がイマイチわからない
- サイコロが二つ出てくる問題の解き方を知りたい
- 表を使って解く確率の問題をミスせずに、確実に解きたい
ここで紹介する内容をすべて読み終わる頃には、二つのサイコロが登場する確率の問題は、たいてい解けるようになっているはずですよ!
わからないことがあったらコメントで質問してくださいね。
【動画解説】
※記事の内容はもっと詳しい説明となっていますので、記事にも目を通してみてくださいね。
二つのサイコロが登場する確率の問題を攻略しよう
中学数学で二つのサイコロが登場する確率の問題の攻略方法を紹介しましょう。

サイコロが二つ登場する問題というのは、必ず
「二つのサイコロを振ると…」
という表現が問題文の中に出てきます。
そして、振って出たサイコロ目がどのようなパターンになるかを聞かれます。
例題としては、
二つのサイコロを振ったとき、出た目の合計が10となる確率を求めなさい
のような問題です。
スポンサーリンク
二つのサイコロのすべての目の出方の数を知ることが重要
このような問題を攻略するためには、
二つのサイコロを振ったとき、何通りの目の出方があるのか
を知っておくと、すごく問題を解くのが簡単になります。
これは、どんな問題のときも基本的には変わらないものなので、どんな問題のときでも使えます。
二つのサイコロのすべての目の出方を知るためには、表を描けばわかります。
まずは、二つのサイコロに名前を付けましょう。
これは、二つのサイコロを違うものであると区別するためであり、確率の問題を解くときの重要なポイントです。
二つのサイコロが出てきたときは、二つのサイコロは違うものとして区別しよう
名前の付け方は自分のわかりやすいように付けてよいのですが、通常はA,B,C…などアルファベット一文字を使うことが多いです。
ここでは、二つのサイコロをA、Bと呼びましょう。

例えば、Aのサイコロで”1″の目が出たときに、Bのサイコロの目は1~6までです。
つまり、

ですね。
同じように、Bのサイコロで”2″の目が出たときも、Bのサイコロの目は1~6までです。

というように、表を完成させていくと、
となります。
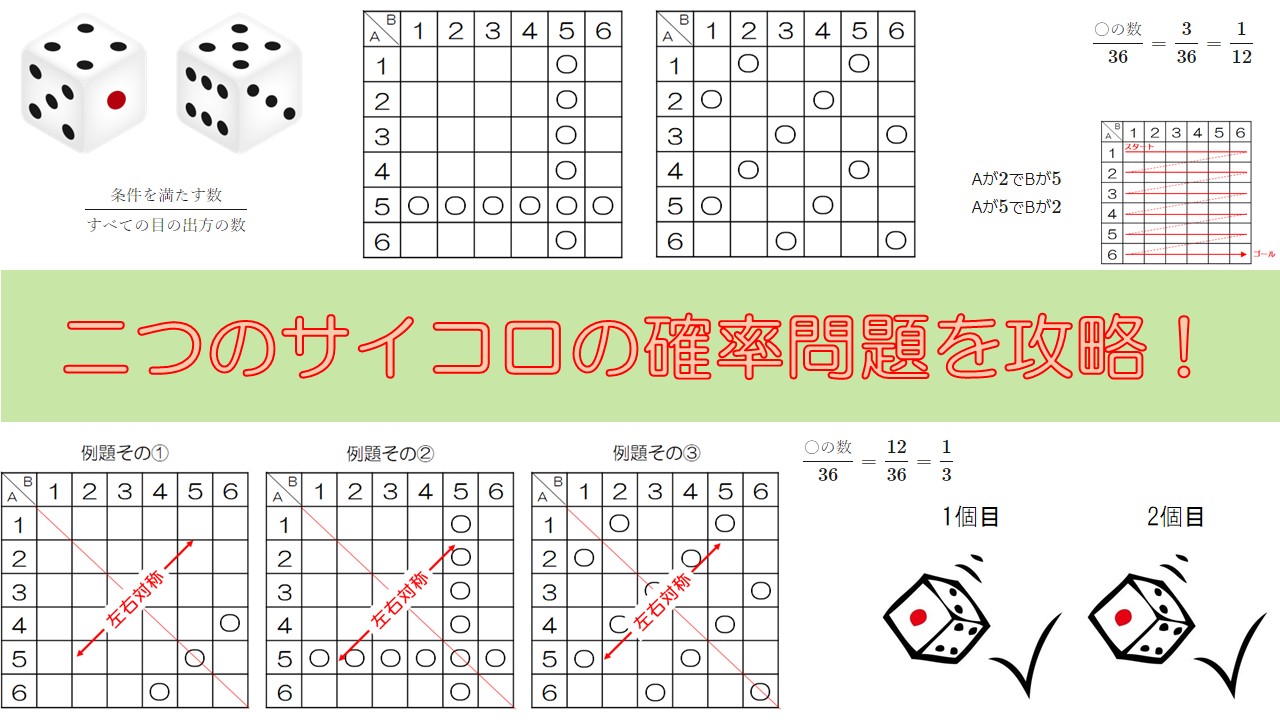
この表の見方は例えば、下の表で赤い丸が付いているマスは、
サイコロAが”5″の目で、サイコロBが”2″の目が出た
ことを表しています。
ここで、マスの数がすべての目の出方の数になりますね。
マスの数を数えていくと、全部で36あることがわかります。
よって、
二つのサイコロのすべての目の出方は36通り
であることがわかります。
この36という数字は必ず覚えておきましょう。
二つのサイコロが登場する確率の問題の解き方
二つのサイコロのすべての目の出方がわかったので、次は実際に確率の問題の解き方を学んでいきましょう。
問題を解くときの手順は、
- 表を描く
- 問題の条件を満たす場所に〇を付けて、〇の数を数える
- 分数の
\begin{align}
\frac{\text{〇の数}}{36}
\end{align}
を計算する(これが答え)
の3ステップで解いていきます。
ステップ3の”\(36\)”という数は、上で求めた”すべての目の出方の数”が入っています。
”〇の数”は、”条件を満たす数”なので、最終的には、
\begin{align}
\frac{\text{条件を満たす数}}{\text{すべての目の出方の数}}
\end{align}
という確率の公式を計算することになるのですね。
例題を解きながら覚えよう
例えば、次のような問題が出たとします。
二つのサイコロを振ったとき、出た目の合計が10となる確率を求めなさい
この問題を上の3ステップにしたがって解いていきましょう。
まずは、ステップ1の”表を描く”です。
これはどんな問題の場合でも、下のような表を描けばオッケーです。

続いてステップ2の”問題の条件を満たす場所に〇を付けて、〇の数を数える”です。
問題から条件は、
”出た目の合計が10となる”
であることがわかります。
したがって、サイコロAとBの出た目の合計が10となるところに〇を付けていきましょう。
すると、以下の表のようになるはずです。
3つの〇が付けられましたね。
それぞれ、
\begin{align}
6+4 &= 10 \\
5+5 &= 10 \\
4+6 &= 10
\end{align}
となる場所に〇がついています。
最後のステップです。
分数の
\begin{align}
\frac{\text{〇の数}}{36}
\end{align}
を計算する
をやっていきましょう。
”〇の数”はさっき数えたように、3つですので、それを分数の分子に入れると、
\begin{align}
\frac{\text{〇の数}}{36} = \frac{3}{36} = \frac{1}{12}
\end{align}
となりますね。
これで、すべてのステップが終わりました。
二つのサイコロを振ったとき、出た目の合計が10となる確率は、\(\frac{1}{12}\)となり答えを求めることができましたね。
解き方のステップを復習する
解き方のステップは重要ですので、もう一度復習しておきます。
二つのサイコロが登場する確率の問題の解き方は、
- 表を描く
- 問題の条件を満たす場所に〇を付けて、〇の数を数える
- 分数の
\begin{align}
\frac{\text{〇の数}}{36}
\end{align}
を計算する(これが答え)
の3ステップで解いていきます。
スポンサーリンク
練習問題を解いて解き方をマスターしよう
数学の解法をマスターするには、実際に問題を解いてみることが一番の早道です。
ここからは、二つのサイコロが登場する確率の問題を出題していきますので、ここで紹介した方法を使って解いていきましょう。
まったく難しくはないので、安心してくださいね。
例題その①
問題
二つのサイコロを振ったとき、出た目の合計が5となる確率を求めなさい
解き方
この問題は、前に例として解いた問題とほとんど一緒ですね。
前は”出た目の合計は10となる確率”でしたが、今回は5です。
では、解き方のステップにそって進めていきましょう。
まず、表を描きます。

これは、どんな問題でも一緒です。
次に、問題の条件を満たす場所に〇をつけます。
いまの問題の条件は、
”出た目の合計が5となる”
ですので、サイコロAとBの出た目の合計が5となる表のマスに〇をつけます。
このように、4つのマスに〇がつきます。
最後に、
\begin{align}
\frac{\text{〇の数}}{36}
\end{align}
の”〇の数”の部分に\(4\)を入れて、分数を約分すると、
\begin{align}
\frac{\text{〇の数}}{36} = \frac{4}{36} = \frac{1}{9}
\end{align}
となり、答えは、
$$\text{二つのサイコロを振ったとき出た目の合計が5となる確率} = \frac{1}{9}$$
となります。
どうですか?解けましたか?
わからないところがあったら、コメントしてくれればアドバイスしますので、気軽に言ってくださいね。
では、次の問題にすすみましょう。
例題その②
問題
二つのサイコロを振ったとき、出た目を掛けた数が\(5\)の倍数となる確率を求めなさい
解き方
今度は、出た目を足すのではなく、”掛ける”問題です。
しかも、掛けた数が\(5\)の倍数となるということは、
\begin{align}
5 \times 1 & = 5 \\
5 \times 2 & = 10 \\
5 \times 3 & = 15 \\
5 \times 4 & = 20
\end{align}
など、掛けたときの数が複数考えられますね。
少し、面倒ではありますが、これらについて一つずつ順番に考えていけば答えは求まります。
まずは、いつもの表を描きましょう。

続いて、掛けたときに\(5\)の倍数である\(5\), \(10\), \(15\), …の場所に〇をつけます。
まずは、\(5\)です。
掛けて\(5\)になるのは、
- Aが\(1\)でBが\(5\)
- Aが\(5\)でBが\(1\)
の2通りしかありません。
よって、
となります。
次に、掛けて\(10\)となる場合は、
- Aが\(2\)でBが\(5\)
- Aが\(5\)でBが\(2\)
の2通りです。
さらに、掛けて\(15\), \(20\), \(25\), \(30\)の場合についても同様に、表に追加していくと、
このようになります。
よくこの表をみると、サイコロAが5のときと、サイコロBが5のときの縦と横の列に〇がついていますね。
これは、よくよく問題を考えれば、当然のことです。
”\(5\)の倍数になる”というのは、
$$5 \times ?$$
もしくは、
$$? \times 5$$
となるときです。
\(?\)には、どんな数が入ってもよいので、上の表のように\(5\)と何かしらの数がかけられる場所(\(5\)の縦と横の列)に〇がついたのです。
さて、では〇の数を数えると、\(11\)であることがわかります。
よって、
\begin{align}
\frac{\text{〇の数}}{36} = \frac{11}{36}
\end{align}
となり、答えは、
$$\text{二つのサイコロを振ったとき出た目を掛けた数が\(5\)の倍数となる確率} = \frac{11}{36}$$
となります。
例題その③
問題
二つのサイコロを振ったとき、出た目を足した数が\(3\)の倍数となる確率を求めなさい
解き方
またまた、”二つのサイコロの目を足した数”に戻ります。
そして、サイコロの目の条件は、足した数が\(3\)の倍数であることです。
\(3\)の倍数は、\(3\)だけでなく、 \(6\), \(9\), \(12\)…なども含まれるということに気を付けましょう。
では、ステップ1の表を描きましょう。

次に、サイコロAとBの目を足した数が\(3\)の倍数となるマスに〇をつけていきます。
ここで、注意点です。この問題のように、
少し複雑な条件の場合は、一つ一つのマスについて順番に考えていくことが大切
です。
どうゆうことか実際に解いていきながら説明します。
まずは、下の表の矢印のマスについて考えます。
このマスはサイコロAが\(1\)、サイコロBが\(1\)なので、足した数は、
$$1 + 1 = 2$$
となり、\(2\)は\(3\)の倍数ではないですね。
なので、〇はつきません。
次に、一つ隣のマスに移動して考えます。
このマスはサイコロAが\(1\)、サイコロBが\(2\)なので、足した数は、
$$1 + 2 = 3$$
となり、\(3\)は\(3\)の倍数です。
なので、〇がつきます。
このように、一マスずつ順番に〇がつくかどうかを考えていきます。
考えるマスの順番は、ランダムに移動せずに、きちんと規則的に移動してください。
例えば、下の図のようにします。
このような順番で一つずつマスを調べていき、〇をつけると最終的に、
となります。
〇の数を数えると、\(12\)です。
よって、
\begin{align}
\frac{\text{〇の数}}{36} = \frac{12}{36} = \frac{1}{3}
\end{align}
となり、答えは、
$$\text{二つのサイコロを振ったとき出た目を足した数が\(3\)の倍数となる確率} = \frac{1}{3}$$
となります。
表の〇を付けた場所が正しいかをザっとチェックする方法
二つのサイコロが登場する確率の問題では、表に〇をつけて問題を解いていくことがわかったと思います。
なので、〇をつける場所を間違えてしまうと、間違った答えが出てきてしまいます。
そんなことにならないように、表に〇をつけた場所をチェックする方法を紹介しておきます。
このチェック方法を使えば、100%ではないですがかなりの確率で間違いに気づくことができるでしょう。
まずは、これまで上で解いてきた三つの表を見返してみましょう。
最終的に、下のような表になったと思います。
これらの表に斜めに線を引いてみます。

線を引いたとき、すべての表で、線の左右が対象となっていることに気づきます。
このように、
二つのサイコロが登場する確率の問題で、表に〇をつけるとき、斜めに引いた線に対して〇の位置は対象となる場合が多い
のです。
つまり、表を描いてみたとき、対象になっていなかったらどこか〇のつけ方を間違っている可能性がありますので、見直してみることが必要でしょう。
ただし、100%対象となるわけではないですので、あくまでも間違っている”可能性が高い”ということを覚えておいてくださいね。
スポンサーリンク
まとめ
お疲れ様でした。
ここまでたどり着いたあなたは、
二つのサイコロが登場する確率
の大抵の問題にたいしては、簡単に解けるようになっているでしょう。
あとは、ここで紹介した例題や、他の問題を復習してください。
きっと、前よりも確率が得意になっているはずです。
最後に、ここでの重要ポイントをザっと復習して終わりましょう。
二つのサイコロが登場する確率の問題は、次の3ステップで解きましたね。
- 表を描く
- 問題の条件を満たす場所に〇を付けて、〇の数を数える
- 分数の
\begin{align}
\frac{\text{〇の数}}{36}
\end{align}
を計算する(これが答え)
このステップを覚えておきましょう。
\(36\)は二つのサイコロの目のすべての組み合わせの数でした。
〇をつけた表が正しいかどうかを確認するには、
斜めの線に対して、〇の位置が対象であるかどうか
を確認することが有効でした。
では、数学を楽しんでくださいね。
























ディスカッション
コメント一覧
いい
樹木式と表の使い分けはありますか?
この問題のときは樹木式がよい表の方が確実などがありましたら教えてください