【中学3年数学(二次関数)】平方完成を使って二次方程式を解く

- 二次方程式を平方完成を使って解きたい
- 二次方程式を因数分解、解の公式以外で解きたい
- 平方完成の仕組みがよくわからないから丁寧に教えて欲しい
一般的に、二次方程式は基本的な因数分解や解の公式で解くことができます。
しかし、平方完成で求める方法もあります。
ここでは平方完成を用いて二次方程式を解く方法を丁寧に紹介しましょう。
因数分解以外の解き方 – 平方完成を使った解き方
「二次方程式を解け」
と言われたときにまず考えるのは、因数分解です。
次に、「この問題は簡単に因数分解ができないな。」と感じたときには、解の公式を使って解くことを考えましょう。

これが一般的な因数分解の問題が出てきたときの流れです。
一方で、これ以外にも解き方があるのはご存知ですか?
それは平方完成です。
ここでは、では平方完成について詳しくを学んでいきましょう。
スポンサーリンク
平方完成を使って二次関数を解く
早速ですが、以下の例題を解きながら平方完成について学んでいきましょう。
二次方程式\(x^2+2x=0\)を平方完成して解いてみよう。
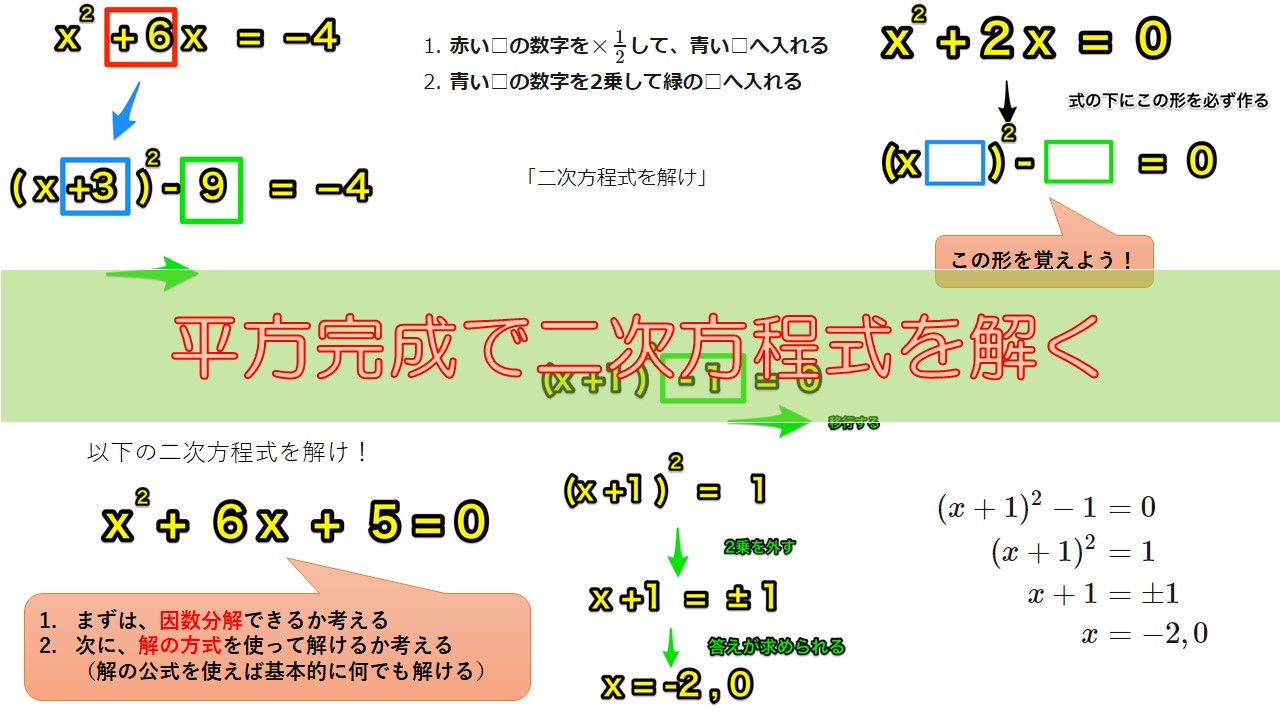
まず平方完成をするには形を覚えることが重要です。
平方完成するときは2次方程式の式の下に以下のような形を書きましょう。
平方完成はこの形を作ることから始まります。
特に、( )の後の符号はマイナスになっていることに注意しましょう。
形を作ることができたら、それぞれ四角の中に数字を入れていきます。
それぞれの四角にはどんな数字が入るのか、下の図で説明しているので見てみましょう。
まず、青い四角の中には赤い四角に入っている数字の半分を入れます。
ただし、奇数などで半分にできない場合も考えられるので、\(\times \frac{1}{2}\)すると考えておくとよりよいです。
青い四角に入る数字が求められたら、今度は青い四角の数字の2乗を緑の四角に入れましょう。
まとめると、
- 赤い□の数字を\(\times \frac{1}{2}\)して、青い□へ入れる
- 青い□の数字を2乗して緑の□へ入れる
です。
文字で説明するとややこしいので上の図で覚えると楽ですよ。
もう一度、図を示しておきます。

では、実際に数字を入れてみましょう。
いま考えている式は、
$$x^2+2x=0$$
でした。
まず、赤い四角の数字は\(2\)なので青い四角には半分の\(1\)が入ります。
次に、緑の四角に入る数字を考えましょう。
青い四角は\(1\)なので\(1\)を2乗します。
\(1^2=1\)なので、緑の四角には\(1\)が入ります。
注意点は緑の四角の前の符号はマイナス(\(-\))になることです。
間違えないようにしましょう。
\begin{align}
x^2+2x &= 0 \\
(x+1)^2-1 &= 0
\end{align}
ここまでは、理解できましたか?
この形に変形することを平方完成と言います。
では、このまま方程式を解いていきます。
\begin{align}
(x+1)^2-1 &= 0 \\
(x+1)^2 &= 1 \\
x+1 &= \pm 1 \\
x &= -2, 0
\end{align}
ですね。下の図に上式の式変形の説明を示しておきます。
上図を見てみると、はじめに、\(-1\)を右辺に移項しています。
その後、2乗を外すと、右辺の\(1\)は\(\pm 1\)になります。
あとは\(x+1\)の\(+1\)を右辺に移行すると、\(x\)の答えが求められます。
数字のみの項がある場合を解いてみよう
では、もう一問解きましょう。
今度は、以下の例題です。
二次方程式\(x^2+6x+4=0\)を平方完成を用いて解け。
例題①と同じように平方完成の形を作るのですが、今度は数字のみの項(\(+4\))があります。
このような場合は、初めに数字のみの項(\(+4\))を右辺に移項しましょう。
\begin{align}
x^2+6x+4 &= 0 \\
x^2+6x &= -4
\end{align}
右辺を移行したら、先ほどと同じように平方完成の形を作ります。
右辺が\(0\)ではないだけで、形は先ほどと一緒ですよ。
次に、青い四角には\(+6\)の半分を入れるので\(+3\)が入ります。
さらに、緑の四角には\(3\)の2乗を入れるので\(9\)が入りますね。
しつこいようですが、注意点は\(9\)の前の符号はマイナスだということです。
後の計算は、以下の通りです。
\begin{align}
(x+3)^2-9 &= -4 \\
(x+3)^2 &= 5 \\
x+3 &= \pm \sqrt{5} \\
x &= -3 \pm \sqrt{5} \\
\end{align}
よって、答えは\(x=-3 \pm \sqrt{5}\)となります。
このように、数字のみの項があっても、その項を右辺に移項してから平方完成を行うだけです。
いかがですか?
解の公式でもなく、因数分解ででもなく、平方完成で二次方程式を解くことができました。
二次関数では必須の式変形になるので、まだ覚えていない人はぜひ覚えてくださいね。
スポンサーリンク
まとめ
ここでは、平方完成を使って二次方程式の解を求めました。
二次方程式には色々な解き方があることが理解できたと思います。
解の公式を忘れてしまったときなどには、利用してみてください。
では、以下に重要なポイントをまとめて終わります。
- 平方完成は形をまずは覚えることが重要
- そのとき( )の直後の符号はマイナスになることに注意する
- 数字のみの項ははじめに右辺に移行すること























ディスカッション
コメント一覧
ちょうど分からなかったので助かりました!