【中学数学(確率)】高校入試でよく出る確率の応用問題をわかりやすく解説
この記事では、高校入試で出題された問題を紹介し、わかりやすく解説していきます。高校入試の確立の問題の出題率は非常に高いので、しっかり対策しておきましょう。
また、中学数学で出題される確率の問題のパターンはそれほど多くなく、簡単な計算しかないので少ない勉強時間で比較的点が取りやすい分野と言えるでしょう。
確率の問題を解く手順
確率の問題を解く手順は
①問題を理解する
②全事象は何通りかを考える
③全事象のうち、問題の状況は何通りかを考える
この手順で進めていけば、確率の問題は簡単に解けます。
では、さっそく問題を解いていきましょう。
高校入試レベルの問題です。
特に難しい計算や知識は必要ないので、問題文の意味が理解できれば簡単に解けるでしょう。
スポンサーリンク高校入試レベルの問題を解説
下の図のように、1辺の長さが1の正五角形ABCDEがある。点Pは最初、頂点Aにあって、1個のサイコロを投げて出た目の数だけ、正五角形の辺にそって時計回りに進み、頂点の上で止まる。サイコロを2回以上投げたときは、出た目の数の和だけ進むものとする。次の各問いに答えなさい。
(1)サイコロを1回投げたとき、点Pが頂点Bにある確率を求めなさい。
(2)サイコロを2回投げたとき、点Pが頂点Bにある確率を求めなさい。
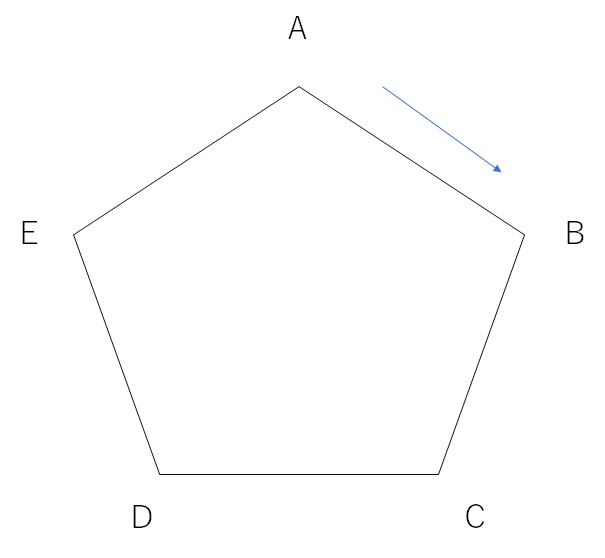
まずはどういう問題か考えてみましょう。
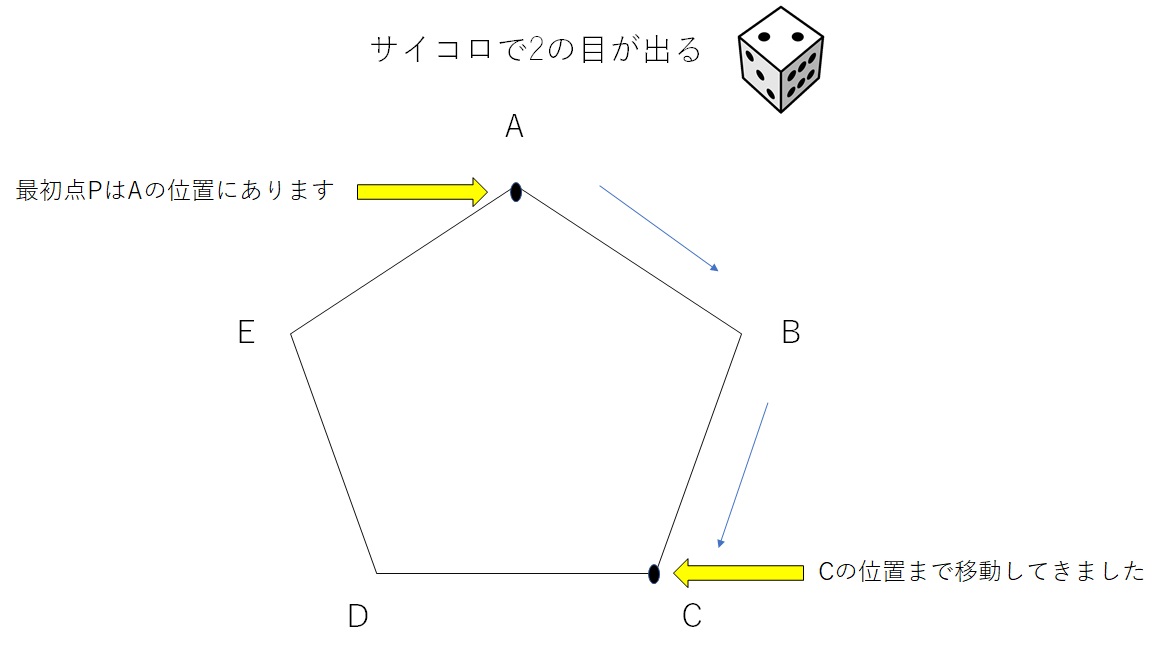
最初Pは点Aにあって、サイコロの2の目が出ると、時計回りにBを通ってCに移動します。
もう一度サイコロを投げ、出た目が3ならD、E、Aを通ってBに移動します。
サイコロの出た目の分だけ移動する問題ですね。

どういう問題かわかったので問題にとりかかっていきましょう。
(1)サイコロを1回投げたとき、点Pが頂点Bにある確率を求めなさい。
まず全事象が何通りあるか考えます。
サイコロを1回投げるので、出る目は1~6の6通りです。
6通りを全て確認して、確率を求めましょう。
出た目が1の時・・・Bの位置にあります⇒〇
出た目が2の時・・・Cの位置にあります⇒×
出た目が3の時・・・Dの位置にあります⇒×
出た目が4の時・・・Eの位置にあります⇒×
出た目が5の時・・・Aの位置にあります⇒×
出た目が6の時・・・Bの位置にあります⇒〇
出た目が1と6の時に頂点Bの位置に移動するので、確率は\(\frac{2}{6}\)となります。約分すると\(\frac{1}{3}\)です。
答え\(\frac{1}{3}\)
続いて(2)の問題です。
(2)サイコロを2回投げたとき、点Pが頂点Bにある確率を求めなさい。
まず全事象が何通りあるか考えます。
サイコロを2回投げるので、出る目は(1,1)~(6,6)の36通りです。
36通りを全て確認して、確率を求めましょう。
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6)
全事象を書きました。この中で点Pが頂点Bに移動するものは何通りか考えます。
頂点Bに移動するには、サイコロの目の和がどうなればいいでしょうか?
最初に頂点Bに移動するのは1の時です。さらに1周して6の時、さらに1周して11、16、21・・・と無限に続いていくのですが、この問題はサイコロを2回投げて出た目の和なので、6、11の時のみを考えます。
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6)
出た目の和が6になるのは、(1,5)、(2,4)、(3,3)、(4,2)、(5,1)の5通り
出た目の和が11になるのは、(5,6)、(6,5)の2通りなので、合計7通りです。
全事象は36通りなので、答えは\(\frac{7}{36}\)です。
続いてもう一問解いていきましょう。
次の問題は、円と三角形の問題なのですが、少し知識が必要です。
先ほどの問題より、難易度は高めです。挑戦してみてください。
高校入試レベルの応用問題を解説
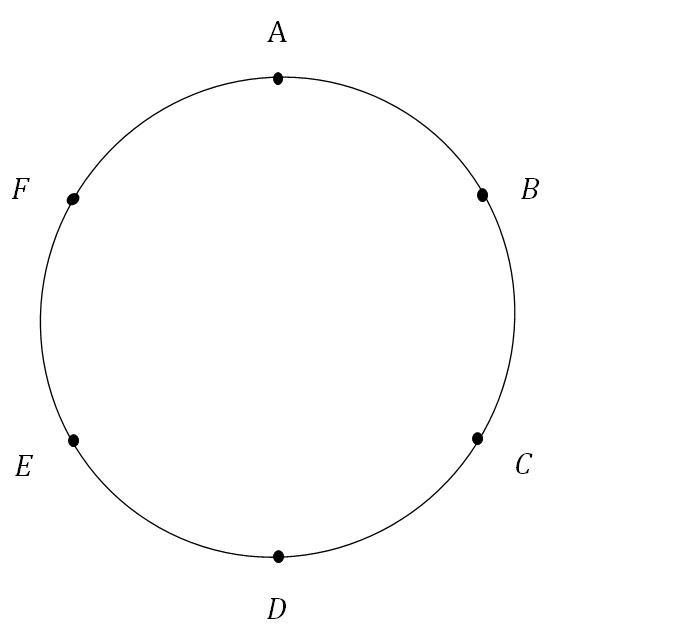
下の図において、点A、B、C、D、E、Fは1つの円の円周を6等分した点である。次の問いに答えなさい。
(1)これらの点を結んでできる弦は何本あるか求めなさい。
(2)これらの点を頂点とする三角形を作るとき、直角三角形となる確率を求めなさい。
①問題を理解する
②全事象は何通りかを考える
③全事象のうち、問題の状況は何通りかを考える
この手順で問題を解いていきましょう。まずは(1)です。
(1)これらの点を結んでできる弦は何本あるか求めなさい。
問題文の弦とは何でしょうか?
弦とは円周上の2点を結んだ線分の事です。この問題には出てきてませんが、弦とセットで弧というものも習うと思うので、きちんと覚えておきましょう。
文字だけではわかりにくいので、弦と弧を図でわかりやすくしたものを下に載せておきます。
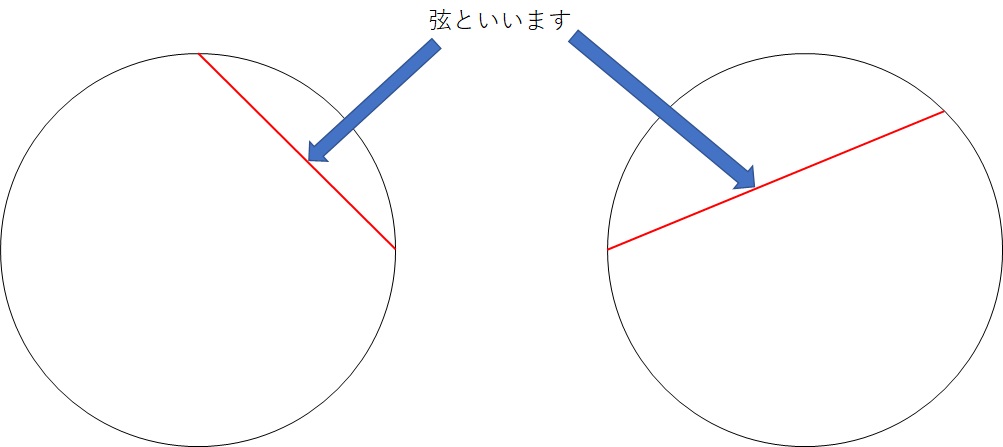
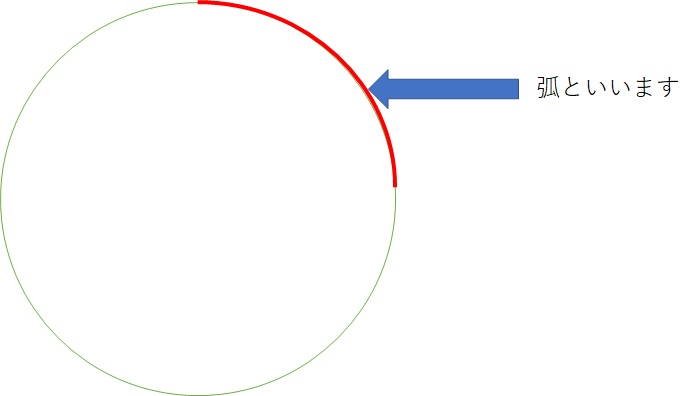
弦がどういうものかわかったところで、問題文に戻ります。
(1)これらの点を結んでできる弦は何本あるか求めなさい。
弦を全て書き出してみましょう。
AB、AC、AD、AE、AF、BC、BD、BE、BF、CD、CE、CF、DE、DF、EFの15通りですね。
答え 15通り
続いて(2)の問題です。
(2)これらの点を頂点とする三角形を作るとき、直角三角形となる確率を求めなさい。
まずは問題文を考えてみましょう。
ABC、ABDのように三角形を作っていきます。
作った三角形が直角三角形かどうかを考える問題ですね。
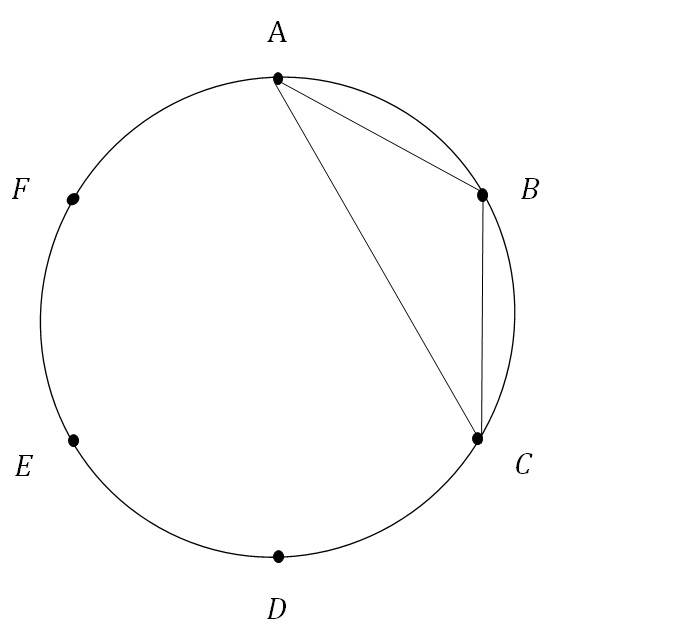
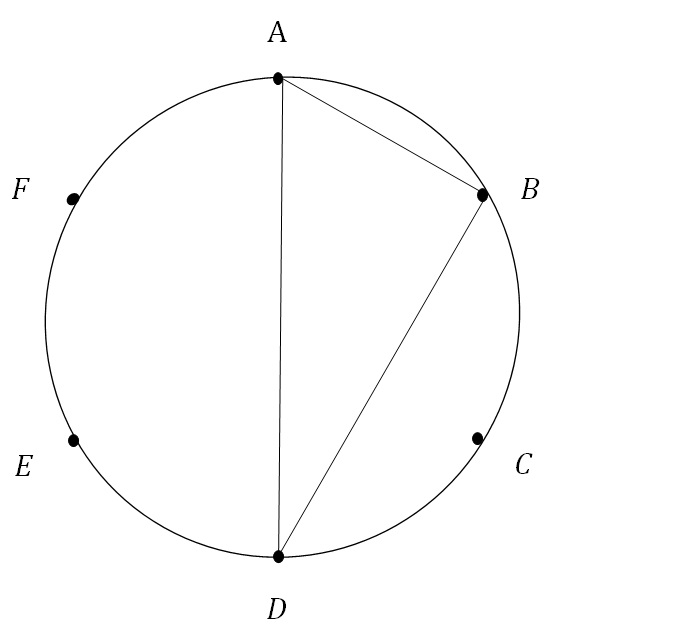
問題文が理解できたので、全事象が何通りあるか書き出してみましょう。
ABC、ABD、ABE、ABF、ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF、CDE、CDF、CEF、DEF
全事象は20通りです。この中で直角三角形になるものを探しましょう。
この問題のように、円に内接する三角形(円の中にすっぽり入る三角形)の場合、一辺が円の中心を通れば(一辺が円の直径ならば)その三角形は必ず直角三角形になります。
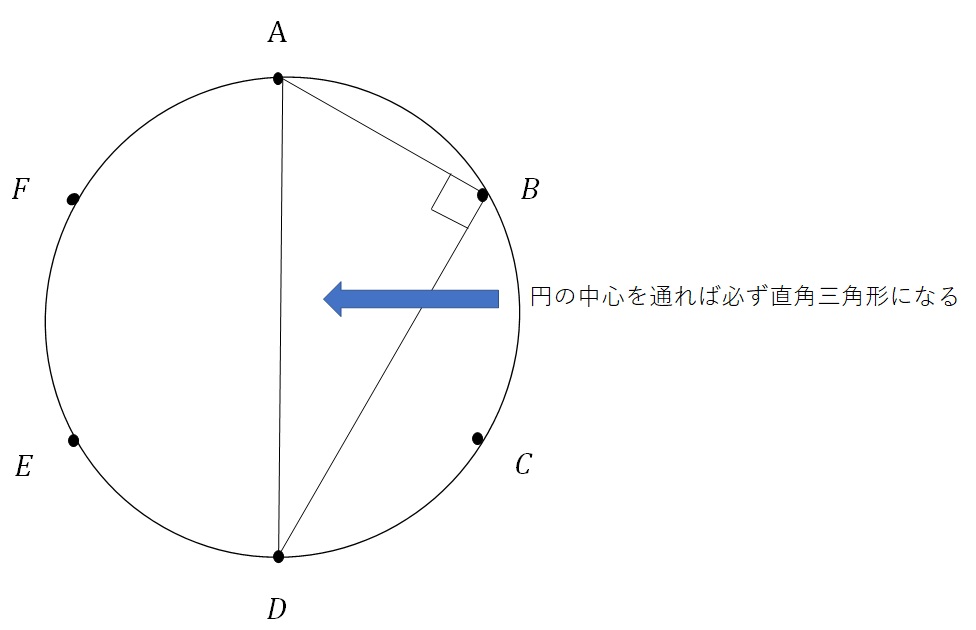
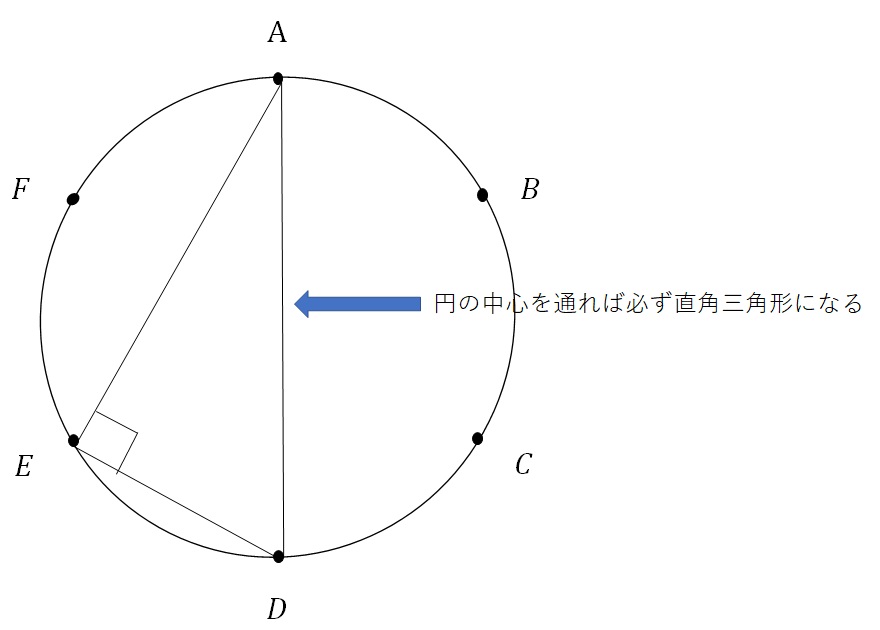
ABC、ABD、ABE、ABF、ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF、CDE、CDF、CEF、DEF
先ほど書き出したこの中から円の直径(この問題ではAD、BE、CF)を含む三角形が直角三角形になるので、いくつあるか数えます。
ABC、ABD、ABE、ABF、ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF、CDE、CDF、CEF、DEF
当てはまる三角形を赤字にしました。数えると10通りです。
全事象は10通りだったので、求める確率は\(\frac{10}{20}\)
約分すると\(\frac{1}{2}\)
答え\(\frac{1}{2}\)
スポンサーリンクまとめ
応用問題を2問解説しました。1問目は文章読解力(国語力)が問われる問題で、2問目は文章読解力+基礎知識が問われる問題だったように感じます。
数学の文章問題は国語ができないと解けないとよく言われますが、確率の問題は読解力を試される問題だと個人的に思いました。
高校数学ではより読解力や知識が必要になる問題も出てくるので、確率の問題に対する苦手意識をなくして、より難しい問題に挑戦してみてください。

























ディスカッション
コメント一覧
直角三角形となる三角形は必ずAD,BE,CFを含むものであるから、それぞれの線に対して4個づつ第三の頂点があるので12通りではないでしょうか?
ABD,ABE,ACD,ADE,ADF,BCE,BCF,BDE,BDF,BEF,CDF,CEF
12通りだとおもうのですが…
マジ卍
キチガイなのか?
12通りですね。
絶対12通り
12じゃね
6個の頂点から2個の組み合わせを求める問題なので、
6C5 =(6x5)/(2x1) = 15
6個の頂点から2個の組み合わせを求める話なので
6C5 = (6×5)/(2×1) =15
15で正解かと。
12通りで5分の3でしょ
ACDとADFを入れ忘れているので12通り
ネットには嘘の情報もあるという欠点がよくわかったと思います