モンティ・ホール問題を分かりやすく解説します – 絶対納得して欲しい!
ここでは、モンティ・ホール問題についてできるだけ分かりやすく解説していきたいと思います。
モンティ・ホール問題は問題自体は誰でも理解できるくらい簡単なものですが、その答えは数学者ですら間違ってしまうほど直観的には理解しにくいものです。
私自身、答えに納得するまでにかなり時間がかかりました。しかし、考えていくうちに必ず自分が納得できる説明にたどり着くことができると考えています。
ここを訪れてくれたみなさんが、問題を理解し答えに納得できるように問題に対する様々なアプローチの方法を丁寧に紹介していきます。
この記事を読み終わったとき、みんさんが「モンティ・ホール問題が理解できた!」と思ってくれることを目指します。
【簡単な解説動画↓】
モンティ・ホール問題を簡単に解説しました。もっと詳しい色々な説明は記事をご覧ください。
【実際にやってみた動画↓】
モンティ・ホール問題を実際にやってみました。※ルールを知らない人はまずはルールを知ってから観た方が良いと思います。
世界を震撼させたモンティ・ホール問題
”モンティ・ホール問題”とは、全米、いや世界を震撼させた数学の確率の問題です。
なぜ世界が震撼したのか?それは、
数学者じゃない普通の人にも分かるほど問題が単純なのに、数学者でも間違ってしまう
という不思議で面白い問題だったからです。
この問題は、はじめアメリカのテレビ番組で放映されました。その時の司会者をモンティ・ホール氏が務めたため、”モンティ・ホール問題”という名前がつけられています。
どんな問題なのでしょうか?
はじめに問題を紹介します。もう知っている人ももう一度確認しておきましょう。問題自体は誰でも理解できるとても簡単なものです。
モンティ・ホール問題はどんな問題?
アメリカのテレビ番組で、司会者のホール氏と挑戦者の二人がいます。※読者の方は挑戦者になったつもりで読み進めてくださいね。
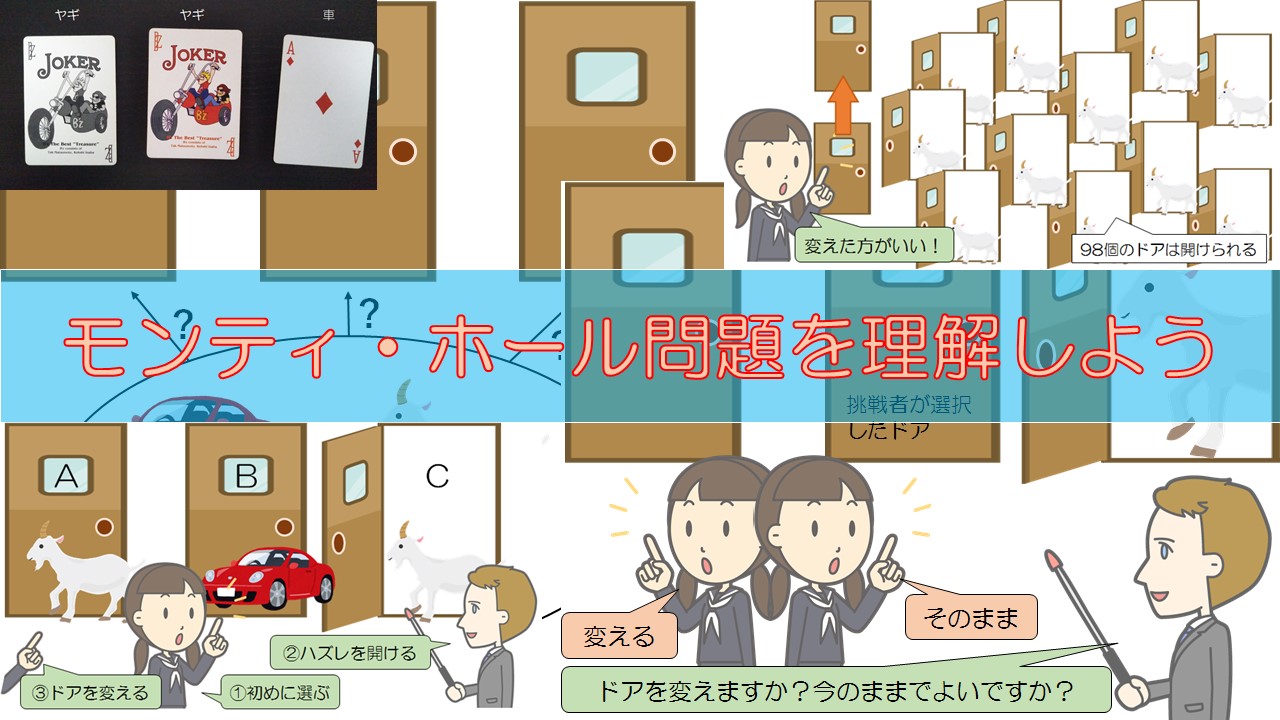
挑戦者の前に三つのドアが現れます。下の画像のようなドアです。
この三つのドアの向こう側には、車が一台とヤギは二頭のどれかがあります。ただし、どのドアの向こうに車もしくはヤギがあるかは挑戦者には分かりません。司会者のホール氏は知っています。
挑戦者はこのドアの中から一つを選んで、それが車の場合にだけその車を手に入れることができます。
まず、挑戦者は何の情報も与えられずに、一つのドアを選びます。
ここで終わりではありません。挑戦者がドアを選んだら、司会のホール氏は残り二つのドアからヤギのドア(ハズレ)を選んで開けてみせます。※必ず、ハズレを開けます。
これでハズレのドアは一つ開かれたので、車のドア(アタリ)は今挑戦者が選んでいるドアか、残りの一つのドアということになります。上の画像でいうと、一番左か真ん中のドアが当たりです。
ここで、ホール氏は挑戦者に、
「今選んでいるドアをもう一つのドアに変えますか?それとも、今のドアのままでよいですか?」
と最後の質問をします。
さて、車を手に入れるためには、挑戦者のあなたはドアを変えたほうがよいでしょうか?それとも変えなくてもよいでしょうか?
これがモンティ・ホール問題です。数学の確率の問題ですね。
正解は?
どうでしょうか?みなさんはドアを変えますか?変えませんか?
私がはじめてこの問題を知ったときは、
「ドアを変えても変えなくても確率は1/3なので、変える意味はないな」
と思いました。
だって、司会のホール氏はハズレのドアを開けた行為は、私がドアを選択した行為に何も影響を与えていないのですから、他のドアを選んだ可能性だって1/3のはずです。
ホール氏のドアを開ける行動は、何の意味もない行動であると判断したのです。
しかし、正解は、
「ドアを変えた方がよい。なぜなら、ドアを変えない場合は当たる確率が1/3なのに対して、ドアを変えると当たる確率が2/3になり二倍になるから」
です。
この問題、直感的に分かる人には分かってしまうようなのですが、私は説明を聞いてもこのようになる理由を納得できるまでかなり時間がかかりました。
みなさんはどうでしたでしょうか。
世界最高のIQの持ち主マリリンの苦悩
少し脇道にそれますが、この問題がアメリカのテレビ番組に放送されてから、マリリン・ボス・サバントという女性が、
正解は「ドアを変更する」である。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ
と雑誌のコラムに掲載しました。マリリン・ボス・サバントは、世界でもっとも知能指数(IQ)の高い人物としてギネス記録に認定されたことがある人物ですが、数学者ではありません。
前に書いたとおり、マリリンの回答は正解なのですが、世界からは彼女に対して、厳しい反論と避難の声が上がります。
その中には、かなり厳しく彼女を非難するものもいました。以下はその一部です。
- 「わたしはプロの数学者として、一般の人々の数学的知識がこんなにも低いと思っていなかった。あなた(マリリン)は自分の間違いを認める事が必要です」
- 「あなた(マリリン)は明らかに間違っている。世界最高の知能指数保有者が数学に対してこれ以上世間に無知を広める愚行を止めなさい、恥を知るように!」
こんな辛らつな内容のメッセージが彼女に寄せられたのです。しかも、このようなメッセージを送ったのは、一般の人達だけでなく大学の数学教授も少なからず含まれていました。
数学者でも間違える確率問題があるなんて不思議ですよね。しかも、その問題は一般の私たちでも簡単に理解できる単純な問題なのですから。
スポンサーリンク
モンティ・ホール問題の解説
では、モンティ・ホール問題の解説を行っていきましょう。
なぜモンティ・ホール問題の解答が、マリリンが言うように、
「ドアを変更すると当たる確率が二倍になる」
のかを詳しく説明していきます。直感的に理解するために、いくつかの異なる説明方法を紹介していきますので、どれか一つでも自分の納得できるものを探してくださいね。
解説①:始めにハズレのドアを選べば必ず最後は当たると考える
司会者のホール氏がドアを変えるか聞いたとき、
ドアを変えない場合は、当たる確率は1/3
ですね。これは、簡単に分かるでしょう。どれか一つが正解である三つのドアから一つを選ぶとき、当たる確率は当然1/3です。
ですので以下では、必ず”ドアを変える行動をとる”と決めて話を進めましょう。
始めにドアを選ぶ方法は三通りあります。まずは、下の図のようにドアに番号をつけて区別しやすくしてみましょう。
上の図は、Bのドアが当たりの場合です。挑戦者はA,B,Cのドアのどれかを選びますが、すべての場合について考えてみましょう。
まずは、Aを選んだ場合です。この場合はハズレのドアを選んでいることになります。
次に、ホール氏はもう一つのハズレのドアを開けることになります。つまりドアCです。
ここで、ドアを変えるとアタリのドアBになりますね。よって、ドアAを選んだ場合は最終的には、当たるということです。
次は、始めにBを選んだ場合です。このドアはアタリのドアです。
ホール氏がハズレのドアを開けますが、これはA,Cどちらのドアを開けるかはホール氏の気分次第ですが、どちらでもいいことです。
ここで、ドアを変えるとハズレのドアになってしまいます。よって、ドアBを選んだ場合は最終的には、ハズレるということです。

最後に、ドアCです。このドアはハズレですね。
ホール氏は、もう一つのハズレのドアAを開けることになります。
ここで、ドアを変えるとアタリのドアBとなりますね。よって、ドアCを選んだ場合は最終的に当たります。
まとめると、
- ドアAを選ぶ → 当たる
- ドアBを選ぶ → 外れる
- ドアCを選ぶ → 当たる
つまり、ハズレのドアを始めに選ぶと最終的には当たり、アタリのドアを選ぶと最終的にはハズレるということです。ハズレのドアは二つ、アタリのドアは一つなので、最終的に当たる確率は、2/3ということになります。
ドアを変えた方が変えないときの確率(1/3)より二倍高くなりますね。
これがモンティ・ホール問題の王道の解説だと思います。
解説②:司会者ホールと一緒にドアを開けると考える
次は少し考え方を変えてみましょう。分かりやすくするため、ドアに印をつけますが、あえてアタリはどのドアかは描きません。
今回も”ドアを変える行動をとる”と決めて進めていきます。
まずは、ドアAを選んだとします。そして、司会者ホール氏が残りの二つのドア(B,C)からハズレのドアを開けようとします。
でもちょっと待ってください!まだホール氏にドアを開けさせてはダメです。
このとき、自分も残ったドア(ホール氏が選んでいないB,Cのどちらか)をホール氏と同時に開けるのです。

なぜかというと、ドアを変える行動をとるということは、ホール氏がドアを開けたあと、必ずそのドアを開けることになります。なので、もう同時に開けてしまおうということです。
同時に開けるということは、”二つのドアを選んだ”という見かたもできます。つまり、ホール氏の最後の質問、
「今のドアのままでよいですか?それとも、ドアを変えますか?」
が、
「今のドアのままでよいですか?それとも、他の二つのドアにしますか?」
という意味の質問であると捉えることができるのです。
そうすると、もちろん三つの中から一つ選んだ今のドアよりも、三つの中から二つ選択できる方が確率が二倍に上がりますよね。
ホール氏の開けるドアは必ずハズレなのですが、自分が一つではなく、二つのドアを選ぶことができた(ホール氏はただの開けるだけの役)と考えると確率が二倍になるということが分かります。
どうでしょうか?わたしはこの解説がもっとも直感的に納得できました。
解説③:ハズレのドアを増やす
ハズレのドアを増やして考えてみるという方法もあります。
正式なモンティ・ホール問題では三つのドアから一つのドアを選ぶというものですが、例えば、100個のドアを使って同じ問題をやってみるのです。
すると、ゲームの進行は次のように変わります。
- 100個のドアのどれか一つにアタリがある、他すべて(99個)はハズレ
- 挑戦者は100個から一つだけドアを選ぶ
- ホール氏は残りの99個のドアから98個のハズレのドアを開けてみせる
- 挑戦者はドアを変えるか、そのままかを選択する
はじめに挑戦者は100個の中から一つのドアを選びます。このときにアタリのドアを選べる確率は1/100=1%であり、ほとんどハズレてしまいますよね。
次に、ホール氏が残りの99個のドアから98個のハズレのドアを開けてくれます。そして、ドアを変えるかどうかを質問されます。
この場合はどうでしょうか?1/100で選んだドアよりも、99個から残った一つのドアを選んだ方が当たる確率が高いということが直観的に分かりやすくなったと思います。
99個から残った一つのドアは、答えを知っているホール氏が開こうとしなかったドアなのですからね。
どうでしょうか?
実際に実験して確かめよう
実際に実験して確かめてみてもよいかもしれません。
これは、問題を理解したことにはなりませんが、実際にやってみることでゲームの内容をよりイメージできるようになります。
ゲームには司会者役と挑戦者約が必要ですので、協力者を一人連れてきてください。
本物の車とヤギを使うわけにはいきませんので、代わりにトランプを使います。トランプは三枚あれば十分です。
ジョーカーを二枚とエースを一枚準備します。ジョーカーがヤギ(ハズレ)でエースが車(アタリ)です。

では、やってみましょう。
まず、司会者がカード伏せます。このとき、挑戦者はカードを見てはいけません。
また、司会者はどのカードがジョーカーでどのカードが車かを覚えておいて下さい。

次に挑戦者はカードを選びます。

挑戦者がカード選ぶと、司会者はハズレのカード(ジョーカー)を開けます。
ハズレが二つある場合は、どちらを開けても構いません。

そして、司会者はお決まりのセリフ、
「カードを変えますか?それとも変えませんか?」
と挑戦者に尋ねます。
挑戦者は、カードを変えるか、変えないかを選び、最終的に選んだカードを開けてください。
このように、実際にゲームをやってみて、
- 必ずカードを変える
- 必ずカードを変えない
場合の二つの選択パターンをそれぞれ10回ずつやってみましょう。
勝率に差が出るはずです。
もちろん、確率の問題なのでたまたま予想外の結果が出るときもありますが、何回もやっていくとどちらの選択が当たりが出やすいかが分かるはずです。
スポンサーリンク
まとめ
- モンティ・ホール問題は誰でも理解できる確率の問題だが、数学者でも間違うことがある
- 解答を納得するには、色々な解説をみてみる
- 解説①:始めにハズレのドアを選べば必ず最後は当たると考える
- 解説②:司会者ホールと一緒にドアを開けると考える
- 解説③:ハズレのドアを増やす
- 実際にトランプでプレイしてみるとイメージがよりしやすくなる




























ディスカッション
コメント一覧
3つの扉のうち1つを回答者が選んだのだから、回答者の元に「当たり」がある確率は1/3。
3つの扉のうち2つが出題者の元に残っているので、出題者の元に「当たり」がある確率は2/3。
出題者が手元の2つのうちの「ハズレ」を1つ開示しても、出題者の元に「当たり」がある確率は変わらない。
ゆえに、出題者の手元に残っている開けていない方の扉が「当たり」の確率は2/3である。
という風に考えて見ましたが、どうでしょうか。
A君、B君、C君が それぞれカードを引いて(当たりは1枚だけ)、まずB君が開きましたらハズレでした。
そこでA君はモンティ・ホール問題を参考にして、C君と交換するとアタリの確率が1/3から2/3に倍になると考えます。
一方C君も同様にA君と交換すると確率は倍になると考えます。そこで交換成立。めでたく二人の当選確率はそれぞれ倍になりました。(えっ??)
皆さん、お分かりの通りなので、自分で突っ込み入れます。
A君,B君,C君の問題は、モンティ・ホール問題と決定的に違うとこがありますね。( ´_`)
A君 対 B,C君の 1/3 対 2/3 の確率の比をそのまま残してB君がハズレを開くのが モンティ・ホール問題でしたね。つまりB,C君がグルなんですね。どちらか一方の必ずハズレを開けるんですね。
二つの問題の比較は、モンティ・ホール問題の理解に役立ちませんかね。
それは、違うと思うけど……。モンティ氏がハズレを知っていて、最初にプレイヤーが選んでいるから、変えると確率が上がるだけで、全員知らないなら何も変わらないよ……
2018年10月12日に投稿した方。勝手に分母を削らないでください
なんか分かりにくくて、最初は、いや全然違うだろ、開示したから1つ減ったんだろ、って思ったけど、よく考えたら、間違いなく正解だと思った。
これがギャンブルなら、私なら変えない。
変える方が、当たる確率が倍になる状況を作ってまで、変えさせようとするという事は、私が当たりを選んでいるからだ。と考えます。(^_^)✌️
確率の問題でなく心理戦です。
チョットナニイッテルカワカラナイ
それな
それな
いやよくわからない
もっと単純
変えないと1/3の確立であたる
変えると最初に2/3のハズレを引いていれば必ず当たりになる(出題者が見せなかったほうを選択)
だから変えたほうが2倍あたる
全く同感です。他の説明より、簡潔で明確です。
昨日コメントをしたのですが、やり方がよくわからず再度挑戦します。
9月25日の匿名さんの考え方のほうが、上の説明よりすっきりしていてわかりやすいです。色々と場合わけするより、この8行の方が素晴らしい!
間違っていると思います…
この理論が当てはまるのは4枚以上から。
3枚のときは1枚が空いた時点で、残り2枚の確率は同様に上がる。
4枚以上から、全ての扉の枚数に比例して、選んでない方の扉の確率がより上がる。
100枚の説明でわかりやすいでしょ?じゃあ、3枚の時もそうだよね?っていう詐欺理論。
『二度目の選択時にハズレのドアを選ばないものとする』という前提が隠れているのと『1/3が1/2になるから変えるべき』という分かり易い解が一見隠れているように見えるのでややこしくなるのでは。
壺算と言う小噺もありますが文章題は数字以外の要素が絡むので面白いですね。
私は『正解する確率は最初から最後まで1/2若しくは1/3のどちらか』派です。
出題者がハズレのドアを一枚開けるという前提条件から『実は最初から二択』と考える事もできるので。
なるほど^q^
なるほどは目上の人に使うのはよろしくないですよ。
当(A,B,C)=(a,b,c)
a+b+c=1
P(当A|選A,開C)=a/(a+2b) は必ずしも (a) と一致するとは限らない
P(当B|選A,開C)=2b/(a+2b) は必ずしも (b+c) と一致するとは限らない
一致するための条件は
a=a/(a+2b)
1=1/(a+2b)
a+2b=1
2b=1-a
2b=b+c (∵a+b+c=1)
b=c
最初の投稿者です。
数学の問題に対する考え方としては邪道かもしれませんが、この問題の場合、各扉のアタリの確率よりも、
出題者と回答者の「両者それぞれがアタリを手にしている確率」に着目した方が直感的に理解しやすいのでは。
と考えたのが最初の投稿です。
上の投稿の続きです。
こういう説明ではどうでしょう。
出題者Aと回答者Bがテーブルを挟んで相対して座り、Aが箱を3個テーブル上に並べます。
Bが1個選んで手元に引き寄せ、同時にAが残った2個を手元に引き寄せるとします。
この時点でBから見ればAの方にアタリがある確率は自分の2倍であることが直感的に判りませんでしょうか。
その上でアタリがどれかを知っているAが手元の2個のうち1個を「これはハズレである」と開けて見せるのですからAの残りの1個がアタリの確率はBの手元の1個の2倍であることになります。
上でも書きましたが、扉個々のアタリの確率にこだわるために、かえって複雑になっているような気がします。
数学の問題への回答としてはどうなのかな、という気はしますが。
この問題の前提条件を踏まえて、
A.B.Cのうち当たりをAとすると…
選択肢を変えない場合に当たりを引けるのは、最初にAを選択した時だけ。
選択肢を変える場合に当たりを引けるのは、最初にAを選択しなかった(BかCを選択した)時。
なので選択肢を変えた時に当たる確率は2倍。
そうそれ!1番分かりやすくて簡潔な解答だ
男『ここにABCD4枚のカードがあります。』
男『4枚のうち1枚が当たりです。』
男『私はどれが当たりか知っています。』
男『さあ、好きなの1枚選んで。』
女『じゃあA』
男『では、貴方の選ばなかったBCDのうちDはハズレであることを教えよう。』
(Dをめくる。確かにハズレだった。)
男『もう一度残ったABCの3枚から選び直していいよ。変えてみる?』
女『(モンティホールの応用だから変えたほうが若干得そうね)じゃあB。』
男『選ばなかったACのうちCもハズレなことを教えよう。』
(Cをめくる。確かにハズレだった。)
男『ラストチャンス。ABどっち?』
女『…(やっぱりAに戻したくなってきたw)』
女はAに変えるべきだろうか?
まず女が初めにAを選んだ時点でAが当たりの確率は1/4。
男がDがハズレであることを示してもAが当たりの確率は変わらず1/4なので、BC何れかが当たりの確率は3/4。このことからBが当たりの確率は3/8、Cが当たりの確率も3/8。AからBへ変更したことで当たりを引く確率が1.5倍になった為、女の直感は正しかったと言える。
ここで男が更にCもハズレであることを示した。女が選んだBが当たりの確率は3/8でAかCが当たりの確率は1/4+3/8=5/8。男による開示は確率に影響しないのでAが当たりの確率が5/8となり女はAに変えるべきである。
ただ、この考え方だと、男がDを開示したタイミングで女がAからBへ変更しなかった場合、Cを開示された後の確率はAが1/4でBが3/4になるんだよなー。女の選択次第でAの確率が変わるというのは違和感があるけど、そもそもAがハズレである確率が高い中、AとCの2択で男がCを開示した(Cがハズレだった)時点でAが当たりの確率が5/8になるのは妥当とも思えるし……。勿論、AとCが共にハズレで男が故意にCを開示したとなると話は変わってきますが。
どうでしょうか?
>男による開示は確率に影響しない
反例
当(A,B,C)=(1/2、1/2、0)
(選A、開B)
× 当(A,C)=(1/2、1/2)
○ 当(A,C)=(1、0)
確率0%は選択肢として成立しません。それはただの2択です。BがハズレであればAが必ず当たりになるのは2択だから当然です。これは反例にはなりません。
女が選んだもの(仮にAとする)が当たりである確率が1/3だとすると女が選ばなかったもの(仮にB及びCとする)のいずれかが当たりである確率は1-1/3=2/3になる。Bが開示された時、Bが持っていた当たりの確率がAやCに移るわけではなく、そもそも「Aが当たりの確率」と「BかCのいずれかが当たりの確率」という分け方をして考えているので男の開示が確率に影響しないと言っているのです。
>男の開示が確率に影響しない
そういう意味で言っているのなら、正しいと言えなくもないが
それを根拠にAが5/8になるという意味で言っているのなら、間違い。
ただの条件付き確率の問題で、正解は4/7。
当(A,B,C)=(1/100、1/100、98/100)
Aを選んでBが開示されたら、当たりはCでほとんど決まりなのは間違いないとしても、
Aを選んでCが開示されたら、当たりはBでほとんど決まり、
とまでは言いきれないことが直感でも分かるはず。
開示確率不影響説は、ある意味では正しいとも言えるが
ある意味では、選んでないBとCに対称性がある場合にしか成立しない。
当(A,B,C)=(1/3、199/300、1/300) なら以下略。
この問いを求めるpythonのソースコードをくだぱい。
宜しくお願い致します。
男『もう一度残ったABCの3枚から選び直していいよ。変えてみる?』
↑この時点でモンティホールのふりだしと同じ条件と考える。男は『A,B,Cのどれかに当たりが入っています。一枚選んでください』と言っているのと同じこと。
女が選んだBか男が持っているA,Cかのどちらを選択するかだけの話なので、Bのままなら1/3、Aに変えれば2/3が当たり。よってAに変えたほうが当たる確率は2倍になる。
男『もう一度残ったABCの3枚から選び直していいよ。変えてみる?』
↑この時点でモンティホールのふりだしと同じ条件と考える。男は『A,B,Cのどれかに当たりが入っています。一枚選んでください』と言っているのと同じこと。
女が選んだBか男が持っているA,Cかのどちらを選択するかだけの話なので、Bのままなら1/3、Aに変えれば2/3が当たり。よってAに変えたほうが当たる確率は2倍になる。
追記です。違った視点からの考察。
女がBを選んだ後に男がCをめくる可能性について。Cが当たりの確率が3/8なので、ハズレの確率は5/8。そのうちハズレがBCの場合の確率は2/8でこの場合はCをめくるしかない。ハズレがACの場合の確率は3/8でAとCのどちらをめくるのかが平等に選択された場合、Cをめくる確率は3/16。このことから男がCをめくる確率の合計は7/16。ハズレにCが含まれていた場合に故意にCをめくったとすると確率は5/8ですが、無作為に選択したと考えると、そもそもCがめくられる確率が7/16でAがめくられる確率が9/16。低確率であるCがめくられた時点でAの期待値は上昇する。のかな?と、思いました。
7/16(開C)=2/8(外BC)+3/16(外AC)
7(開C)=4(当A)+3(当B)
P(当A|開C)=4/7
P(当B|開C)=3/7
補足 (選A、開D)
P(A):P(B):P(C)=(1/4)*(1/3):(1/4)*(1/2):(1/4)*(1/2)=2:3:3
①当(A,B,C,D)=(1:1:1:1)
↓(選A、開D)
②当(A,B,C)=(2:3:3)
↓(選B、開C)
③当(A,B)=(4:3)
P(A):P(B)=(1/4)*(1):(3/8)*(1/2)=4:3
P(A)=4/7
P(B)=3/7
女はAに変えるべき
標準問題 (選A、開C)
P(A):P(B)=(1/3)*(1/2):(1/3)*(1)=1:2
P(A)=1/3
P(B)=2/3
極端な例 (選B、開A)
当(A,B,C)=9900/10000、99/10000、1/10000)
P(B):P(C)=(99/10000)*(1/2):(1/10000)*(1)=99:2
P(B)=99/101
P(C)=2/101
こうゆうのって理系が理系らしく説明しちゃうから
ますますわかんなくなるんだよね
これは負けパターンを考えると直感的にわかんじゃね
1-4の条件を経て負けるには当たりから変えてハズレしかない
ハズレから変えてハズレが無い
最初の3つのうち1つしかない当たりを引かないと
負けることが出来ない
だから2/3と言わざるをえない
モンティホール問題って、実は純粋な確率問題じゃないのかも。
他のコメントにも同じような考え方はありますが、要は、回答者が最初に当りのドアを選ぶか外れのドアを選ぶか場合分けして考えればよいだけかと。
つまり、
①回答者が最初に当りを選んだ時は、選んだドアを替えれば当然外れになります。
②逆に、回答者が最初に外れを選んだ時、司会者(モンティホール)は外れを開けるので、残るドアは必ず当っている訳で、選択したドアを替えれば必ず当る。
3つのドアのうち当りは1つだけなので、最初に選ぶ可能性(確率というよりは可能性といった方がしっくりくる)が高いのは外れの方。よって、②の場合になるので、変えた方が良いよってだけの話なんじゃないかと。
最初から1/3だの1/2だのと考えるからややこしくなるのでは。
このコメントに同意。ハズレを引ければ当たりだから確率は2/3。数学者でもなんでもありませんが。
そうそれ!
その考え方が一番分かりやすいわ
ハズレを選んでいた場合が当たりになるなら確かに2/3だね
そうそれ!
理系が大の苦手で確率という言葉や分数などが出てくるだけで拒否感が脳内を駆け回る人間ですが、これが一番わかりやすいです。
ものすごくざっくり言うと、「最初に選んだ時にはハズレを選んでいる可能性の方が高い。だから変えた方が良い」ということですね。ざっくり言い過ぎかな?
ひとつ上の回答者の匿名さんも「理系が理系らしく説明しちゃうからますますわかんなくなるんだよね」と言われていますがその通りです。
理系の問題を確率だとか1/3だとか理系っぽく説明するから理系が苦手な人は余計にわからなくなるのです。
1/3だとか小学生レベルの”数式”が出てきた時点で脳の半分は思考停止しますw 情けないことですが……。
みやねーさんの回答には数式も出てこないし、確率という言葉も「可能性」という言葉に置き換えてくれています。数学ではなく”国語的”なんです。さらには国語的にした文章も実に簡潔。
理系の問題をみやねーさんのように国語的になおかつ簡潔に説明してくれれば理解できるんです。少なくとも理解し易くなります。
「実は純粋な確率問題じゃないのかも」という一言もかなり救いになってくれています。「え?確率問題ではない?ということは数学ではないということ?だったら理解できるかも」と。
難しい数学を全て国語的にそして簡潔に”翻訳”してくれれば理系が苦手な人でも理解し易くなるかもしれませんね。
とか言ってる私が簡潔ではない長文になってしまいました。すみません。
つべに上がっていたマイクラで検証する動画のほうがわかりやすいですね。
この記事は教え方が回りくどいような気がしないでもない。
この問題は
出題者が必ず回答者が一つ最初に扉を選んだ後にハズレの扉を教えるという前提があってそこの部分が薄っぺらーく書いてあるから迷ってしまうだけで、この前提が崩れると出題者は相手の解答を誘導できてしまうのでね
まさにその通り。
1回選んだあとで、予期せず唐突に「変えてもいいですよ。」と言われたら、それは「司会者は自分を当てさせたいのか外れさせたいのか」を読む問題ですね。
肝は「再度選び直す」じゃなくて「必ず変更する」と考えることやね
そこが引っ掛かってました。
検討して変えない、
検討して変える、
はどういう扱いなのかと。
検討するしないではなく必ず変える、
だと納得です。
ベイズの定理を用いるまでもなく簡単にわかります。
第一に、回答者が正解の確率は1/3であり、この場合、つまり回答者が正解の扉を選択した場合、別の扉をあけたら100%の確率で失敗。逆に成功確率は0%
第二に、回答者が間違う確率は2/3であり、このばあい、つまり回答者が偽の扉を選んだ時に、変更したら100%の確率で成功。なぜならば、出題者は残り二つのどちらかの偽から一つを見せたので、別の扉は必ず正解ですから。出題者は偽の選択をしたのか否かを知っているのです。
回答者が成功する確率はこうなります
1/3×0 + 2/3×1 = 2/3。つまり変更しての正答確率は3/2。
(逆に変更しない場合は成功確率が 1/3となることも簡単にわかる。1/3×1+2/3×0=1/3
すなわち、変更しての成功確率は二倍。
計算すると実に単純ですが、鍵は何か?
出題者は正解を知っているので、回答者が正しい選択をした場合に、決してその正しい扉をあけないことにあるのです。この単純な事実こそ重要であり、ベイズの定理の本質を表現していると思います。
そうそれ!
司会者がハズレを必ず空けるので最初から1つは最初から無いと考えたら確立は1/2となる。
そして気が付いているだろうか?
並びが同じABCくじで、ハズレを必ず司会者が引くくじに対して3回引いてるから2倍になってるだけw。
1回しか引けないなら確立は1/2だよ。
司会者がハズレを必ず空けるので最初から1つは最初から無いと考えたら確立は1/2となる。
そして気が付いているだろうか?
並びが同じABCくじで、ハズレを必ず司会者が引くくじに対して3回引いてるから2倍になってるだけw。
1回しか引けないなら確立は1/2だよ。
そうそれ!
司会者が3つのうち必ず不正解を1つ開けるので確立は1/2になる。
この問題の場合はカードの位置が同じで3回引いたら2/3だけど、実際はワンチャンス!
この話はあくまでも並びが変わらず3回引いた場合の話w
1回しか引けないなら確立は変えても、変えなくても1/2
そうそれ!
司会者が3つのうち必ず不正解を1つ開けるので確立は1/2になる。
この問題の場合はカードの位置が同じで3回引いたら2/3だけど、実際はワンチャンス!
この話はあくまでも並びが変わらず3回引いた場合の話w
1回しか引けないなら確立は変えても、変えなくても1/2
この話はあくまでも並びが変わらず3回引いた場合の話ではなく、統計学的な確率においてです。
試行が少ない場合(ワンチャンス)は、確率通りにはなりません。
解説②が全然納得できん。
この説明だと100%当たらない?
私も解説2は理解できない。おそらく、解説が間違っている……
逆でしょ、解説2のパターンだと、100パーセント当たるよ。なぜなら、出題者はハズレしか開示出来ないからだ。なので、出題者が開示するドア以外を両方開けれるならば、100パーセント当たる。当選確率2倍所ではない。当選確率無限大。
なので、まぁ、解説2は間違っているので、混乱するのは記事を書いた人のせい、あなたのせいではない。解説2が間違っている。
え〜、おかしくね……?
解説1で直感的に理解出来たのに、解説2で余計分からなくなった。解説2って間違ってませんか……?おかしいと思うんだけど……
モンティ・ホール問題は理解出来たし納得出来たんだけど、解説2だけが理解出来ない……。
モンティ氏が開けて変えるって事は、最初に選んだ後に変えるのは、モンティ氏が開けたドアと、自分が変えた後のドアの2つのドアを開けるって事ですよね?モンティ氏が開けないドアを2つ開けるってのは、どう考えてもおかしいと思うんですが……
(´-ω-)ウム、どう考えても、解説2はおかしいです。変える事によって2倍になるのは、コメントしてる他の人が言っているように、出題者の手持ちカード2枚の方に賭けるからです。つまり、変えると言う事は、自分の手札と出題者の手札の交換。最初、出題者が2枚、回答者が1枚の手札なので、出題者の手札と交換すると、当選確率が2倍になります。解説2は、1枚が自分の手札でもう1枚が出題者の手札なので、当選確率は最大で2分の1にしかならない。ヘタすると3分の1のまま。自分の選んだ手札と出題者の手札を混ぜるな
この記事書いた人、全く分かってないんじゃないのか……?
コメント書いてる一般人の方が的確です……
逆でしょ、解説2のパターンだと、100パーセント当たるよ。なぜなら、出題者はハズレしか開示出来ないからだ。なので、出題者が開示するドア以外を両方開けれるならば、100パーセント当たる。当選確率2倍所ではない。当選確率無限大。
なので、まぁ、解説2は間違っているので、混乱するのは記事を書いた人のせい、あなたのせいではない。解説2が間違っている。
解説2は、挑戦者がドアを変更するとき、司会者と一緒にドアを開けても同じだと言っているのです。
最初に選んだドアがハズレなら、司会者はハズレしか開けられないので、この場合、100%挑戦者がアタリですが、最初に選んだドアがアタリの確率が1/3なので、ドアを変更した方が2倍確率が上昇します。
変える方法は、最初に当ててさえいなければ当たる。つまり1/3の当たりを引けてなければ当たるということ。なので2/3当たる。
逆に変えない方法は、最初からそのままなので、1/3を当ててればあたるということ。
ただ、変えた方が有利だけど、この位の確率なら最初に選んだ自分を信じたくなるかな笑
突然失礼します
モンティ・ホール問題を解いたのですが、別解を探していてこのサイトに辿り着きました。
Wiki等も参照したのですが、私の書いた解答 https://twitter.com/sesuda_kyonta/status/1177920520408354816?s=19 が手前味噌ではありますが一番(直感的に)分かりやすいように感じられました。
参照し、納得もしくは数学的に間違っている部分がありましたらご教示いただけますと幸いです。
また、コメント欄は余り目を通していませんので、もし先駆者の方がいましたら申し訳ありません。
第二チャンスを与えるとき、「最初にどれを選んでも第二チャンスを与える予定だった」という所まで伝えたのかな
伝えてない(or第二チャンスを与えない可能性もありえた)なら問題の前提が揺らぐけど……
変更しない場合は最初の選択の際に1/3の当たりを選ばなければハズレで、変更する場合は最初の選択の際に2/3の外れを選べば当たりだからって事だよな、これ
もしよろしければ、私の考え方を検討してください。よろしくお願いします。
正しいかわかりませんが、こう考えるのが一番スッキリすると思っています。
① 必ず変えると決めていたとき 当たる確率は 2/3
② 絶対変えないと決めていたとき 当たる確率は 1/3
③ 変える・変えないを決めていなかったとき 当たる確率は 1/2
③については、最後の選択の場面で当たる確率を1/2として計算しています。
このことから、「勝負事は、勝負する前から始まっている!」と思いました(笑)
解説2ですが、はじめにAを選んでいたとして、ホール氏がCのドアを開けると同時にAとBを開けるということでしたら、実質始めから2枚選んで1枚残るという選び方をしているから、モンティ・ホール問題とは別の問題のことになると思います。
ホール氏がCを開けてから、残った2つのAかBか、のうち、一つしか開けられないのですから。
テレビで見て全く持って理解できんかったが、このサイトを見てもやはり理解できんかった。
ハズレのドアが明かされた時点で分母が変わる、二択になるから、そうはならんやろとしか思えないです。
複雑に考えすぎやろ
疲れるでホンマ
解説①がとてもわかりやすかったです。
納得!
ありがとうございました。
納得できない
ホール氏が引いたハズレを除外すれば
ただの2択
1/2
なぜハズレだとわかっている選択肢を加味して確率に組み込まなければいけないんだよ
「アタリを引いていて変更したらハズレ」
「ハズレを引いていて変更したらアタリ」
なんだから2択でしょ
分母が間違ってる
モンテイホール問題の解答が納得できないのは
問題の解釈を間違っているからです。
この問題は「条件付き確率」を求めるものでは
ないので、司会者が「ハズレ」のドアを開けた時点での、確率を考えるのは間違いです。
モンティホールの問題で例として出される100(もしくはそれ以上)個の扉って
なぜか最初の問題であるはずれの扉のうち1つを開けるって部分を無視してるよね
はずれの扉を一つしか開けない原文ママだと1/100が1/98になるだけだから結局誤差だろって
なると思うんだけど
モンティホールの問題の解説として出される100(もしくはそれ以上)個の扉では
元の問題では最後に残った1個の扉が当たる確率と最初に選択した扉が当たる確率を比較しています。
したがって、はずれの扉98個を開けたときで説明しているのであって、はすれの扉を一つしか開けないときのことではありません。
論理で説明すれば全員が理解できるわけではないので、そういう方は以下のURLにあるExcelファイルで確認してみるのはいかがでしょう?
https://joho-ka.mints.ne.jp/monty-hall-problem-in-excel?doing_wp_cron=1581640846.4151310920715332031250
‘ VBA マクロ です。
Sub mh()
試行回数 = 1000
成功回数そのまま時 = 0
成功回数変更した時 = 0
For i = 1 To 試行回数
正解 = 乱数012()
視聴者 = 乱数012()
If 視聴者 = 正解 Then
Do
司会 = 乱数012()
Loop While 司会 = 正解 Or 司会 = 視聴者
Else
Do
司会 = 乱数012()
Loop While 司会 = 正解 Or 司会 = 視聴者
End If
If 視聴者 = 正解 Then
成功回数そのまま時 = 成功回数そのまま時 + 1
End If
Do
変更 = 乱数012()
Loop While 変更 = 司会 Or 変更 = 視聴者
If 変更 = 正解 Then
成功回数変更した時 = 成功回数変更した時 + 1
End If
Next
MsgBox “そのまま時: ” & 成功回数そのまま時 & vbCrLf & “変更した時: ” & 成功回数変更した時
End Sub
Function 乱数012() As Integer
乱数012 = Int(Rnd() * 3)
End Function
問題を変えます。3つの扉から2つ選んでください。選んだ2つから外れの扉を開けます。この時、扉を変えるチャンスをあたえます。あなたは、扉を変えますか。
それはただ三つ選んでるだけでは。(3/3開けられるのに開けない人はいない)
司会者の選ぶ扉が2つあって、片方を潰すので残った扉が2倍の重みになるという話が崩れる。
もし最後に開けられる扉が1つであれば、自分が2つ選ぶ価値が演出以外になさそうに見える。
というより変えないほうがいい確率が2/3になるだけ。
問題は変わっていないのでは。
匿名さん、返信ありがとうございました。もう誰からも返信がないと思っていました。その通り変えない方がよい確率が 2/3になると思います。選ばなかった扉に変えて開けてしまったら、数学的には損しそうですね。
では問題をもとに戻しましょう。3つの扉から、あなたが1つ選びます。残った2つの扉から、正解を知らない司会者が1つの扉を削除します。 (しかし、削除した扉は開けません)この時、開ける扉を変えるチャンスをあたえます。あなたは扉を変えますか?
1番最初の2018、9、25の匿名さんに先日、返信しました。いつまでたっても、文章が出てこなかったので不思議でしたが、日付の青い部分をクリックすると、いくつか後の返信にでていました。そういう仕組みになっているんですね。
この問題は私も初めは、 1/2だと確信していました。すごく不思議ですよね。杉並区のn中学のy先生の授業の中でこの問題が紹介されて、答えを聞いてそんなバカなと思いました。モンティーホール問題が、講談社文庫の「浜村渚の計算ノート」青柳碧人著に、出ていました。説明がややっこしかたですが、他にもおもしろい数学的なことが出てくるので、ぜひ読んでみて下さい。幾つかの図書館には置いてありました。今がチャンスかもしれまでんね。
私も9月25日の匿名さんの考え方は分かり易いと思いますが、
<出題者が手元の2つのうちの「ハズレ」を1つ開示しても、出題者の元に「当たり」がある確率は変わらない。ゆえに、出題者の手元に残っている開けていない方の扉が「当たり」の確率は2/3である。>
という説明は不適切だと思います。扉が「当たる」確率1/3が、「ハズレ扉」が分かったことで2/3になると誤解される危険があります。もし、この問題が、<「ハズレ」を1つ開示したとき、開いていない扉(最初の扉と残った扉)に「当たり」がでる確率(条件付確率)なら、答えは 1/2になります。
この問題は、1つの扉が「当たる」確率と、2つの扉が「当たる」確率を比較しているのです。
これは扉の数は、ぜんぜん関係ない。だますために扉が3枚とか言ってるだけ。
考え方としては、
無限大の数の扉から最初に1枚選択させる。
次に司会者が1枚提示する。
この2枚のうち、どちらかが当たりってだけ。
だから確立は2分の1
これって、3枚発行、1枚当たりの宝くじで、1枚と2枚とどっちが当たる確率が高いですか?っていう問いじゃないんですか。私が1枚、あなたが2枚持っているとします。当たりの確率は私が1/3、あなたが2/3です。で、あなたはハズレを1枚私に見せます。が、その行為自体には意味はありません。なぜならあなたは必ず1枚はハズレを持っているからです。ただ単に1枚と2枚(の権利といったほうがいいかもしれません)を交換するかしないか、という選択を突き付けられている、と考えれば一番シンプルだと思います。開示自体がミスリードのためのギミックなのではないでしょうか。
☆ホールが無作為である時の場合分け
① a(当たり)をモンティが選ぶ
この時、場合はb(ハズレ)を選ぶホールとc(ハズレ)を選ぶホールに分けられます
※「ハズレ」という点では同じだが、場合分けにおいてはこの時点で2通りある
② a(ハズレ)をモンティが選ぶ
b(当たり)のとき、c(ハズレ)をホールが選ぶ
c(当たり)のとき、b(ハズレ)をホールが選ぶ
b(当たり)のとき、b(当たり)をホールが選ぶ
c(当たり)のとき、c(当たり)をホールが選ぶ
これが純粋な『ホールが無作為である場合』の場合分け
ご覧の通り、ホールは当たりを引きかねないので場合の合計は6通りになりますね
この内、モンティが扉を変えずに「当たり」を得る場合は合計で2通りあります
☆ホールが作為的にハズレを選ぶ時の場合分け
①に関しては先ほどと変わらず2通り
②a(ハズレ)をモンティが選ぶ
b(当たり)のとき、c(ハズレ)をホールが選ぶ
c(当たり)のとき、b(ハズレ)をホールが選ぶ
①と②を合計して4通りしかありません
つまりホールは無作為なら選ぶかもしれなかった2通りの場合(当たりを引く場合)を作為的に消してしまったことになります
よって、6/6−2/6=4/6より2/3となるのです
☆よくある勘違いの例(場合分けをしない)
①a(当たり)をモンティが選ぶ
b=c(ハズレ)をホールが選ぶ……区別すべき2通りのハズレを同一視してしまう
②a(ハズレ)をモンティが選ぶ
b(ハズレ)をホールが選ぶ
c(ハズレ)をホールが選ぶ……当たりの時のみ区別してしまう
モンティが扉を変えずに当たりを選ぶ確率は1/3だから変えた時の確率が2/3! という解法に至る
モンティが外れの扉を選ぶのは、「残った2枚の扉」からです。この時は、扉を変えて当たる確率は、3分の2。
では、機械が3枚の扉から、無作為に外れの扉を選んだらどうでしょう。当然回答者の選んだ扉が外れの場合、その扉が選ばれることがあり、この時は絶対変えなくては当たりませんね。それでは、機械が「3枚の扉から無作為に外れのどちらか1枚選んで開ける」時に、選んだ扉を変えた時に当たる確率はどうなりますか。
IQはそもそも何を見ているのかというと、実は、物事の共通性を瞬時に見抜く力
なんですよね。だから、世界一のIQの彼女には、この手の問題が一番得意なんだよね。私もしかるべき機関でIQをはかり、彼女には負けますが(200超えはすごい)、極めて高いIQでした。
解説の1つ目は上手ですよね。みなさんの書き込みの中江では、一番IQの高い説明は、goodluckより: 2020年2月9日 8:50 午前 です。
ちなみに高IQと博士号はもちろん、ノーベル賞さえも関係ありません。
高IQは一種の超能力です。
確率と組み合わせを一緒にしないでください。
確立の理論というのはモンティーホール問題でほぼ説明がつきます。
モンティーホール問題の説明を軽くしておくとこうです。
ロスアラモス国立研究所の実験でわかったことで、扉を変えるならば約66.7%、すなわち2分の3の確率で景品があたる。ということなのです。
これを説明しておけば複雑な文章でなくても理解いただけけるのではないのでしょうか。
つまり、何かを変えるというのは、ある場面においてはいいことかもしれません。
なるほど。変えると確率は上がるということですね
!
これは結局、最初に選んだ一枚か、残った二枚か、どちらを選ぶのってだけの話なんよね
モンティ氏はただ作為的に、選ばなかった方に必ずあるハズレの扉を開けているだけにすぎない
一枚と二枚の勝負なので、試行回数を重ねれば必ず二倍の勝率差に収束していく
扉を変えても変えなくても正解の確率は同じ。
司会者がはずれの扉を開けたときに、扉を変えないを選んだ時の正解の確率が2/3に上がります。
変えない時だけ確率が変わらないというのが錯覚です。
説明もとても分かりやすかったのですが、B’zのTreasure特典のトランプを使用していることに興奮しました!!笑
最初に挑戦者が選ぶという行為は、正解する確率に全く影響しない。挑戦者が朝、歯を磨いたかどうかが影響しないのと同じ無関係なイベント。
司会者が選択枝を2つに減らしてから、2つの中からどちらかを選択した場合の正解の確率でしかない。
つまりこの問題の答えは、変える場合も変えない場合も1/2の確率で正解する。
それは違う。
3枚中1枚当たりの宝くじがあり、変えないのが1枚貰えた状況、変えるのが2枚貰って主催者がその一枚のはずれを教えてくれ破り捨ててくれた状況と同等だから。1/3と2/3なら当然変える。
私はこう現実的に想像してようやく納得しました。
最初にはずれを引いて途中で変えた場合、当たるので、当たる確率は2/3。なので、途中で変えると当たる確率が倍になる。
ホルトとケビンの口論
ヤバイ
コメント多杉田玄白
今日で犬養毅死んで89年やなー
私は頭が悪いので良く分からないのですが、私にはこう思えました。
①最初の3枚の中から1枚のドアを選んで、モンティーホールがハズレを必ず開ける(回答者が当たっていようが外れていようが)
②そのあとに決まり文句の『変えますか?』と聞くなら
元々2枚のドアで当たりを決める(元々の回答が意味のないものと考えて)、という事になり、初めから2分の1だった、という事にはならないのでしょうか?
最初が3分の1だった、と考えるのは違う様な気がしました。
最初の選択が無意味なのでは?ないかと思いました。
意味わからん?
当たりを選べと分母を削るなら1/2でしょう。
1/3から外れを1枚選んでいく、その際に再度質問して選びなおすんだから、
次は分母が1減って1/2でしょう?
仮に選択肢の中に司会者が選んだ外れも選べるのなら話しは別ですが、最後は
50%以上にならないのではないですか?
⁉︎匿名さん死刑囚のパラドクスを知らない!?
この問題の条件下に限ってめっちゃ単純に言えば、
ヤギを引く確率(ヤギの数と言ってもいい)がそのまま正解の確率なのだ。
つまり、必ず変えるという信念の下であれば、どちらのヤギを選んでも正解に至る(2/3)。
その信念の下、唯一車を引いた場合はハズレに至る(1/3)。
ってことは、確率は2/3だとわかるね。
司会者がハズレを引かなかったり、変更しなかったり、ヤギの数が増えたり、所与の条件が変わると違う結果になる。
犬養毅のコメントに対して誰か反応してくry
はじめまして、ほんだなばいくと申します。
非常にわかりやすく解説されており、参考記事としてブログへ転載させて頂いてもよろしいでしょうか。
結局、人が関わっている時点で確率はどうとでもなるわけで…
3個でも100個の扉でも同じ。
確率というか…言ってしまえば運の問題。
この運ってのは人によって全く違うと思っています。
何回やってもハズレを引く人もいれば、
何回やってもアタリを引く人もいる。
世界各国、もしくは日本、その地域で、
運がある人、全くない人の選別も可能かもしれないですね。
運の無い人はこれに限らず全体的に運が低いでしょうし。
そんな私もその1人です。
ダイスを使うゲームは色々ありますが、
ことごとく他の人よりもダイス目が悪く、何をやってもどんな種類のものをやっても目が悪い。
高い数値が良いゲームでは低いのが多く出て、
低い目が良いゲームでは高い目がよく出る。
ゲーム以外でも日常的なことでも運が悪いことが多い。
環境や確率、色々なものが影響しますが、
人が関わるとその人の意識行動が関わってくるので、
運、確率なんていくらでも変動するということですね。
なので神も仏もありません。
変えたほうが2倍とかの計算は分からないけど変えたほうがいいのは分かりそうなもんだがな。
普通に考えたらまず外れを選ぶ可能性が高い、で司会者が外れをとっぱらう、で変えれば一番当たりそうなのに数学者はどういう考えしてるんだろうな。
1990 年にマリリンちゃんが雑誌に解説した問題を30年後の現在まだ議論したはりますね。
この問題は「3囚人問題」とか「死刑囚のパラドックス」とかいわれる昔からある問題と同型ですが、議論すべきなのは「ことば」の問題なんです。
「モンティ・ホール問題」はわれわれが日常使っている言語(自然言語)で書かれています。数学の教科書も自然言語を使わなければ書けません。
そこでこういう問題が起きます。
「ある問題が自然言語で表現された。この問題が数学的な問題(数学的にあいまいでない問題)といえるかどうかを判定するアルゴリズムは存在するか。」
これはもうとっても難しい問題です。「論理哲学」の問題と言ってもいいかな。
どうも納得できないな。
すべての事象を可視化してみたらこうなると思うけど、間違っているかな?
ABC のうちAが車。BCはヤギとして
① 最初選択がAで、司会者選択B、その後変更ならCでハズレ。
変更なしならAでアタリ。
② 最初選択がAで、司会者選択C、その後変更ならBでハズレ。
変更なしならAでアタリ。
③ 最初選択がBで、司会者選択Cのみ、その後変更ならAでアタリ。
変更なしならBでハズレ。
④ 最初選択がCで、司会者選択Bのみ、その後変更ならAでアタリ。
変更なしならCでハズレ。
これ以外の事象はないと思うけど
総じて、選択を変えるとハズレ2、アタリ2. 変えなければハズレ2、アタリ2
つまり変えても変えなくても確率は同じになる。
変わらないと思う。
そもそも司会者がハズレのドアを知っていて、開けた時点で最初の確率1/3は崩れるのでは?
上の事象可視化以外の可能性ってあるかな??
わー、すごいですね!!
回答者が最初に選んだドアが「当り」である確率は1/3です。しかし,司会者が「外れ」を開けた後では,最初に選んだドアが「当り」である確率は1/2に変わり,残りの一つのドアが「当り」である確率も1/3から1/2に変わります。これは言わゆる非復元抽出の例であり,選ぶドアを変えると「当り」である確率が2/3になるというのは単純な誤りです。
自分は昔から「家を出てくる時から、必ず変えると決めてゲームに参加する」。そして「最初に引く確率は当たりが3分の1で、はずれが3分の2である」ということ。必ず変えるということは必ず「当たりははずれに、はずれは当たりになる」ということ・・・。これらを組み立てたらトリビアリー!w
凄いよな、語り尽くされ完全な結論も出てて、親切丁寧な説明もあると言うのに。。ゲノム解析されてそうなのがこんだけ居るのは完全なホラー。
よくわかった。
よくわかった。
元々ハズレを引く可能性は3分の2だから変えたら当たる確率は2倍になる
という考え方は間違ってますか?
元々ハズレを引く可能性は3分の2だから変えて当たる確率も2倍になる
という考え方は間違ってますか?
ピンバック & トラックバック一覧
[…] https://analytics-notty.tech/very-good-explain-montyhall-problem/ […]
[…] […]