素数ゼミの謎 – なぜセミは素数を選んだのか

2018年1月22日2020年5月19日

素数とは？

素数について簡単におさらいをしておきましょう。※もう知っているという人はこの章は飛ばしてもらって構いません。

”素数”とは、1と自分自身でしか割れない数のことをいいます。ただし1は含まれません。

 

例えば、7などは素数です。1と7では割り切れるけど、その以外にこの数を割ることができないからです。

一方、8は素数ではありません。1と8で割り切れるほかに、2や4でも割ることができます。

20までの素数を挙げると、

$$2, 3, 5, 7, 11, 13, 17, 19$$

です。ここでは、素数の中でも”13″と”17″が活躍します。

 

スポンサーリンク

素数を好むセミ”素数ゼミ”

自然界には、自分たちの種を残すため、様々な進化を遂げる生き物たちがいます。

その中で、進化するために数学を利用する昆虫がいるのですが、それが”素数ゼミ”と呼ばれるセミです。

セミには、数年から十数年周期で大量発生する種類のものがいます。

これらのセミを周期（しゅうき）ゼミと呼びます。ある一定の周期で大量発生するからですね。

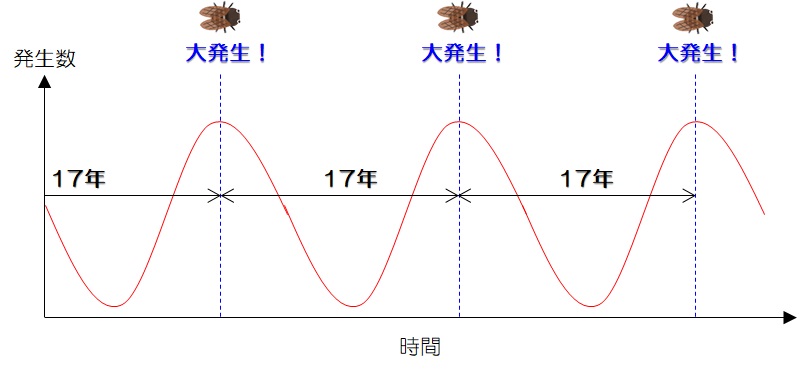
その中でも、周期が素数（13年や17年）であるセミを”素数ゼミ”と呼びます。

素数ゼミは主に北アメリカ東部に生息しており、その中でも17年周期のセミは北部、13年周期のセミは南部に生息していると言われています。

素数ゼミは、たまたま素数を周期としたわけではなく、種の存続を有利にするため（種として生き残るため）数学的な根拠があっての理由から素数を選ぶようになったのです。

ここでは、素数ゼミがなぜ素数を選ぶように進化していったのか、面白くて神秘的な理由を紹介しましょう。

 

セミが素数を選んだ理由（その１）

素数ゼミ以外にも多くの動物は、ある周期で大量に発生しています。

例えば、セミの天敵は鳥ですが、鳥は3年や4年周期で大量に発生します。

 

セミが大量発生した年に、たまたま天敵の鳥が大量発生してしまったらどうでしょう？

鳥は好物のセミが多く取れて繁殖できますが、一方セミは一網打尽です。下手すると絶滅してしまう可能性だってあります。

 

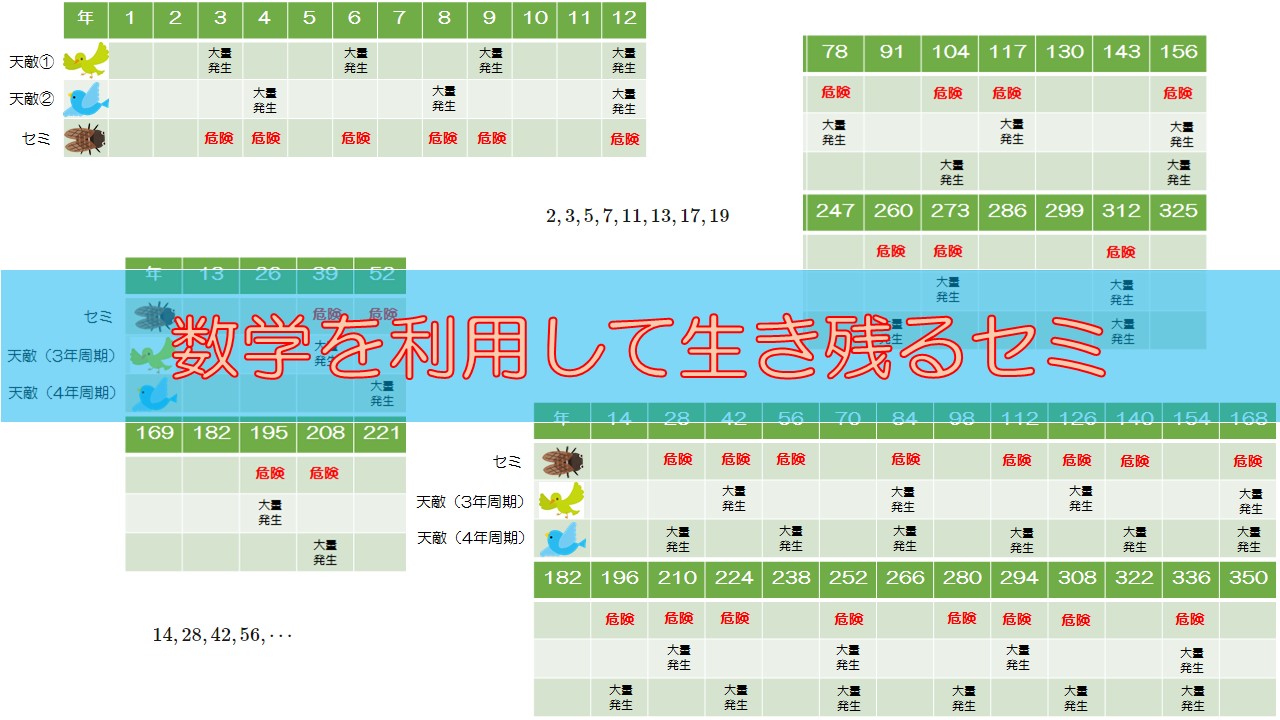
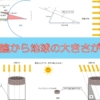
下の図はセミの天敵①が3年周期、天敵②が4年周期で大量発生する場合に、セミが大量発生してしまっては危険な年を表しています。

セミの天敵（主に鳥たち）が大量発生するときに、セミも大量発生していては危険ということです。

 

そこで、セミはできるだけ天敵と出会わないようになる周期を選ばないといけません。そして、セミの周期は12～18年ぐらいがちょうどよいという条件も考えなければいけません。

つまり、セミにとって最も良い周期の条件は、

1. 天敵の大量発生にできるだけ合わない
2. ただし、周期の長さは12～18年

という二つを満たすことになります。

そして、この二つの条件を満たす最も良い周期として、素数の13と17が選ばれたのです。

 

スポンサーリンク

確かめてみよう

では、本当に13と17の素数の周期が最も良い周期であるのかを確かめてみましょう。つまり、最も天敵と出会わない周期であるかを調べるということです。

まずは、素数ではなく14年周期の場合を考えます。14年周期でセミが大量発生するとして、3年周期の天敵①と4年周期の天敵②がいたとします。

セミが大量発生するのは、14の倍数の年なので、

$$14, 28, 42, 56, \cdots$$

です。これらの数字が3もしくは4の倍数のときに天敵も大量発生してしまいます。

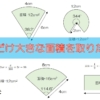
セミの大量発生が25回起こる場合に天敵たちの大量発生に合う場合を下の図に示しました。

セミが天敵の大量発生とかち合う回数は、16回です。

25回中16回ですから、64%の確率で危険ということになります。

 

では、同じように素数である13年周期の場合も考えてみましょう。セミの大量発生は同じく25回とします。

こちらは危険な回数は12回となり、確率は48%です。

初めにみた14年周期の場合に比べて、16%危険が減少しています。

 

同じように素数の17年周期を考えても確率は13年周期の場合と同じ48%になります。

このように、セミは自然の中で種を残すために一番合理的な”素数”を選んだのです。

 

セミが素数を選んだ理由（その２）

ここまでは、セミの天敵を避けるためには”素数”が一番合理的な周期であることを説明してきました。

しかし、素数を選ぶのは天敵を避けるためだけではありません。

素数はセミ同士でも交配（交尾）にも有効的に機能しているという説もあります。

静岡大学大学院の吉村仁教授の研究によると、同じ種の近隣種との交配はその種の絶滅リスクを上げると言われています。近隣種との交配は無い方がよいのです。

近隣種とは、似た種だけれど同じ種ではないものです。

 

例えば、13年周期のセミの近隣種に10年周期ゼミや15年周期ゼミがいたとします。13年ゼミはこれらのセミとできるだけ交配を行いたくありません。

なぜでしょうか？

例えば、13年周期のセミと16年周期のセミが交配して生まれてくる（雑種ともいえる）セミは、どのくらいの周期で大量発生するセミになっているでしょうか？

それは、13と16の間の14や15する可能性がありますよね。つまり、これまでとは違う周期のセミが誕生するわけです。※確実にそうなくるとは言い切れませんが、その可能性は高いと考えられます。

 

これでは、次にこれらのセミが大量発生するときは、周りのセミの数が減ってしまうことになります。

つまり、トータルのセミの数は変わらなくても、いろんな周期のセミができてしまうと、一度に発生する数がばらけて、同じ年に一緒に地上に出るセミは少なくなるということです。

これにより、セミはできるだけ同じ周期を持ったセミ同士で子孫を残したいのです。

 

そこで、素数が役に立ちます。

素数を使えば、天敵と出会う確率が低いことは既に説明しましたが、これは近隣種との出会いを考える上でも同様です。

素数の周期を持っていれば周期の違う近隣種と会う確率が低くなり、危険な交配の機会も少なくなるのです。

 

例えば、13年周期の素数ゼミと15年周期のセミが、同時に大量発生したのが2000年だとします。次にこれらが同時に大量発生するのはいつでしょうか？

まずは13年周期の素数ゼミの大量発生の年を並べてみました↓

【13年周期の素数ゼミ】
2000, 2013, 2026, 2039, 2052, 2065, 2078, 2091, 2104, 2117, 2130, 2143, 2156, 2169, 2182, 2195, …

ただ、2000年から+13づつ増やしていっただけですね。

次に、15年周期の素数ゼミの大量発生の年を同じようにして計算していきます。その途中で、上の上の年と同じ年が現れればその年が次に素数ゼミと出会う年です。では、書いてきましょう。

【15年周期の素数ゼミ】
2000, 2015, 2030, 2045, 2060, 2075, 2090, 2105, 2120, 2135, 2150, 2165, 2180, 2195!

2195年でようやく同じ数字が現れました。つまり、一度出会ったら次に出会うのは195年先ということです。これは長いですね。

では、15年周期のセミと18年周期のセミはどうでしょうか？これらは素数ゼミではありません。しかし、18年周期というのは先ほどの13年周期よりも長いですので、もっと出会う確率が低いような気がしませんか？

では、考えていきましょう。先ほど、15年周期の年は書いたので、18年周期を書いていき、どこで同じ数が現れるかをチェックしましょう。

【18年周期の素数ゼミ】
2000, 2018, 2036, 2054, 2072, 2090!

あれ？！90年後には同じになってしまいました。やっぱり、出会わないためには素数であることが必要ということですね。

 

ここで紹介した素数ゼミの他にも、自然には数学をうまく利用した生物、現象がたくさんあります。

自然は数学で溢れているのです。面白いですよね。

 

素数についての不思議に惹かれた人は、以下の記事も是非読んでみてください。

 

スポンサーリンク

まとめ

• 13年や17年周期で大量に発生するセミが存在する（素数ゼミ）
• 素数ゼミが素数を好んで使うのは、天敵である鳥の大量発生とできるだけ発生の年が重ならないようにするため
• もう一つの理由は、近隣種との危険な交配を避けるためでもある