【数学クイズ・パズル】死刑になる囚人が喜んだのは正しい？ – 囚人の確率問題

2018年3月11日2020年5月20日

死刑になる囚人が喜んだのは正しい？

確率の問題によく登場する三人の囚人の話の一つです。

人間の直観がいかに正しい判断を行えてないかを知らしめてくれる代表的な数学パラドックスです。

あなたはこの問題に対して正しい判断ができるでしょうか？

では、問題を紹介しましょう。

問題

 

あなたは、この囚人の「釈放の確率が\(1/3\)から\(1/2\)に上がったと」いう判断は正しいものだと思いますか？

 

この考えは一見正しそうに聞こえます。

釈放候補から囚人Bが消えたことにより、囚人Aか囚人Cが釈放です。

二人の囚人AとCは同じ確率で釈放なのですから、どちらかが選ばれる可能性は半々の\(1/2\)ではないのでしょうか。

 

ここで答えを言ってしまいますが、この判断は間違っています。

囚人Aが釈放になる確率は、\(1/3\)のままです。

なぜでしょうか？

 

解説

ちゃんとした証明には、”ベイズの定理”というものを使わなくてはいけませんが、ここでは他も方法で理解することを目的としましょう。

下の画像は復習です。囚人Aが看守に聞いて、囚人Bは釈放されないと言ったのでしたね。

看守が「囚人Bが釈放されない」という場合はどんな時があるでしょうか？

すべてのパターンについて考えてみましょう。

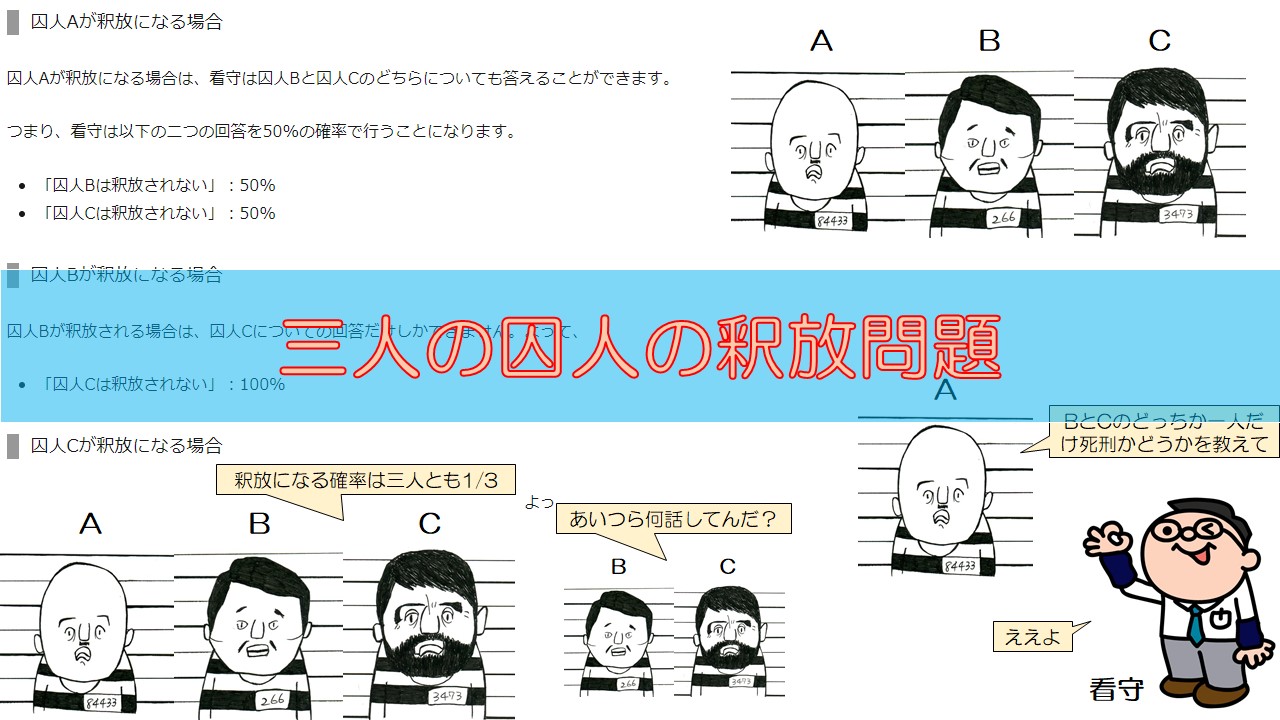
囚人Aが釈放になる場合

囚人Aが釈放になる場合は、看守は囚人Bと囚人Cのどちらについても答えることができます。

つまり、看守は以下の二つの回答を50%の確率で行うことになります。

• 「囚人Bは釈放されない」：50%
• 「囚人Cは釈放されない」：50%

囚人Bが釈放になる場合

囚人Bが釈放される場合は、囚人Cについての回答だけしかできません。よって、

• 「囚人Cは釈放されない」：100%

囚人Cが釈放になる場合

囚人Cが釈放される場合は、囚人Bについての回答だけしかできません。よって、

• 「囚人Bは釈放されない」：100%

です。

 

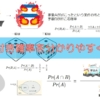
しかし、いま看守は「囚人Bは釈放されない」と回答しているので、可能性としては、以下の二つです。

• 囚人Aが釈放されるので「囚人Bは釈放されない」と言っている（50%）
• 囚人Cが釈放されるので「囚人Bは釈放されない」と言っている（100%）

ここで右端に示した確率に注目です。

 

どちらも看守の回答は「囚人Bは釈放されない」ですが、囚人Aが釈放される場合に言う確率と、囚人Cが釈放される場合に言う確率は違っているのです。

囚人Cが釈放される場合に「囚人Bは釈放されない」という確率を\(1\)とすれば、囚人Aが釈放される場合に言う確率は\(1/2\)です。

つまり、囚人Aが釈放される確率は、

$$\text{囚人Aが釈放される確率} = \frac{\frac{1}{2}}{1+\frac{1}{2}} = \frac{1}{3}$$

です。

囚人Aにとっては残念ですが、看守の回答を聞く前と後では、釈放になる確率は変わらなかったということですね。

 

スポンサーリンク

ベイズの定理

このような確率の問題を”条件付き確率”問題と言います。

この問題をちゃんと証明しようと思ったら、”ベイズの定理”というものを理解する必要があります。

以下の記事で分かりやすくベイズの定理を紹介していますので、是非学んでみてくださいね。

 

囚人が登場する数学クイズはこちら↓からどうぞ。

 

まとめ

• 三人の囚人の釈放確率に関する問題について紹介した
• 人間の感覚的な確率はあてにならない（数学パラドックス）
• ここで紹介したような問題をきちんと証明するには”ベイズの定理”を学ぶべし