ベルトランのパラドックス – いろいろな確率になる数学パラドックス
パラドックスとは、”一見正しいと思えるようなことが、詳しく知ってみると実際は思ってもみなかった結果になる”ということです。
確率に関する数学パラドックスは、多くあります。
それは、確率が人間の直感では理解しにくいものであるためです。
ここでは、そんな確率について考えさせられる”ベルトランのパラドックス”という問題を紹介しましょう。
ベルトランのパラドックスとは
有名な確率のパラドックスに”ベルトランのパラドックス”というものがあります。
ここでは円の中にランダムに線を引く方法を考えていくのですが、そんな単純な作業が人間の頭を混乱させてしまいます。
確率の意味を考えるのに適したパラドックスです。
では早速、”ベルトランのパラドックス”を説明していきましょう。
スポンサーリンクいろいろな確率になるベルトランのパラドックス
問題
まずは、問題を紹介しましょう。
問題は誰でも理解できるほど簡単です。
まず、円を描きます。
この円に内接する正三角形を描きます。
ここで問題です。
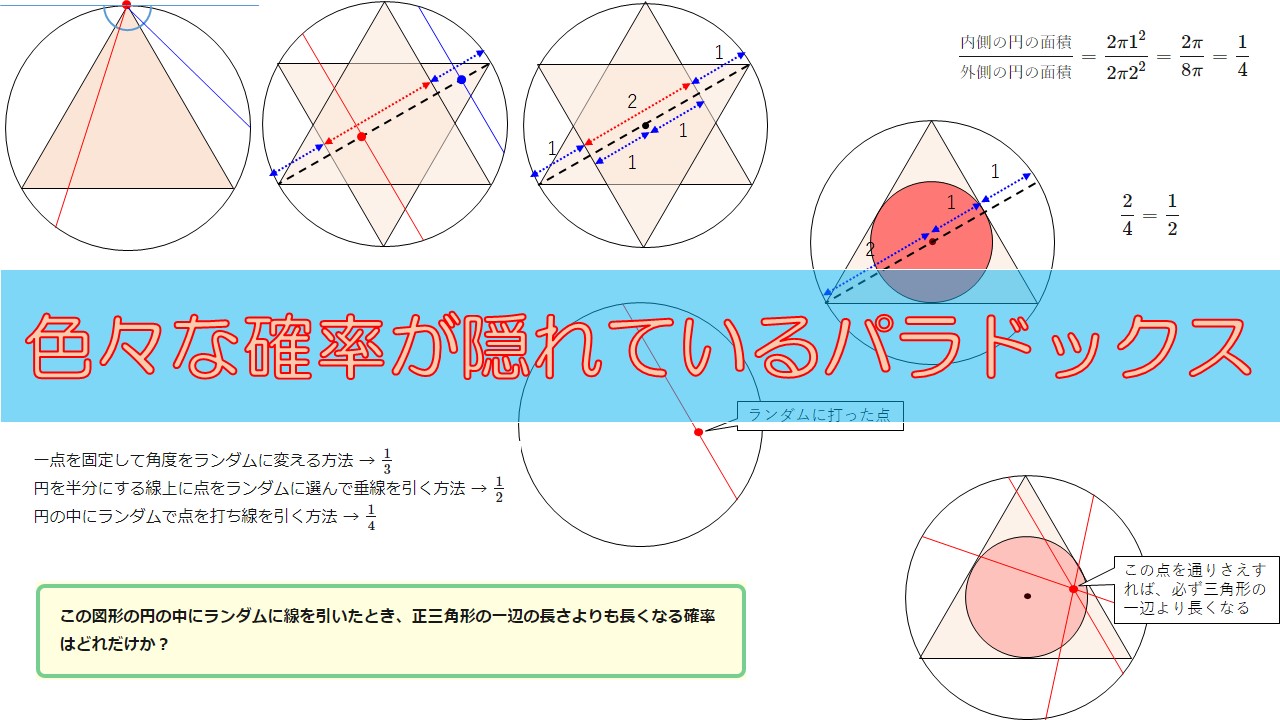
この図形の円の中にランダムに線を引いたとき、正三角形の一辺の長さよりも長くなる確率はどれだけか？
ということを考えましょう。
これが、”ベルトランのパラドックス”の問題部分です。
例えば、適当に以下のように線を引いてみました。
これは、三角形の一辺の長さと比較して長い線ですね。
では、次のような線はどうでしょう。
これは明らかに三角形の一辺よりも短い線となっています。
このように”ランダムに線を引いたとして、三角形の一辺よりも長い線となる確率はどのくらいでしょう”というのがベルトランパラドックスの問題です。
三つの異なる解答
そして、ここからがパラドックスを生じさせる部分に入っていきます。
上で説明したベルトランの問題に対して、以下のような三つの解答が用意されています。
（解答その①）一点を固定して角度をランダムに変える方法
ランダムな線の引き方を考えてみましょう。それは、以下のような方法が考えられます。
線を引くためのスタートとなる点を円周のどこかに決めます。
この点から直線を引きますが、円の内部にしか線を引けないので線を引っ張れる可能な角度は、下の図のように180度になります。
ここで、三角形の一辺の長さよりも引いた線の長さが長くなるのはどんなときでしょうか？
例えば、以下の図を見てください。
赤い線は三角形の辺の長さよりも長いですが、青い線は短いことが分かります。
これより、三角形の辺の長さよりも長くなる条件は、
引いた線が三角形の角度内（上の図のピンク色が付いた範囲）になるとき
であることが分かります。
正三角形の角度は60度です。
ランダムに線を引ける角度は180度ですが、そのうち60度内に入れば三角形の辺の長さよりも長くなります。
よって、ランダムに線を引いたとして、三角形の一辺よりも長い線となる確率は、
\begin{align}
\frac{60}{180} = \frac{1}{3}
\end{align}
となり、答えは\(1/3\)となることが分かります。
ここで行った操作は、円をどのように回しても成り立つものですので、どのような円周上の点を選んだとしても変わらない議論ができます。
どうでしょうか？何か腑に落ちないことはありましたか？
なければ、次の解答に進みましょう。あってもとりあえず次に進みましょう。
（解答その②）円を半分にする線上に点をランダムに選んで垂線を引く方法
次は、円を半分にする線上に点をランダムに選んで垂線を引く方法です。
まず、円を半分に切る直線（下の図の点線）を引きます。
この点線のどこかをランダムに選び点を付けます。
この点に垂線を引くように円内に直線を引きます。
このとき、赤い線は三角形の一辺の長さより長く、青い線は短いことが分かります。
では、どのようなときに三角形の一辺の長さより長くなるのでしょうか？
以下の図は、もう一つ正三角形を逆向きに重ねて描いた図です。
このとき、赤い両矢印（⇔）の範囲内に点が入れば、三角形の一辺の長さより長くなります。
一方、青い両矢印（⇔）の範囲内に点が入れば、三角形の一辺の長さより短くなります。
点の取り方はランダムですので、確率はそれぞれの範囲の長さと考えていいでしょう。
赤い両矢印（⇔）の範囲の長さを考えましょう。
ここでは、円の半径を\(2\)とします。
すると、正三角形の角の角度は\(60\)度であるので、以下のようになります。
よって、
となり、これで赤い範囲と青い範囲の長さが分かります（下の図）。
ランダムに選ぶ点が、円の直径が\(4\)のうち、赤い範囲の\(2\)に入れば三角形の一辺の長さより長くなりますので、その確率は、
$$\frac{2}{4}=\frac{1}{2}$$
です。
よって、三角形の一辺の長さより長くなる確率は、\(1/2\)となります。
あれっ！？
はじめに説明した方法（一点を固定して角度をランダムに変える方法）では、確率は\(1/3\)でしたが、今回は\(1/2\)です。
なぜでしょうか？
あまり深く考えずに最後の三つ目の解答へ進みましょう。
（解答その③）円の中にランダムで点を打ち線を引く方法
最後の方法は、円の中にランダムで点を打ち線を引く方法です。
例えば、以下のように円の中にランダムで点を打ちます。
この点から線を引くという方法です（下の図）。
このとき、三角形の一辺の長さより長くなる場合を考えてみましょう。
円の半径を\(2\)とすれば、一つ前の”円を半分にする線上に点をランダムに選んで垂線を引く方法”で見たとおり、
です。
ということは、下の図の赤い円の中に点があれば、三角形の一辺の長さより長くなることが分かります。
例えば、以下の図は赤い円内に点が打たれた場合の線の引き方ですが、どのように引いても三角形の一辺の長さより長くなります。
ということで、外側の円内にランダムで点を打ち、それが内側の赤い円の内側になる確率が、三角形の一辺の長さより長くなる確率なので、それぞれの円の面積を考えて、
$$\frac{\text{内側の円の面積}}{\text{外側の円の面積}} = \frac{\pi 1^2}{\pi 2^2} = \frac{2 \pi}{8 \pi} = \frac{1}{4}$$
となります。
よって、三角形の一辺の長さより長くなる確率は、\(1/4\)となりました。
またまた、前の二つの方法とは確率が変わってしまいました。
何がいけないのでしょうか？
ベルトランのパラドックスの考察
ここまでベルトランの問題に対して三つの解答を紹介してきました。
解答をまとめておきましょう。
- 一点を固定して角度をランダムに変える方法 → \(\frac{1}{3}\)
- 円を半分にする線上に点をランダムに選んで垂線を引く方法 → \(\frac{1}{2}\)
- 円の中にランダムで点を打ち線を引く方法 → \(\frac{1}{4}\)
というように、すべての答えが違っていました。
どの方法が正解で、どの方法が間違いなのでしょうか？
答えは、
どの方法も間違いではない
です。
すべての方法はどこにもおかしな点はありませんでした。なので、どの方法も間違っていないのです。
では、なぜすべての方法で違う確率になるのか？
それは、問題の”ランダム”という意味があいまいであったことが原因です。
ランダムといっても様々なランダムがあります。
どのようにランダムであるのかを明示しなければ、今回のように問題を解く人が勝手にランダムの定義を作るしかありません。
ランダムの定義が作る人によってバラバラであれば、今回のようにそれぞれ異なった解答が出てくるのです。
ベルトランのパラドックスとは、ランダムという意味の捕らえ方には様々なものがあり、きちんとランダムの定義を作ることが重要であることを教えてくれる問題
だったのです。
スポンサーリンク
まとめ
- ベルトランの問題は、円の中にランダムに線を引いたとき、内接した三角形の一辺の長さよりも長くなる確率を求める問題
- ここでは、三種類の解答を紹介したが、すべての解答で答えが異なっていた
- すべての解法は間違いではなく、問題を解く人が勝手にランダムの定義を作ったことによって生じたものである
- ベルトランのパラドックスとは、ランダムという意味の捕らえ方には様々なものがあり、きちんとランダムの定義を作ることが重要であることを教えてくれる問題