正方形を利用した三平方の定理の証明
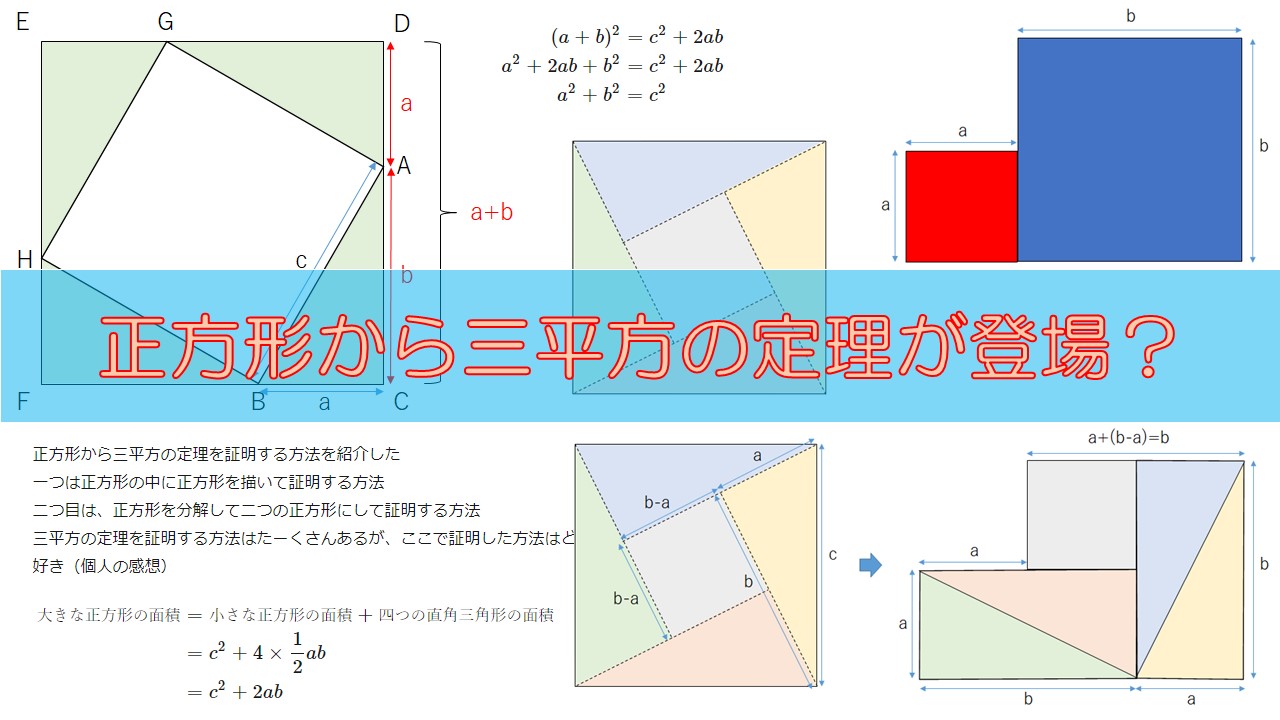
100種類以上あると言われている三平方の定理(ピタゴラスの定理)の証明方法ですが、その中から今回は、”正方形を使った三平方の定理の証明”を紹介します。
正方形の中に正方形を描いて証明する方法
まずは、正方形の中に正方形を描いて三平方の定理を証明する方法です。
まずは、大きな正方形を一つ描きましょう。

この中にもう一つ小さな正方形を描きます。以下のような図の感じです。
すると、大きな正方形の中に小さな正方形が一つと、直角三角形が四つできました。
この直角三角形の各辺の長さを以下の図のように\(a, b, c\)と置きます。
直角三角形には色を付けてみました。
では、この大きな正方形の面積を二通りの方法で考えてみましょう。
まずは、大きな正方形の一辺の長さを考えます。
色を付けた四つの正三角形はすべて同じです。
ということは、
このように、
$$\text{大きな正方形の一辺の長さ} = a+b$$
となります。
よって、大きな正方形の面積は、
$$\text{大きな正方形の面積} = (a+b)^2 \tag{1}$$
です。
次に、大きな正方形が、小さな正方形と四つの直角三角形からできていると考えてみましょう。
$$\text{大きな正方形の面積} = \text{小さな正方形の面積} + \text{四つの直角三角形の面積}$$
すると、まず小さな正方形の一辺の長さは\(c\)なので、
$$\text{小さな正方形の面積} = c^2$$
です。
次に、直角三角形の面積は、
$$\text{直角三角形の面積} = \frac{1}{2} ab$$
です。
これらを、大きな正方形の面積の式へ代入すると、
\begin{align}
\text{大きな正方形の面積} & = \text{小さな正方形の面積} + \text{四つの直角三角形の面積} \\
& = c^2 + 4 \times \frac{1}{2} ab \\
& = c^2 + 2ab \tag{2}
\end{align}
です。
ここまで二つの方法で求めた正方形の面積は、同じ正方形であるので等しいはずです。
よって、式(1)と式(2)から、
\begin{align}
(a+b)^2 & = c^2 + 2ab \\
a^2 + 2ab + b^2 & = c^2 + 2ab \\
a^2 + b^2 & = c^2
\end{align}
となり、三平方の定理が導けました。
これが、正方形の中に正方形を描いて三平方の定理を証明する方法です。
スポンサーリンク
正方形と三角形を使った積み木で三平方の定理を証明する方法
次は、正方形を小さな正方形と四つの三角形に分割し、分解した後再び組み立てることで三平方の定理を証明する方法です。
まずは、正方形を用意します。

これを以下のように分割しましょう。

分かりやすく分割した図形に色を付けてみました。
一つの小さな正方形を囲むように、周りには直角三角形が配置されています。
各辺の長さまで描いてしまいましょう。

注意するのは、小さい正方形の一辺の長さが(\(b-a\))となることです。
次に、これらの分解した図形を以下のように組み立てましょう。
すると、次の図のように二つの正方形の組み合わせであることが分かります。
それぞれの正方形の面積を足すと、
$$a^2 + b^2$$
ですが、元々この二つの正方形は、一つの大きな正方形から作られています。
もとになった正方形の一辺の長さは\(c\)であり、面積は\(c^2\)です。
よって、
$$a^2 + b^2 = c^2$$
が成り立つことが分かります。
これで、正方形を小さな正方形と四つの三角形に分割し、分解した後再び組み立てることで三平方の定理を証明する方法は終わりです。
まとめ
- 正方形から三平方の定理を証明する方法を紹介した
- 一つは正方形の中に正方形を描いて証明する方法
- 二つ目は、正方形を分解して二つの正方形にして証明する方法
- 三平方の定理を証明する方法はたーくさんあるが、ここで証明した方法はどちらもシンプルで好き(個人の感想)


























ディスカッション
コメント一覧
まだ、コメントがありません