円の面積はなぜ「π×r×r」なのか？ – 公式の求め方を丁寧に解説
円の面積の公式はなぜ「\(π\)×\(r\)×\(r\)」と表現できるのでしょうか？
ここではそんな疑問に対して、図形を使った簡単な公式のイメージ方法を紹介します。
先に言っておくと、ここで紹介する方法は円の面積の厳密な証明方法ではありません。
厳密な証明を数学チックにするには、最低限高校生の数学知識が必要です。
一方、ここでの方法は小学生でも簡単に納得できる方法となっています。
難しい数式は一切登場しません。
円周率とは何かを知る
まず、円の面積の公式について知る前に、絶対に知っておかなければいけない知識があります。
それは、「円周率(\(3.14\))とは何なのか」ということです。みなさんは、「円周率って何？」と聞かれて答えることができますか？
円周率とは、
円の円周の長さは、直径の何倍であるか
を表す数です。
これがわかっている人は、この章は飛ばしてもらって構いません。「円の面積の公式を求める」の章まで進みましょう。
上の説明で「どゆこと？？？」である人に、円周率を説明しておきます。
例えば、以下のような円があったとします。
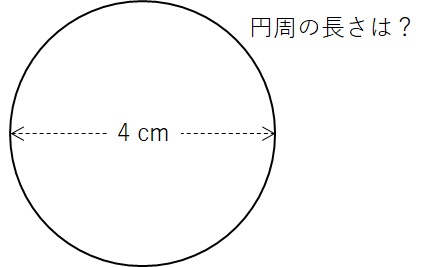
直径が\(4\)cmの円です。
この円の円周の長さはなんでしょうか？
答えを言うと、円周の長さは\(12.57\)cmとなります。
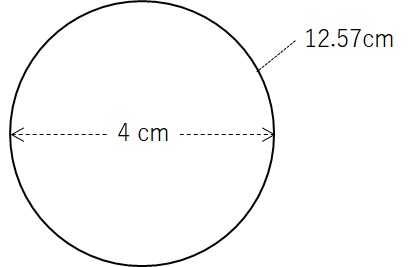
このとき、円周の長さ(\(12.57\)cm)は直径(\(4\)cm)の3.14倍となっています。
$$4\text{cm} \times 3.14 = 12.57\text{cm}$$
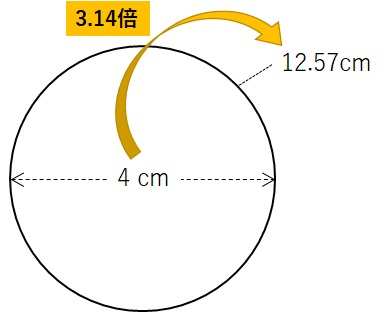
言い換えると、
円の直径に3.14を掛けると、円周の長さ
となるのです。
この3.14のことを円周率と呼びます。
円周率はどんな円でもかならず同じ数（\(3.14\)）になります。
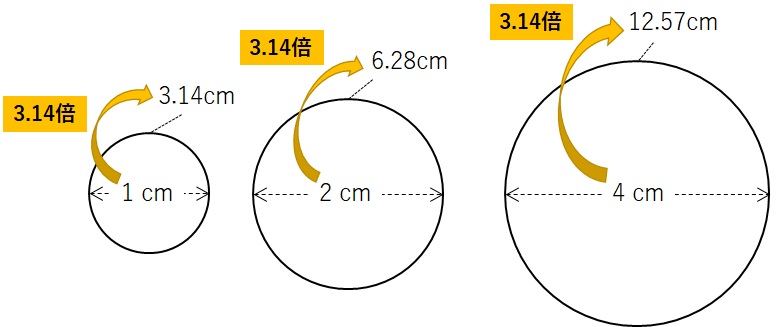
すなわち、円はかならず「直径を3.14倍すると円周の長さ」になるのです。
円周の長さが直径の何倍であるかを表す数
スポンサーリンク
円の面積の公式の求め方
では、本題に入りましょう。なぜ円の面積は、
$$\text{円の面積} = \text{円周率}(3.14) \times \text{半径} \times \text{半径}$$
という公式で表せるのかを考えていきます。
ここからは、円の面積を\(S\)、円の半径を\(r\)、円周の長さを\(l\)として話を進めていきます↓
円を8等分にして並び替える
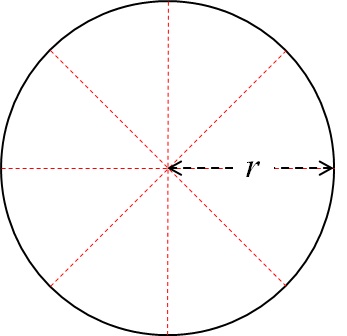
まず、円をいくつかの同じ面積のパーツに分割しましょう。
まさに、ピザを一人前に取り分けるようなやり方です。
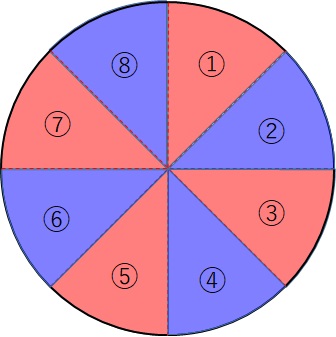
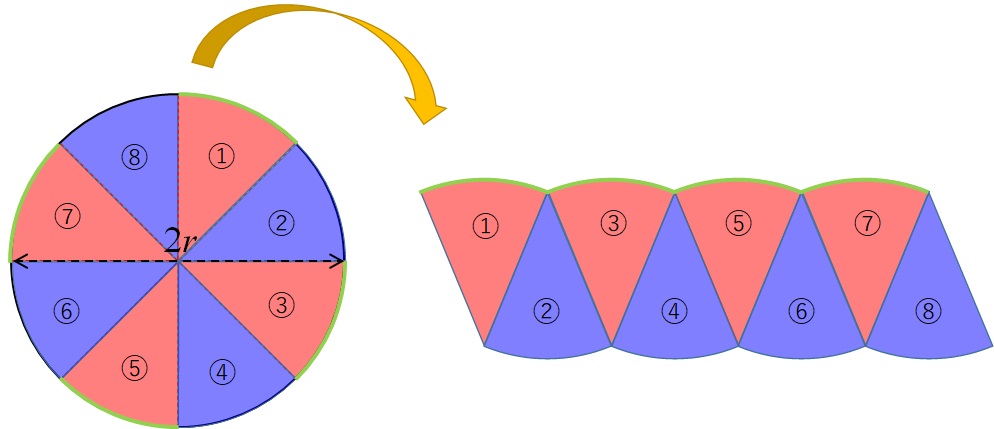
円を8等分してみました。一つ一つのパーツは扇形になっていることがわかります。
今後の操作を分かりやすくするため、分割したパーツに色を付けておきます。
これを以下のように並べ替える↓
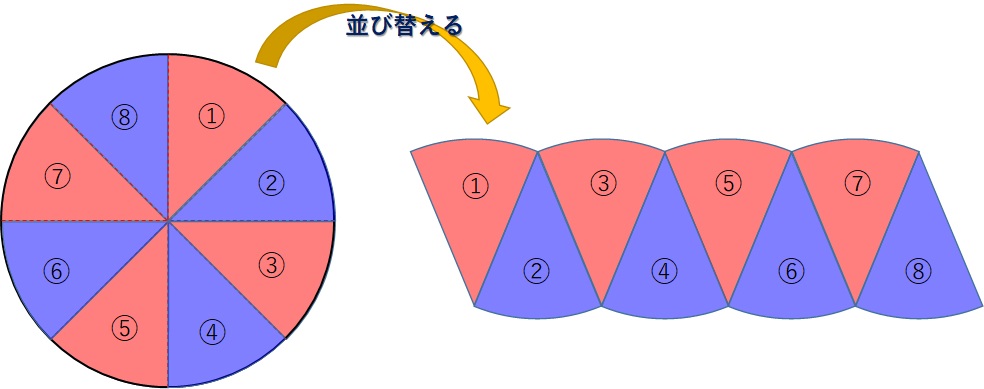
すると、少しだけ長方形に近づきましたね。
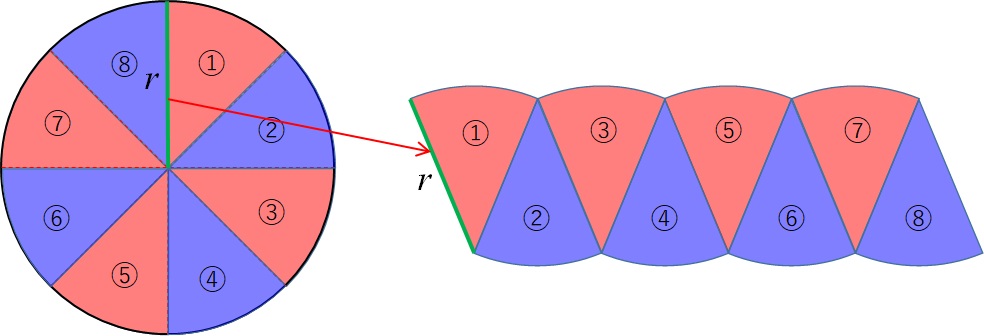
ここで、上辺の長さ（下の図で緑で示した部分）を考えましょう。
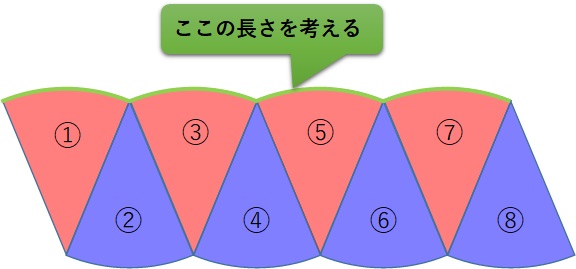
以下の図を見ると、上の辺の長さは、8つに分割した扇形の弧が4つ並んでいます（緑の線で示した部分です）。
ここで、円の半径は\(r\)ですので、直径は\(2r\)です。なので、円周の長さは、
$$\text{円周の長さ} = 2r \times \pi = 2 \pi r$$
となることに注意すると、一つ一つの弧の長さは、円周を8つに分割した長さですので、
$$\text{一つの弧の長さ} = \frac{2 \pi r}{8}$$
と表現できます↓
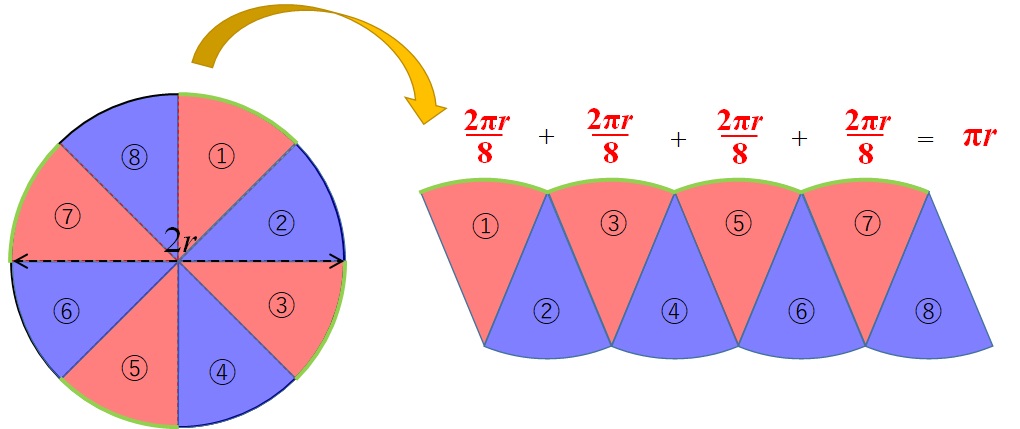
すべてを足して上辺の長さを求めると、\(\pi r\)ですね。
次に、下の図で示す横の長さはどうでしょうか？
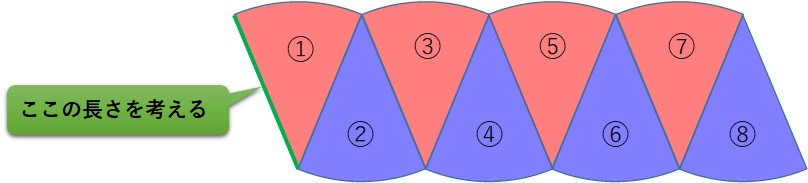
これは、円の半径になっていますね↓
よって、縦と横の長さをまとめると、以下のようになります。
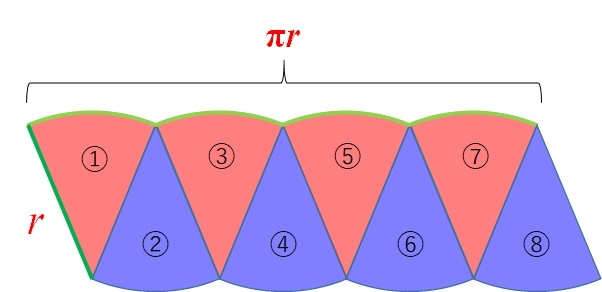
これは、次の長方形にまあまあ近いですね。
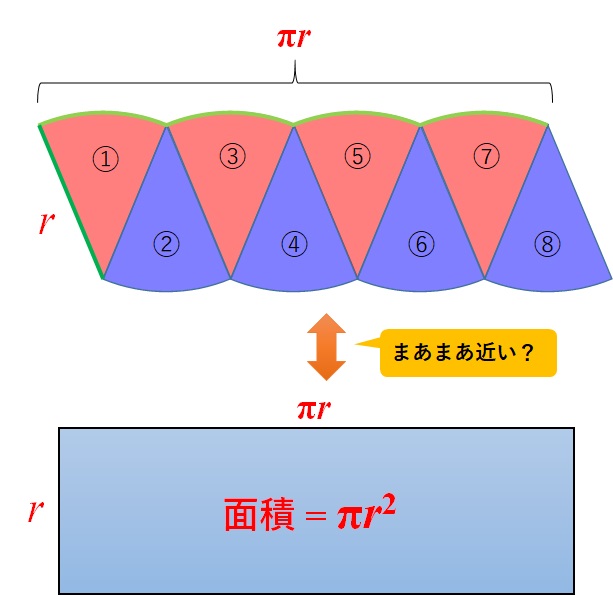
この長方形の面積は\(\pi r^2\)なので、円の面積もおそらくこれに近い値になるのではないかという推測ができます。
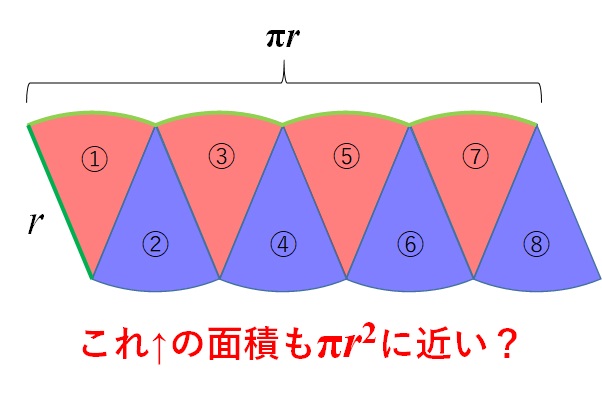
しかし、これではまだまだ、「円の面積は\(\pi r^2\)だ」とはとても断言できませんね。
そこで、もっと細かく円を分割してみましょう。
今は円を8等分していましたが、もっと細かくすることで、上辺がどんどん直線に近づいていくことが予想できます。
円を32等分にして考える
では、次は同じ操作を32等分に分割して行ってみます。
まず、分割すると以下のようになります↓
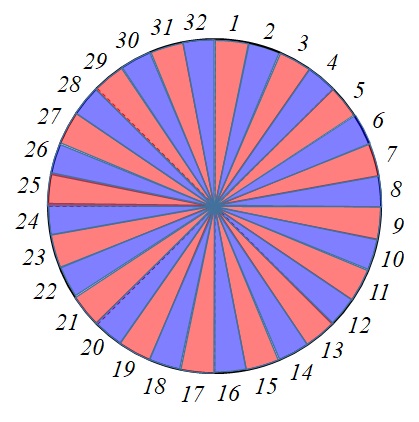
32個の扇形ができました。そして、これを並べ替えると、
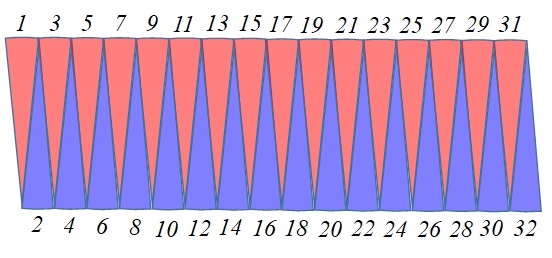
となります。8等分のときよりもかなり長方形に近づきましたね。
上の辺と下の辺の長さは、それぞれ円の半分の弧でできているので、長さは円周の半分となります。
また、横の辺の長さは、円の半径になっていることがわかります。
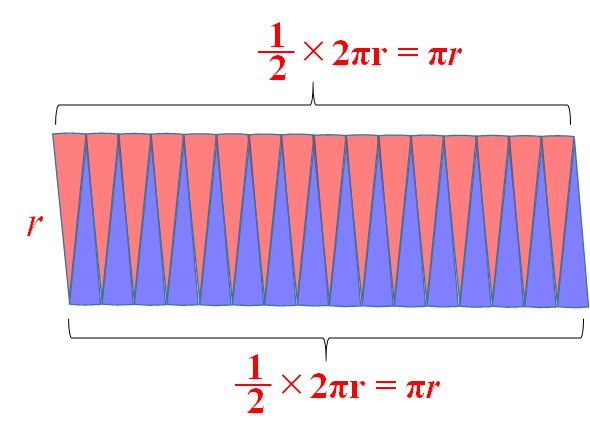
これをほとんど長方形とみなして、「横の辺の長さ(\(\pi r\))×縦の辺の長さ(\(r\))」で面積が求めれるとすれば、
\text{円の面積} = \pi r \times r = \pi r^2
となります。これはみなさんが知っている円の面積の公式となっていますね。
無限に細かく分割する
もちろん、正確な長方形ではないので厳密な証明にはなっていませんが、これがもっともっと細かく分割した扇形を作って同じ操作をすると、限りなく長方形に近づくはずです。
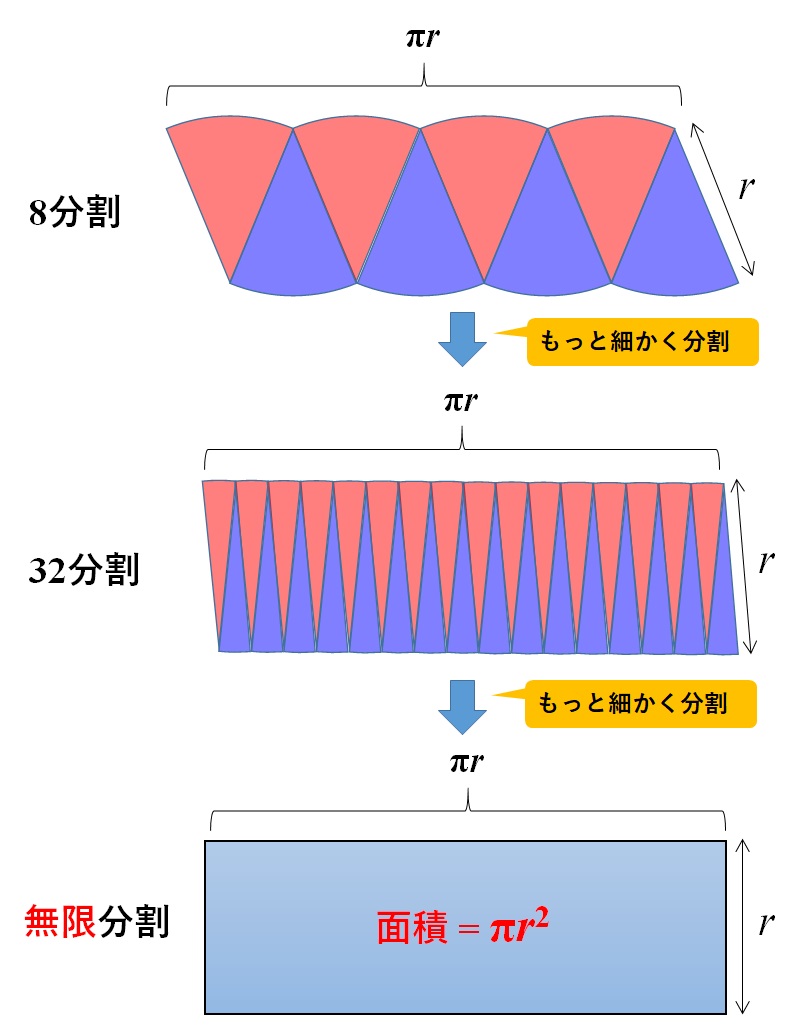
このように、無限分割すれば長方形が現れ、あとは長方形の面積を求めればよいので、
\text{長方形の面積} = \pi r \times r = \pi r^2
となります。この長方形は元は円を分割して作ったものでした。
ですので、「長方形の面積＝円の面積」ですね。よって、
\text{円の面積} = \pi r \times r = \pi r^2
となり、円の面積の公式が求まりました！
まとめ
ここでは、小学生の知識でもわかる円の面積の公式を証明する方法を紹介しました。
その方法とは、ピザを等分するように円を細かく分割し、長方形を作ってその面積を計算するという方法です。
このように、ここでは円を長方形という別の図形にして面積を求める方法を紹介しました。
同じように、円を三角形に変形して面積の公式を求める方法というのも存在します。こちらの方法もすごく面白いのでぜひチェックしてみてください↓
https://analytics-notty.tech/reason-for-consent-that-area-of-circle-be...