\((a+b)^2=a^2+2ab+b^2\)の公式は図形を使えば理解できる!
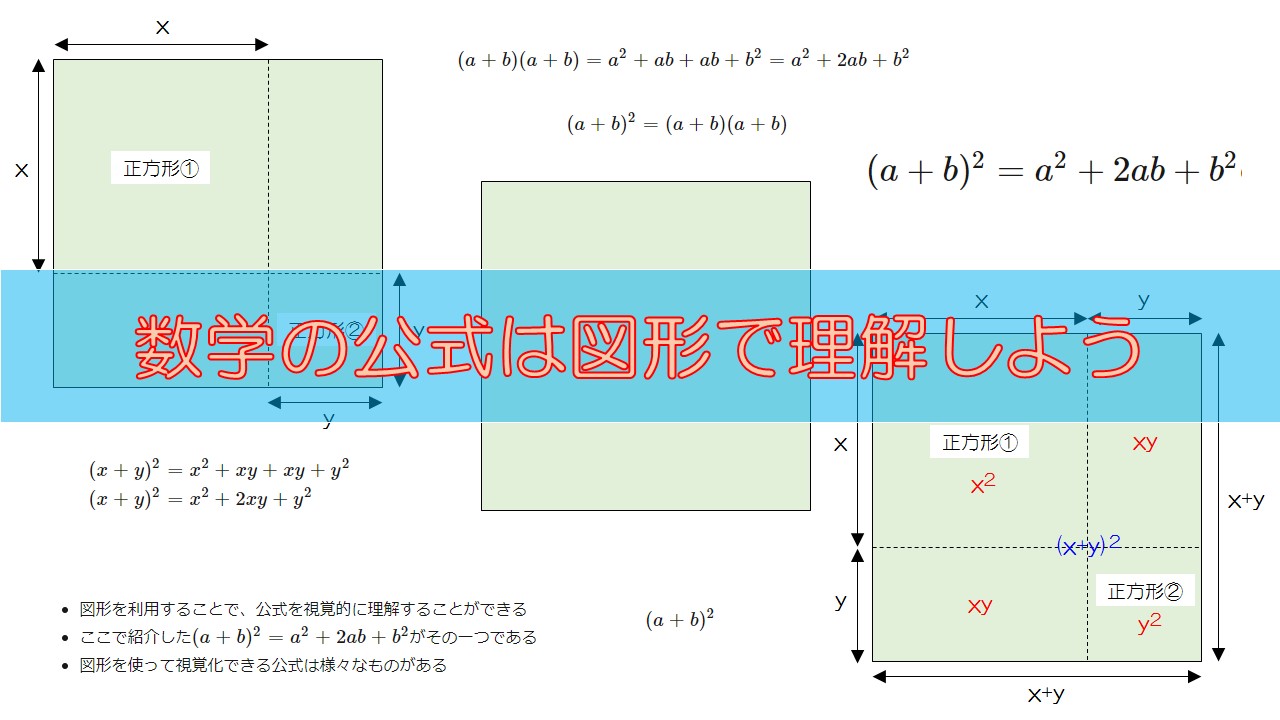
学校では、たんに暗記していた数学の公式ですが、図形を使えばなぜ”その公式が成り立つのか”ということが視覚的に理解できるようになります。
すべてではありませんが、図形で簡単に説明できる公式は実に様々なものがあります。
ここでは、その一つである
$$(a+b)^2=a^2+2ab+b^2$$
を図形を使って説明してみましょう。
(a+b)2=a2+2ab+b2の公式は四角形を書いて理解する
中学校で習う展開の公式に、
$$(a+b)^2=a^2+2ab+b^2$$
というものがあります。
基本の公式なので、みなさん見覚えはあるのではないでしょうか。
しかし、みなさんなぜこの公式が成り立つか考えたことはありますか?
証明は簡単で、左辺の、
$$(a+b)^2$$
を、
$$(a+b)^2 = (a+b)(a+b)$$
として、たすき掛けして計算すれば、
$$(a+b)(a+b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2$$
となり、公式が成り立つことはわかります。
ここでは、この公式の意味を理解しましょう。
これには、図形を使った方法が一番です。
スポンサーリンク
図形を使った証明
図形を使うことは、もっとも視覚的(ビジュアル的)にわかりやすい証明の方法です。
計算なんて必要ありません。ある図形を書くだけで、すぐに公式が成り立つことが分かってしまいます。
その図形とは、”正方形”です。下の図のような感じです。

普通の”正方形”ですね。
これに、いくつかの簡単な操作を行っていくことで、
「あれっ!公式が成り立つことが証明できちゃった!」
となります。
まずは、この正方形を四つの四角形に分割しましょう。下の図のような感じです。
このとき、左上と右下には二つの正方形ができるように分割することがポイントです。それぞれ正方形①、正方形②と呼びましょう。
上の図では、正方形①と②の一辺の長さをそれぞれ、\(x\)と\(y\)としています。
では、上の図に分割した四つの四角形と辺の長さ、そして面積をすべて記述してしまいます。
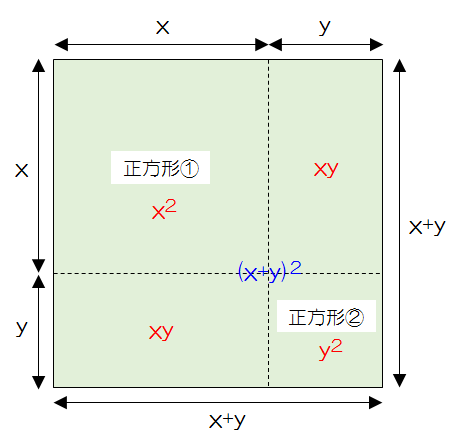
それぞれ、辺の長さを書きましたが、ここで注目するのは、面積です。
赤い色で書いているのが分割後の四角形の面積、青色で書いているのが元の大きな正方形の面積です。
当然、元の大きな正方形の面積と分割後の四角形の面積は同じなはずなので、
\begin{align}
(x+y)^2 & = x^2 + xy + xy + y^2 \\
(x+y)^2 & = x^2 + 2xy + y^2
\end{align}
となります。
なんと、これは初めに見た展開の公式ですね。\(x\)と\(y\)を\(a\)と\(b\)に変えてやれば、初めに見た公式、
$$(a+b)^2=a^2+2ab+b^2$$
になります。
このように、図形を利用すれば、視覚的に公式を理解することができます。
ここで紹介したもの以外にも様々な公式に対して、図形を使って証明・理解できる方法が用意されています。
例えば、
$$x^2 – y^2 = (x+y)(x-y)$$
の公式も図形を使えば、感覚的に理解することができるのです。
興味のある人は、
を見てみてくださいね。
まとめ
- 図形を利用することで、公式を視覚的に理解することができる
- ここで紹介した\((a+b)^2=a^2+2ab+b^2\)がその一つである
- 図形を使って視覚化できる公式は様々なものがある



























ディスカッション
コメント一覧
まだ、コメントがありません