「微分とは何か」をわかりやすく解説 – ”微分は傾き”の意味を理解しよう！
「微分」とは何なのかを丁寧に説明します。微分とは何かをネットなどで調べるとよく「傾きのことだよ」と書いてあります。
数学が得意な友人に聞いても同じような答えが返ってきた。という人もいるかもしれません。しかし、そんなことを一言で言われても「どういうこと？」となってしまいますよね。
そんな悩みを抱えている人はこのページを読むことで、「微分は傾きと同じことである」ということが理解できます。
微分とは？
「微分」とは、何でしょうか？
微分を一言で表現するときに、よく言われるのが、
「微分とは、”傾き”である」
です。
このように言われると、”微分をすでにわかっている人”にとっては「そうだよねー」となります。
しかし、学校で初めて微分を習ったばかりの人が、「微分とは”傾き”だよ」と言われてもピンとこないでしょう。
そこで、このページでは、一つ目の目標として初心者の人に、
「微分は傾き」であることを理解してもらうこと
から始めます。
そして二つ目の目標としては、
頭の中で微分を具体的にイメージできるようになること
を目指します。
- 【ステップ１】「微分は傾き」であることを理解しよう！
- 【ステップ２】頭の中で微分を具体的にイメージできるようになろう！
今日、初めて学校で微分を習った人でもわかるぐらい噛み砕いて説明していきますね。
スポンサーリンク
微分の正式な定義
微分の正式な定義は次のようなものです。
以下の式の\(f(x)^\prime\)を\(f(x)\)の微分という
$$f^\prime (x) = \lim_{h \rightarrow 0} \frac{f(x+h) – f(h)}{h}$$
なんだかわけがわからないですよね。
ここではこんなのは覚えなくていいです。
数学を学ぶとき、難しい式を覚えることはまったく重要ではありません。
大事なことは、式を頭の中でイメージできるかどうかです。イメージさえできていれば、式なんて覚えなくても、全く問題ありません。
「微分」は「傾き」かもしれない…
まずは、「微分と傾きにはなんか関係があるの？」という人に対して、「微分は傾きかもしれない…」と思ってもらうための説明を始めます。
はじめに、”学校で行う微分”について復習しましょう。学校で習う微分は大抵が「微分せよ。」という計算問題です。
例えば、学校では以下のような問題が出題されます。
次の関数を微分せよ。
$$y = x$$
これは、微分をする計算問題の中で一番簡単かもしれません。答えは、
$$y^\prime = 1$$
ですね。よって、\(x\)の微分は\(1\)です。
こんな誰でも解ける問題ですが、なぜ\(x\)を”微分”すると\(1\)になるのかは”微分とは何なのか”を知らないとわかりません。
では次に、傾きについて考えていきましょう。
まず、問題の関数である、
$$y = x$$
をグラフに描いてみます。すると、下の図のようになります。
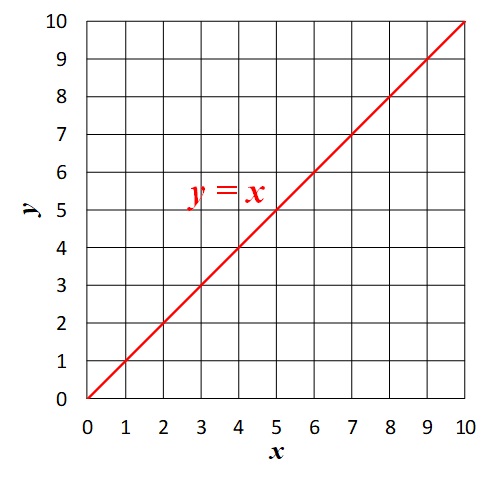
この赤い直線が\(y=x\)です。
では、この直線の傾きは何になるでしょうか？まずは、傾きとは何だったのかを思い出しましょう。中学数学の知識で言うと、
\(x\)が\(1\)だけ増加したときの、\(y\)の増加量
ですね。※厳密にいうとこの表現は正確ではないのですが、まずは中学数学の範囲の知識で説明をしたいため、このような定義とさせてください。
グラフ上で傾きを考えるには、\(x\)方向に\(1\)進んだときに\(y\)方向にどれだけ進むかをみればいいでしょう↓
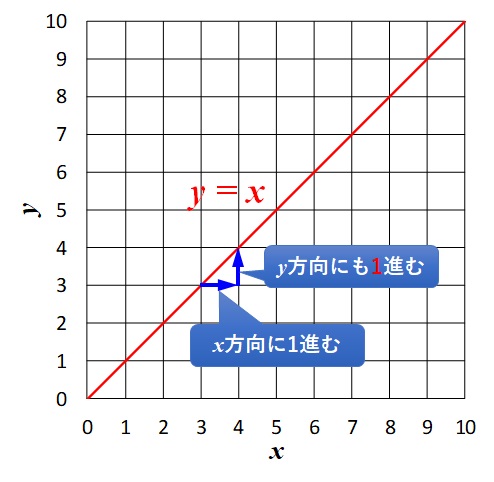
上のグラフから明らかなように、\(x\)が\(1\)だけ進むと\(y\)方向にも\(1\)進んでいます。
よって、\(y=x\)の傾きは\(1\)ということになります。
ここで、微分した値を思い出しましょう。\(y=x\)を微分すると\(y^\prime = 1\)でしたね。\(x\)の微分は\(1\)です。
さっき求めた傾きも\(1\)でした。つまり、いま、
$$x\text{の微分} = x\text{の傾き}$$
が成り立っています。
これは、よく言われている「微分とは傾きだ」という説明そのものですね。やっぱり、微分とは傾きだったのです。
スポンサーリンク
本当に「微分＝傾き」なのか？
「おいおい、ちょっと待ってくれ。今回は偶然だろ？」という声が聞こえてきそうです。
偶然でしょうか？確かに、たまたま今回の式（\(y = x\)）だけ傾きと微分が同じ値になった可能性もありますね。
では、違う関数に対して同じように考えてみましょう。次の関数を考えます↓
$$y = 2 x$$
この式を同じようにグラフにすると、
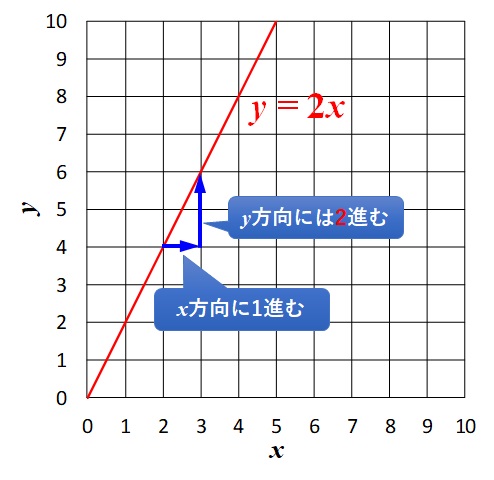
となります。
そして、グラフ中に描いているように、\(x\)が\(1\)だけ増加すると\(y\)は\(2\)増加しますので、この直線の傾きは\(2\)です。
では、\(y=2x\)の微分はなんでしょうか？これも簡単に求まり、\(y^\prime = 2\)ですね。
関数\(y=2x\)も、やっぱり、
$$x\text{の微分} = x\text{の傾き}$$
が成り立つみたいです。
「微分とは、”傾き”である」
は正しいようですね。
「いや、待て！
ここまで考えてきた\(y = x\)や\(y = 2x\)はどちらも直線の式だ。
\(y = x^2\)のような放物線のような曲線を表す式でも”微分=傾き”と言えるのか？！」
と思った人もいるのではないでしょうか？
そんな人はこのまま読み進めましょう。どんな関数に対しても「微分は傾き」であることに納得できるはずです。
本当の傾きを知っておこう！
放物線の式のに進む前に、その準備として知っておかなければならないことがあります。
それは、”本当の傾き”についてです。ここまでは「\(x\)が\(1\)だけ増加したときに\(y\)がどれだけ増加したか」が傾きだと言ってきました↓
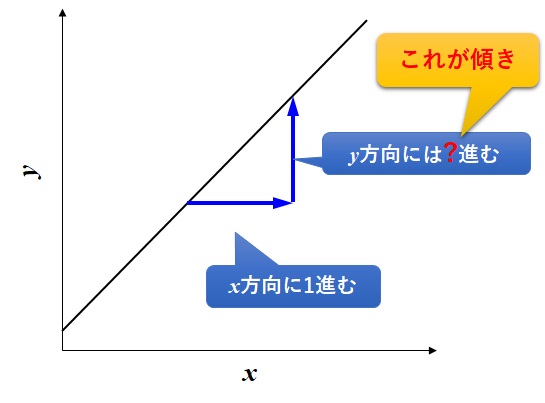
では、下のグラフのような曲線があったとしましょう。
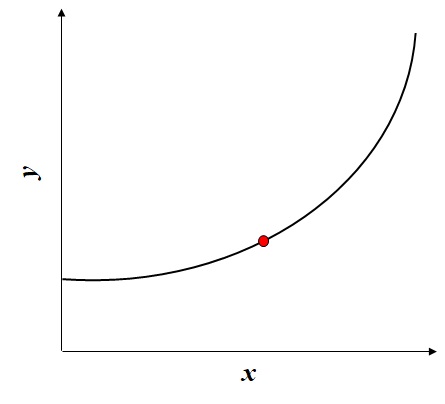
こんなとき、上の赤い点の傾きはどのように調べればよいでしょうか？
これまで通りの方法では、\(x\)が\(1\)だけ増加したときの\(y\)の増加量ですから、下の図のように\(y\)がどれだけ増加しているかを調べればよいでしょうか？
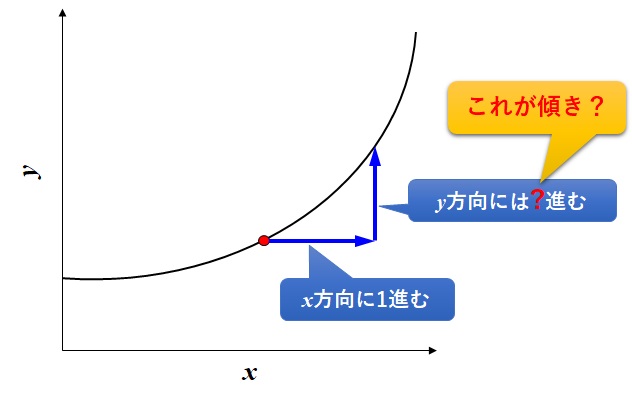
これは、正確な方法ではありません。
本当の傾きとは、次の式で定義されます。
$$\text{傾き} = \frac{y\text{の増加量} }{x\text{の増加量} }$$
※ただし、\(x\)の増加量は十分小さくする。
ここまでに使った傾きの定義は「\(x\)が\(1\)だけ増加したときの\(y\)の増加量が傾き」としていました。
なので、上の定義の「\(x\)の増加量」に\(1\)を入れると、
\begin{align}
\text{傾き} & = \frac{y\text{の増加量}}{1} \\
& = y\text{の増加量}
\end{align}
となるため、\(x\)を\(1\)増加させたときの\(y\)を見て、これを傾きと呼んでいました。
しかし、本当の傾きの定義は「\(x\)が\(1\)だけ増加したとき」ではないんです。
※マークの一文「\(x\)の増加量は十分小さくする。」に注目しましょう。
本当の定義は\(x\)の増加量は\(1\)ではなく、\(x\)の増加量をもっともっと小さくしたときの\(y\)の増加量を見なけれいけません。
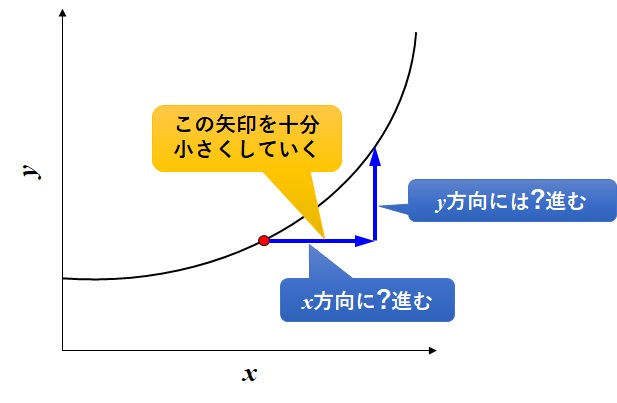
では、いま考えているグラフの赤い点で\(x\)の増加量を小さくしていくとどうなるでしょうか？↓
\(x\)方向への増加を表す矢印がどんどん小さくなっていきますので、赤い点付近をどんどん拡大してきましょう。
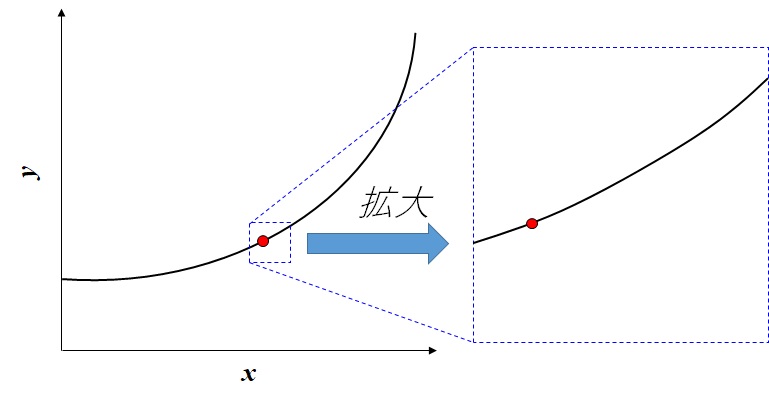
さらにもっと、ずーーーーっと拡大すると、どうのように見えるでしょうか？
それは、下の図のように曲線ではなく、直線に見えてきます。
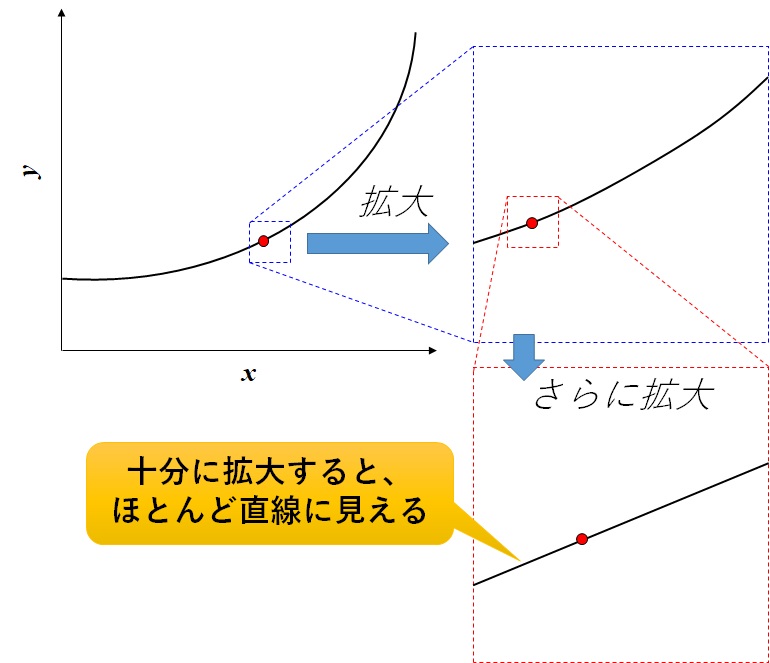
どんな曲線でも十分に拡大すれば（つまり\(x\)の増加量を十分に小さくすれば）、直線に限りなく近づきます。
このように、十分に\(x\)の増加量を小さくしたうえで、\(y\)の増加量を測るのが正式な傾きの定義です。
ですので、十分に小さくした\(x\)の増加量を\(\Delta x\)、そのときの\(y\)の増加量を\(\Delta y\)にすると、傾きの定義は、以下のように書けます。
$$\text{傾き} = \frac{\Delta y}{\Delta x}$$
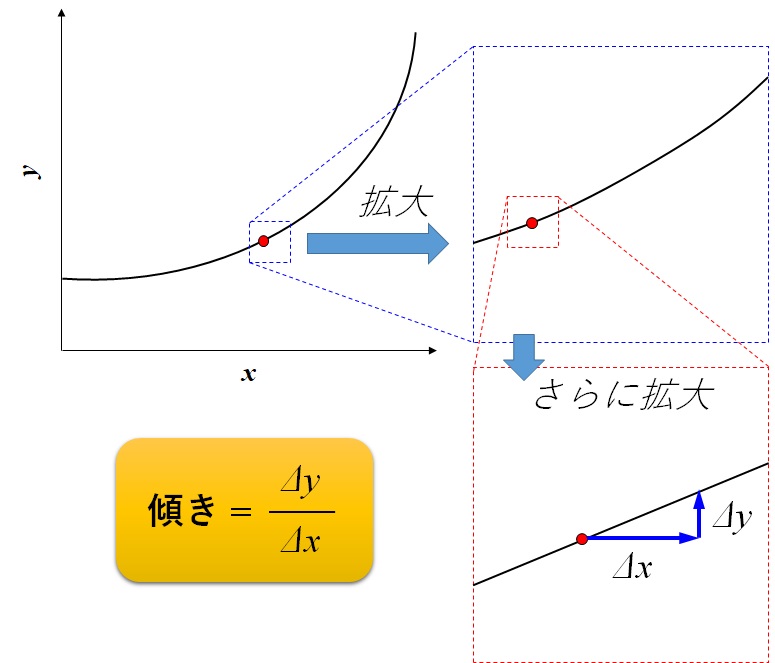
よって、グラフから傾きを求めるステップは、
- 【ステップ①】傾きを求めたい点を決める
- 【ステップ②】その点に向かって、十分に拡大する
- 【ステップ③】ほとんど直線に見えるようになったら、\(\Delta y/\Delta x\)を計算する
です。
このような傾きの求め方を別の表現を使って言うと、
曲線に接する直線に対して、\(x\)を\(1\)だけ増加させたときの\(y\)の増加量
これが傾きとなります。こちらも覚えておきましょう。
スポンサーリンク
\(y=x^2\)の微分
本当の傾きの求め方がわかったところで、直線の式ではなく放物線の式について微分と傾きの関係を調べましょう。次の関数を考えます。
$$y=x^2$$
まずは、これまで通りこの式をグラフ化します↓
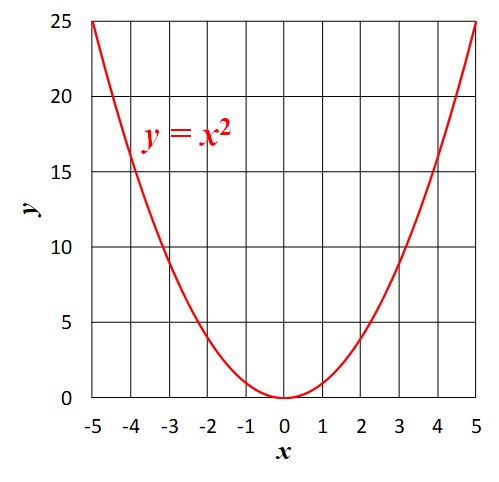
そして、このグラフから\(x\)が\(1\)だけ進んだときの\(y\)の増加量を読み取りましょう。そうすれば、傾きがわかるはずです……
ただ、ここで少し困ったことがあります。今までの直線の式では、どの場所（どの\(x\)でも）で考えても傾きは同じでした。
しかし、今回の放物線の場合は、\(x\)の位置によって傾きが変わってきそうです。
例えば、\(x=1\)での傾きと、\(x=3\)での傾きでは違う値が出てきそうですね。
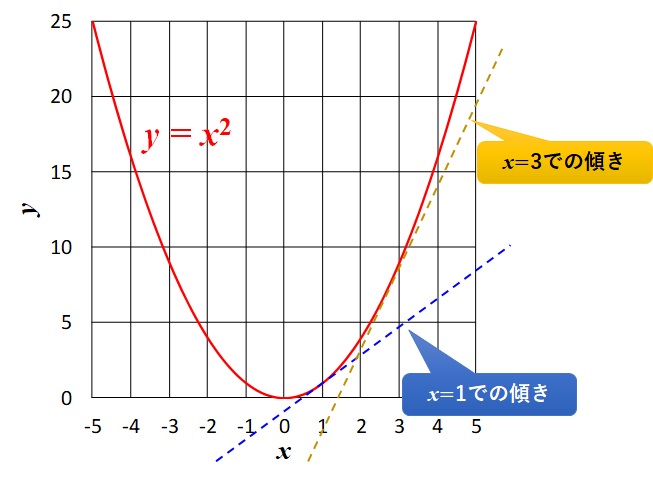
\(x=1\)での傾きに比べて、\(x=3\)での傾きの方が大きそうです。
もっというと、\(x=-3\)と\(x=3\)での傾きは、符号すら違いそうです。
\(x=3\)では、\(x\)が\(1\)だけ増加すると\(y\)は増加しますが、\(x=-3\)では、\(x\)が\(1\)だけ増加すると\(y\)は減少しますからね↓
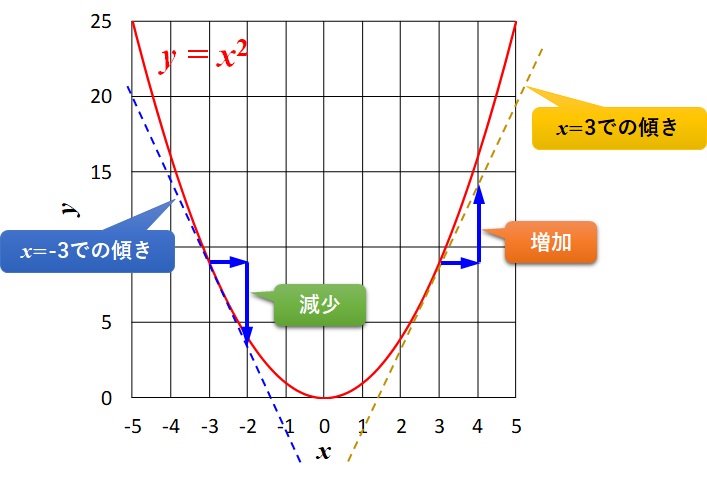
このような状態なので、とりあえず\(x\)が\(x=-3, 1, 3\)のときの3点について傾きを求めてみます。
その前に、傾きの求め方を思い出しておきましょう↓
【ステップ①】傾きを求めたい点を決める
【ステップ②】その点に向かって、十分に拡大する
【ステップ③】ほとんど直線に見えるようになったら、\(\Delta y/\Delta x\)を計算する
でしたね。
\(x=-3\)のときの傾き
\(x=-3\)のときは、\(x\)が増加すると\(y\)は減少します。よって、傾きは負になりそうなことがわかります。
傾きをグラフから求めましょう。まずは、十分直線に見えるくらい拡大するのでしたね。
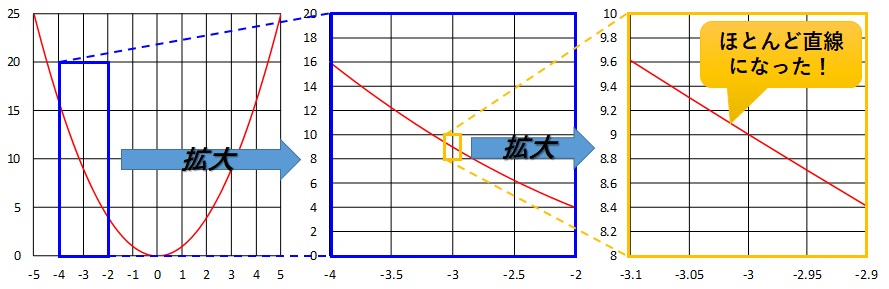
※拡大していくことで、縦軸と横軸の範囲が変化していっていることに注意してください。
一番左の元のグラフから、\(x=3\)付近をどんどん拡大していき十分直線に見えるほど拡大しました。一番右のグラフは、ほとんど直線に見えますね。
ここで、\(\Delta x\)と\(\Delta y\)をグラフから読み取ります↓
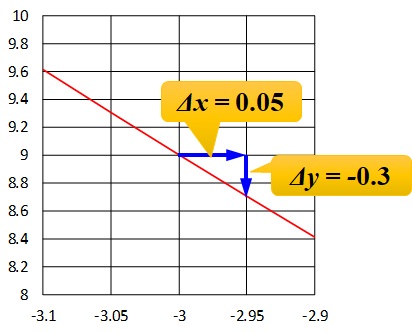
- \(\Delta x = 0.05\)
- \(\Delta y = -0.3\)
ですね。\(\Delta y\)を\(\Delta x\)で割れば傾きが求まります。
$$\frac{\Delta y}{\Delta x} = \frac{-0.3}{0.05} = -6$$
よって、\(x=-3\)のときの傾きは\(-6\)ですね。
\(x=1\)のときの傾き
傾きをグラフから求めましょう。まずは、十分直線に見えるくらい\(x=1\)の付近を拡大します↓
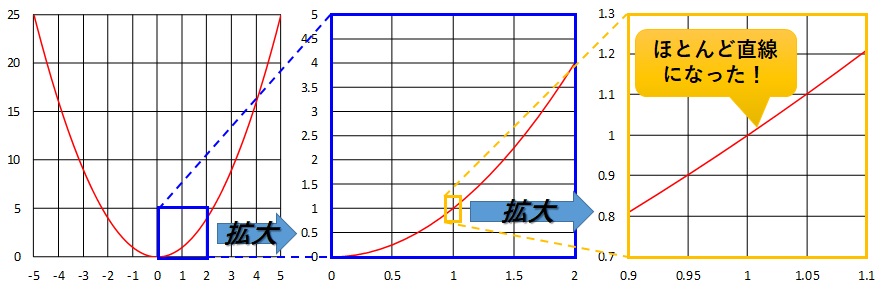
※拡大していくことで、縦軸と横軸の範囲が変化していっていることに注意してください。
一番左の元のグラフから、\(x=1\)付近をどんどん拡大していき十分直線に見えるほど拡大しました。一番右のグラフは、ほとんど直線に見えますね。
そうなったら次は、\(\Delta x\)と\(\Delta y\)をグラフから読み取ります↓
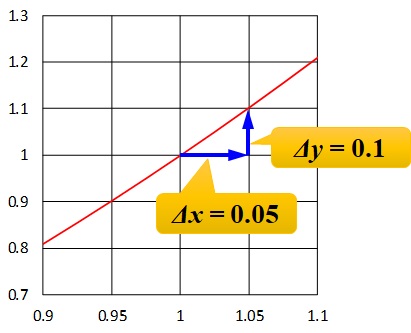
- \(\Delta x = 0.05\)
- \(\Delta y = 0.1\)
ですね。最後に、\(\Delta y\)を\(\Delta x\)で割れば傾きが求まります。
$$\frac{\Delta y}{\Delta x} = \frac{0.1}{0.05} = 2$$
よって、\(x=1\)のときの傾きは\(2\)となりました。
\(x=3\)のときの傾き
最後に\(x=3\)のときです。
傾きをグラフから求めましょう。まずは、十分直線に見えるくらい\(x=3\)の付近を拡大します↓
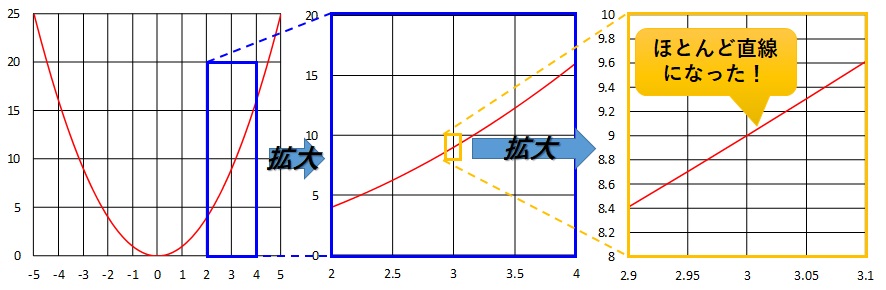
※拡大していくことで、縦軸と横軸の範囲が変化していっていることに注意してください。
一番左の元のグラフから、\(x=3\)付近をどんどん拡大していき十分直線に見えるほど拡大しました。一番右のグラフは、ほとんど直線に見えるほど拡大されました。
そうなったら次は、\(\Delta x\)と\(\Delta y\)をグラフから読み取ります↓
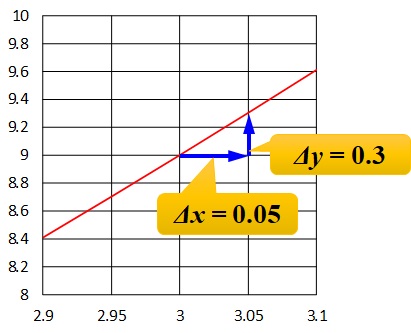
- \(\Delta x = 0.05\)
- \(\Delta y = 0.3\)
ですね。最後に、\(\Delta y\)を\(\Delta x\)で割れば傾きが求まります。
$$\frac{\Delta y}{\Delta x} = \frac{0.3}{0.05} = 6$$
よって、\(x=3\)のときの傾きは\(6\)となりました。
傾きと微分の比較
さて、\(x=-3, 1, 3\)の3点での傾きが求まりましたので、まとめましょう。
\(y = x^2\)の関数において、
- \(x=-3\)のとき、傾きは\(-6\)
- \(x=1\)のとき、傾きは\(2\)
- \(x=3\)のとき、傾きは\(6\)
でした。
これを\(y = x^2\)の微分と比較してみましょう。
\(y = x^2\)の微分は、
$$y^\prime = 2 x$$
です。放物線の式は直線の式と違って、微分しても\(x\)が残りますね。
これが、\(x\)が違うと傾きが違うことを表現しているのです。
では、上の式に\(x=-3, 1, 3\)を入れて微分の値を出すと、
- \(x=-3\)のとき、微分の値は\(-6\)
- \(x=1\)のとき、微分の値は\(2\)
- \(x=3\)のとき、微分の値は\(6\)
ですね。
先ほど求めた傾きの値と見比べてみてください。
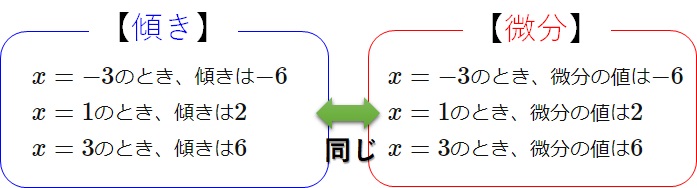
やっぱり、一緒になっていますね。
「”微分”とは、”傾き”」
は納得できましたよね！
微分の漢字に注目してみて！
このように、微分とはすごく小さな範囲を見るとこでした。
”微分”という漢字がそのことをきちんと表現していることがわかります。
二つの漢字で構成されており、それらのイメージは大体以下のようになります。
【微】
ものすごく小さいこと。「微生物」や「顕微鏡」というワードからも、すごく小さいというイメージができると思います。
【分】
分けること。分割や部分といったイメージをもってください。
つまり、微分とは、
すごく小さく分割すること
だったのです。
これはまさに、傾きを求めるときの操作を表していますね。
傾きを求めるときは、すごく小さな範囲を拡大して、その範囲だけの線に注目しました。つまり、すごく小さな領域に分割していたんです。
身近な微分の例
ここまではグラフなどを使って微分をイメージしてきましたが、グラフなんてものは我々の生活には頻繁に登場しません。
「もっと、身近なもので微分を表現してくれないとイメージしづらい！」
という声が聞こえてきそうです。
微分というとどうしても「数学の中だけの世界で、身近な日常には微分は存在しない」と思っている人が大半だと思います。
そんな方に向けて、微分は世界に溢れているんだということをわかってもらえるように、日常生活のどんなところに微分が潜んでいるのかを紹介していきます。
ということで、ここでは我々の生活にある”身近な微分”について紹介しましょう。
例えば、身近な微分の例の一つ目は、「車の速度と走った距離」です。
実は、車が走った距離を微分すると、速度になります。
時速\(60\)kmの車が\(x\)時間走ったとします。そのとき、走った距離\(y\)との関係をグラフにすると、以下の図のようになります。
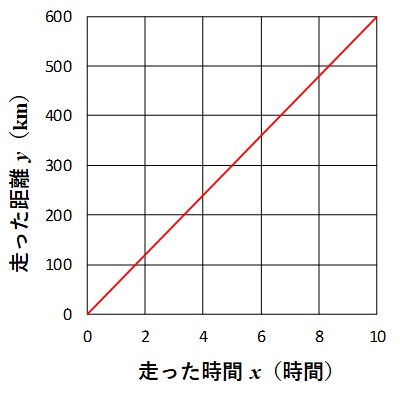
また、
このグラフからわかるように、走った距離\(y\)と走った時間\(x\)は、
$$y = 60 x$$
という関係があることがわかります。
これを微分すると、
$$y^\prime = 60$$
となり、微分は\(60\)です。
これは、車の速度である時速\(60\)kmですね。
つまり、
\text{車の速度} = \text{距離を時間で微分した値}
ということになります。
まとめ
やっぱり、
微分＝傾き
である。
傾きの正式な求め方は、グラフの線を十分に拡大して直線にしてから\(x\)の増加量に対する\(y\)の増加量を調べる。
これは、線を細かく分割してから、その増加量を調べることであり、まさに微分と同じ操作をしていることになる。