面白い数学のパラドックス9選 – 世界は直観では理解できない
数学のパラドックスで、私が特に面白いと感じたものを集めました。
わたしは、どれも騙されてばかりでしたが、あなたはどうでしょうか?
いろいろな数学の分野を紹介していますので、楽しんで行ってくださいね。
- 1. パラドックスとは
- 2. 数学パラドックス①:モンティ・ホール問題 – 一見意味のない行動が実は…
- 3. 数学パラドックス②:誕生日のパラドックス – そんなにいるの?
- 4. ③:1=0.999… – 僅かに1が大きい?いえ、同じです
- 5. ④:景気回復のパラドックス – 景気が回復したのに貧乏人が増える?
- 6. ⑤:全員が借金を返済できる方法 – これをみんなでやれば日本はハッピー
- 7. ⑥:折り紙を何回折れば富士山へ月へ届くでしょう
- 8. ⑦:面積が変化する図形が存在する?!
- 9. ⑧:同じ体毛の数のペアは何人探せば見つかる?
- 10. ⑨:三人の囚人で釈放されるのは誰だ – 囚人の歓喜は正しい?
- 11. まとめ
パラドックスとは
ここでは、数学のパラドックスについて紹介していますが、そもそもパラドックスとは何なのでしょうか?
ウィキペディアによれば、
パラドックス(paradox)とは、正しそうに見える前提と、妥当に見える推論から、受け入れがたい結論が得られる事を指す言葉である。逆説、背理、逆理とも言われる。
とあります。
正しそうに思えることが、実際調べてみたら事実はまったく違った結果だったということですね。
これは言い換えると、
人間の直感は当てにならない
ということです。
では、数学の世界において人間の直感がどれほど当てにならないかを実感していきましょう。
スポンサーリンク
数学パラドックス①:モンティ・ホール問題 – 一見意味のない行動が実は…
背景 – 全米が注目した有名な問題
今や一番有名な数学のパラドックスかもしれません。
”モンティ・ホール問題”
です。
これは、アメリカのテレビ番組で放映された数学の確率に関する問題です。
そのときの司会者がモンティ・ホール氏だったためこのような名前がつけられています。
この問題が世に知れ渡ったとき、アメリカ中が注目しました。
それは、当時世界で一番IQが高い人物でギネス記録にも載っていたマリリンという女性が、この問題に対して自分の答えを言ったところ、多数の数学者から「その答えは間違っている!」、「早々に自分の間違いを認めるべきだ!」など酷いバッシングを受けたからです。
「数学者ではないが、世界一のIQの持ち主が間違えているのか?」
「大学や研究機関で数学を研究している数学者が間違っているのか?」
その結末はどうだったのでしょう。
この問題が有名になった理由は、数学が身近にない普通の人達でも問題自体は簡単に理解できてしまうということです。
さあ、問題を見てみましょう。本当に簡単です!
問題 – モンティ・ホール問題
あなたはクイズ番組に挑戦者として出演しています。
あなたの相手は番組の司会者であるモンティ・ホール氏です。
ホール氏は言います。
ホール氏:「ここに三つのドアがあります。どれか一つのドアの向こうには車があります。それを当てれば車を差し上げましょう。アタリです。」
ホール氏:「ただし、他の二つのドアの向こうにはヤギがいます。ヤギのドアを開けてしまったらハズレです。」
ホール氏:「ドアを一つ選んでください。」
何も情報がない状態であなたは一つのドアを選びます。何も情報がないのですから、当然ここで選んだドアがアタリである確率は1/3です。
すると、司会者のホール氏があなたの選んでないドアでハズレのドアを開けてしまいました。
そして、こう言います。
ホール氏:「このドアはハズレです。」
ホール氏:「もう一度、ドアを選びなおすチャンスをあげましょう。」
ホール氏:「開けるドアを変えますか?そえとも、今選んでいるドアのままでよいですか?」
さて、あなたがアタリを選ぶためには、ドアを変えた方がよいでしょうか?それとも変えなくてもよいでしょか?
どうでしょうか?問題はとても簡単に理解できますよね?
しかし、この問題が全米を大きく騒がせたのです。
みなさんも考えてみてくださいね。正解と詳しい解説は以下の記事をご覧ください。
数学パラドックス②:誕生日のパラドックス – そんなにいるの?
”誕生日のパラドックス”と呼ばれるものです。
私の小学校や中学校は男女20人ずつの40人クラスでした。
40人の中に同じ誕生日のペアがいる確率はどのくらいでしょう?
という問題です。
一年は365日ですので、自分と同じ誕生日の人に出会うのは難しいですよね。
私は今までで自分と同じ誕生日の人に出会ったことはありません。(一日違いの人には会ったことがありますが)
これを考えると、同じクラスに同じ誕生日のペアがいる確率はかなり低そうです…
実際はどうなのでしょうね。みなさんも予想してみてから、以下の記事をお読みください。
これぞまさに、人間の直感があてにならないということを知るための優良な数学パラドックスですね。
スポンサーリンク
③:1=0.999… – 僅かに1が大きい?いえ、同じです
学校では教わらない数学を紹介します。
みなさん、次の二つの数字を見てください。
$$1, \qquad 0.999\cdots$$
\(0.999\cdots\)は無限に\(9\)が続いていきます。
この二つの数字で大きい方はどっちだと思いますか?(見出しでネタばれしてますが…)
多くの人は「\(1\)の方が大きいやろ」と答えるでしょう。
しかし、実は、
この二つの数字の大きさは同じ
なんです。
その証明を以下の記事で紹介しています。算数レベルの計算で証明できてしまいますよ。
これは、”本当は同じではないけど、証明に何かトリックを仕掛けて同じに見せている”というものではなく、数学上、本当に同じ数なのです。
これぞまさに人間の直感が信じれないことの代表的なパラドックスなのではないでしょうか?
みなさんも是非、「\(1\text{と}0.999\cdots\)はどっちが大きい?」と友達に質問してみてください。
おそらく、「\(1\)やろ。」と答えるでしょう。私がそうでしたから(笑)。
④:景気回復のパラドックス – 景気が回復したのに貧乏人が増える?
”景気がよくなった”というニュースに騙されるな
景気のニュースはいつもテレビから流れていますね。それだけみんな景気には注目しているのでしょう。
当然、景気は良い方が私たちにとってはうれしいことですよね。
しかし、景気の状況を調べるとき、そこには数学的なトリックが潜んでいることを忘れてはいけません。
平均値には落とし穴が潜んでいる
例えば、テレビから次のようなニュースが流れてきました。
今年の所得は100~500万円、500~1000万円、1000万円以上のどの所得帯でも、5年前と比べると所得の平均値は上がっています。日本の景気は良くなっているようです。
つまり、日本の所得階層を低層(100~500万円)、中層(100~500万円)、高層(1000万円以上)に分けて、それぞれの階層で平均値を取っているのです。
- 低層(100~500万円)での平均
- 中層(500~1000万円)での平均
- 高層(1000万円以上)での平均
そして、これら三つの層すべてで平均値が上がったということです。
- 低層(100~500万円)での平均 → 上昇
- 中層(500~1000万円)での平均 → 上昇
- 高層(1000万円以上)での平均 → 上昇
ということは、平均したら日本の人々の平均年収が上がったということなので、”景気が回復した”と言えるじゃないか。
ということですね。
これは、正しそうに思えます。
しかし、普段私たちが使っている平均という操作には、大きな落とし穴が潜んでいることも多いのです。
それがまさにここで紹介した景気の話の中に存在します。その落とし穴について詳しく知りたい方は、以下の記事へどうぞ。
スポンサーリンク
⑤:全員が借金を返済できる方法 – これをみんなでやれば日本はハッピー
全員が借金を返済できる方法があったらどうでしょうか?
しかも、誰も損しません。
お金を借りている人は、もちろん借金が無くなりますし、お金を貸している人もちゃんと貸していたお金が返ってきます。
その方法の良いところは非常にシンプルであることです。
何も複雑なことはしません。”借金している人が、お金を貸してくれている人にお金を返す”それだけです。
これで日本もみんながハッピーですね。
どんな方法かは、以下の記事をご覧ください。
紹介している物語の中でみんなが借金を返してハッピーになっていますよ。
…もちろん、罠があります(残念)。
⑥:折り紙を何回折れば富士山へ月へ届くでしょう
いきなり質問です。
一枚の紙があります。この紙を何回折れば、スカイツリーへ、富士山へ、月へ、そして太陽へ届くでしょう?
人間の直感を裏切る有名な質問ですが、まだ知らない人は考えてみてくださいね。
紙は厚みがないと言っていいほど薄いものですよね。

1枚の紙を折っていくと徐々に厚くなってはいきますが、これをスカイツリーや富士山までの高さにするなんて、ものすごい回数を折らないといけないでしょう。
まして月や太陽まで届くまで折るなんて、何億回、何兆回折ればいいの?って感じではないでしょうか?
実際に折ることは不可能ですが、計算は可能です。
以下の記事では、何回折れば富士山まで届くか、月まで届くかを計算しています。
さて、何回折ればいいのでしょうか?きっと意外な結果が待っていますよ↑
⑦:面積が変化する図形が存在する?!
一枚の折り紙があったとします。
これを自由にハサミで切って面積を増やしてください。

できますか?普通はできないですよね。
でもこれができてしまう方法があるんです。
この方法を使えば、面積を減らしたり、そして増やしたりもできます。
…ということは!
食パンにこの方法を使えば、永遠になくならないではないですか!

永遠に食べ続けることができますね。
さて、どんな方法でしょうか?以下の記事をご覧ください。
一見、どこもおかしくなさそうに見えてもどこかに落とし穴があるのですね。
まさに、パラドックスです。
⑧:同じ体毛の数のペアは何人探せば見つかる?
人間の体毛の数は約500万本と言われています。
では、ここに3000人集めました。

この人たちの中で同じ体毛の数のペアはいるでしょうか?
いないと思った人は、何人ぐらい集めれば同じ体毛のペアができると思いますか?
この問題を考える上で便利な式があります。
ペアがいる確率が50%になるためには、どのくらいの数が必要であるかを計算してくれる式です。
それは、
$$1.18\sqrt{n}$$
で計算できるのです。ここで、\(n\)は選択肢の数です。
例えば、上で紹介したように同じクラスに誕生日のペアがいるための人数を考えてみましょう。
ここでの選択肢は”誕生日”なので、選択肢の数は\(365\)ですね。
これを\(n\)に代入します。すると、
$$1.18\sqrt{365} = 22.54$$
となり、約\(23\)となりました。
ということは、「同じクラスに誕生日のペアが50%の確率でいるための人数は23人」ということになります。
ですので、40人のクラスであれば、”ほぼ確実に同じ誕生日のペアがいるはずである”と分かるのです。
では、体毛について考えてみましょう。
はじめに述べたように人間の体毛は約500万本です。このうち、個人差がありますから、人によって400万本~600万本の間で変化するとしましょう。
ということは、選択肢の数は、200万本とします。これを上の式に代入すると、
$$1.18\sqrt{2,000,000} = 1668.772$$
となり、おおよそ1669人です。
1669人いれば、同じ体毛のペアがいる確率が50%なのです。
ということは、3000人の人が集まれば、この中に同じ体毛のペアはほぼ確実に存在します。
以外に少ないと思いませんでしたか?
ライブや成人式などはもっと多くの人が集まりますから、間違いなくペアがいるでしょう。
こんどそのような会に出席するときは、この記事を思い出してくださいね。
⑨:三人の囚人で釈放されるのは誰だ – 囚人の歓喜は正しい?
数学の確率に関するパラドックスには、なぜか囚人が登場する問題が多いのですが、ここで紹介するパラドックスも三人の囚人が登場します。
では、さっそく問題を見ていきましょう。
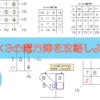
ここに三人の死刑囚がいました。これらの囚人をA, B, Cとしましょう。

この中から恩赦により一人だけ、釈放されることになりました。
釈放される確率は三人とも同じで、\(1/3\)です。

ここで、囚人Aが看守を呼び止め質問をします。
「囚人Bと囚人Cの一人だけでいいので、どっちが死刑(釈放なし)になるのか教えてくれないか?
別に自分のことを聞いているわけではないし、どっちが死刑と聞いたところで自分のことは分からないからいいだろ?」
すると看守は、「それもそうだな」と納得し、
「囚人Bは釈放なしの死刑だよ」
と答えます。
それを聞いた囚人Aは内心、喜びます。囚人Aはこう考えたのでした。
「囚人Bが死刑ということは、俺(囚人A)か囚人Cが釈放だ。釈放の確率が\(1/3\)から\(1/2\)に上がったぞ!」
さて、この囚人Aの考えは正しいのでしょうか?
どうでしょうか?
もともと囚人達が釈放になる確率は\(1/3\)であり、そこから囚人Bの死刑が分かります。
ということは、囚人Aと囚人Bのどちらかが釈放となり、確率は\(1/2\)に上がったような気がしますね。
この囚人Aの歓喜は正しいものだったのでしょうか?
続きは、以下の記事をご覧ください。
まとめ
- 数学パラドックスとは、人間の直観を裏切る数学的に正しい結果である
- ここでは、数学パラドックスを9つ紹介した
- モンティ・ホール問題
- 誕生日のパラドックス
- 1=0.999…
- 景気回復のパラドックス
- 全員が借金を返済できる方法
- 折り紙を何回折れば富士山へ月へ届くでしょう
- 面積が変化する図形が存在する?!
- 同じ体毛の数のペアは何人探せば見つかる?
- 三人の囚人で釈放されるのは誰だ – 囚人の歓喜は正しい?
- どれも面白いものばかりなので、ぜひ友達と考えてみてね!


































ディスカッション
コメント一覧
頭良すぎ!!!!!!!!!!!!!!!!!
( ̄Д ̄)ノ
なるほど!
すごいですね!
4.景気回復のパラドックス に誤記が有ります。
誤:
低層(100~500万円)、中層(100~500万円)、1000万円以上に分けて、
中層(100~500万円)での平均
中層(100~500万円)での平均 → 上昇
正:
低層(100~500万円)、中層(500~1000万円)、1000万円以上に分けて、
中層(500~1000万円)での平均
中層(500~1000万円)での平均 → 上昇
ご指摘ありがとうございます。修正いたしました。
5.全員が借金を返済できる方法 の解説ページへのリンク先が間違っています。
平均値の嘘へ行きます。
間違いを教えていただきありがとうございます。
修正しました。また、何かありましらたご指摘いただくと幸いです。
全員が借金を返せる方法に罠があるならおまえ人間としておかしい
1=0.9999…は数ⅲの極限
面積が変わる図形がある!?のパラドックスに、食パンが増えると記載されていますが実際に飛ぶのは三角形の面積が変わる(減る)やり方を解説しているサイトです。
増やすやり方が知りたいのに減らすやり方を知っても意味が無いので、修正よろしくお願いします。
1=0.999999….
「困難は分割せよ」というデカルトの格言があるけど、世の中にある複雑な現象も、丁寧に解きほぐすと単純な問題の組み合わせでしかないことも多い。それらを理詰めに解き進めていけば、全く手も足も出なさそうな難問でも十分理解の範疇に収まってしまう(こういう発想を還元主義という)。
ただ、「理論が日常的感覚と一致しませんよね?」だけで話を終わらせるのは好きじゃなくて、なぜ一致しないのか、どうすれば一致するのかを解き明かして芋づる式に理解することで、あらゆる理詰めの知識を直感と接続させたいんだよな。そうしないと日常や人生と切り離された場所に閉じた理路が浮いてることになるので、それは個人的に好きじゃない。
単にぺけで済ますのではなく、人間の直感はなぜ当てにならないのか?そんなことを考えると、レトリックや詭弁術とか、それを支える我々の認知バイアスとか、あるいはそういう思考の癖がなぜ形成されたのかという進化心理学にも関心が広がる。
とてもいいので
PIEの秘密も入れてみてはどうでしょうか.
とても面白いのですが、囚人のパラドックスで囚人Aが質問して看守が答える場面がありますが、囚人Aが一人だけ教えてと言っているのになぜ囚人Bや囚人cの場合は2人いたりして、2人いると答えるのですか?意味がわからないです...
だって囚人Aが釈放される時は2人答えられるみたいに書いてありますが、
1人だけと聞いているので...
ということで返信お願いします。
返信きたらすぐ見ます...
PIEの秘密も入れてみてはどうでしょうか.
とても面白いのですが、囚人のパラドックスで囚人Aが質問して看守が答える場面がありますが、囚人Aが一人だけ教えてと言っているのになぜ囚人Bや囚人cの場合は2人いたりして、2人いると答えるのですか?意味がわからないです...
だって囚人Aが釈放される時は2人答えられるみたいに書いてありますが、
1人だけと聞いているので...
ということで返信お願いします。
返信きたらすぐ見ます...
全員借金50万円って流石にあり得ないと思うんですが
あり得たら本当にすごいですね...
あと利子とかはないんですか?
食パンって元々重さも種類によって違うけど
無限に食べ続けれるんだったらどんな食べ物でもいけるのではないでしょうか...
なんて言ってますが不可能なんですか?可能なんですか?
教えてください。
1の「モンティ・ホール問題」と9の「3人の囚人の問題」は実質的に同じ問題なのでは?
ギャンブルやゲームで確率論かじった程度なんですが、
乱数が期待値に収束するのは宇宙が一つである場合だと思う。
選択によって世界が増える多重の平行宇宙だったら乱数が偏り続けて期待値に収束しなくなる可能性がある。
自分はマルチユニバースがあると思ってるんで確率論は信じてないw
あと、ギャンブル理論には無限の試行回数の果てに乱数は期待値に収束するから期待値の高い台でパチンコを打てば短期的に損が出ても長期的に儲かるという理屈があったりするんですが。
現実には無限の試行回数なんて不可能で、試行回数は必ず有限になる。
現実的な意味では確率の正しさなんてそんなもんです。
宇宙が一つでも、試行回数は有限だから乱数は偏る。
我々の人生は確率論的な正しさよりも乱数の偏りの中にあると思う。だから直観は直観で正しい。