紙を何回折ると富士山へとどく？宇宙へとどく？
折り紙はみなさん経験があると思います。その折り紙を何回も折っていくと、どんどん厚みが増していき、高くなっていきますよね。
今回は、紙を何回折るとどのくらいの高さになるかを調べていきます。
ところで、数学に関して、専門家がこう述べています。
「数学に関する人間の直観はあてにならない、それは私のような数学の専門家でもだ」
専門家でも数学というものを直観的に考えると間違えてしまうのですから、私のような一般人はなおさらですね。
ここで考えることは、そのような直観と実際の現象が大きく異なっているという例となります。
では、折り紙を何回折ると富士山や月、宇宙へ届くかということについて考えてみましょう。
折り紙を何回折ったら富士山へとどく？月へとどく？
皆さんは折り紙を折ったことがありますか？
わたしも小学校のときには、鶴を折ったりして楽しんでました。
はじめは薄っぺらい正方形の紙が、折っていくにつれて厚みをもった複雑な形へと変わっていく様子が面白いですよね。
折れば折るほど厚みを増していく折り紙ですが、
厚みが宇宙や月そして太陽まで届くには何回折ったらいいのでしょうか？
想像してみましょう。数万回、それとも数百万回？もっとでしょうか？
実際に折って確かめたいところですが、そんなことは不可能なことはわかっているので、計算によって確認してみましょう。
ちなみに、富士山の標高は3,776m、月までの距離は384,400km、太陽までの距離は149,600,000kmです。
- 富士山までの距離=3,776m
- 月までの距離=384,400km
- 太陽までの距離=149,600,000km
宇宙までの距離も考えたいところですが、地球の大気圏と宇宙の間に明確な境界線があるわけではなく、徐々に大気圏から宇宙になっていくものです。
ですので、色々な意見はあるとは思いますが、ここでは宇宙航空研究開発機構（JAXA）のホームページの
「一般的には空気がほとんどなくなる100kmから先を宇宙」
という記載を採用して宇宙までの距離は100kmとしましょう。
- 宇宙までの距離=100km
なので、今回考える距離をまとめると、
- 富士山までの距離=3,776m ※単位はこれだけmであることに注意
- 宇宙までの距離=100km
- 月までの距離=384,400km
- 太陽までの距離=149,600,000km
です。
スポンサーリンク
紙を折って折って折りまくる
では、計算上ですが、実際に折っていきましょう。
まずは、用意する紙の厚さを調べます。かなり薄いですよね。調べたところ0.08mmという厚さのようです。
予想よりかなり薄かったです。1mmを10分の1したものよりも、さらに薄い厚さようです。これでは月に達するには、かなりの回数折らないといけないのではないでしょうか。
はじめに0.08mmの単位をmに直しておきましょう。
$$0.08mm = 0.00008m$$
となります。折ってない状態で”\(0.00008m\)”です。
一回折ると、その二倍になりますね。実際に折ってみると分かりますが、紙が二枚重なっている状態です。ですので、折り紙の厚さは、
$$0.00008m + 0.00008m = 0.00016m$$
となります。もう一度、二つに折れば、”\(0.00016m\)”の二倍です。
$$0.00016m + 0.00016m = 0.00032m$$
もう一度折ると、”\(0.00016m\)”の二倍です……。
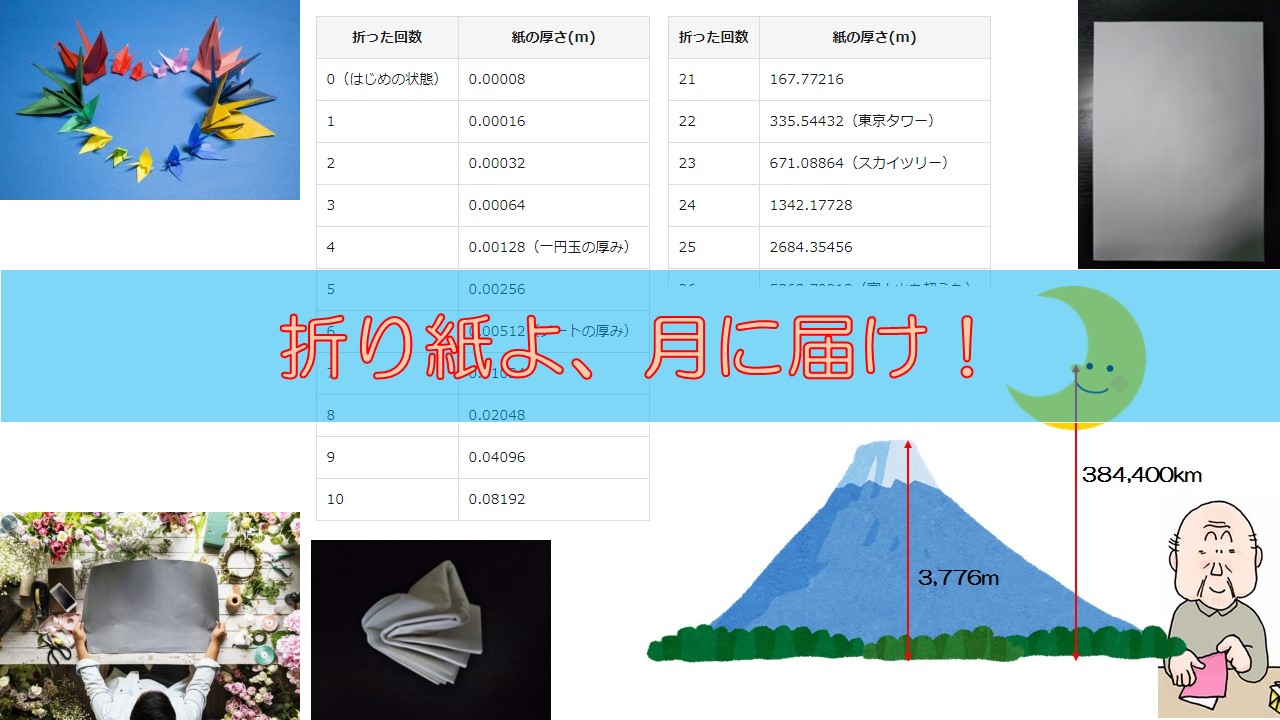
こんな感じで折っていき、10回折ったときの回数と、紙の厚さを下の表にまとめました。単位がmでは、いまいちイメージできないのでcm単位でも表示している。
| 折った回数 | 紙の厚さ(m) |
|---|---|
| 0（はじめの状態） | 0.00008 (0.008cm) |
| 1 | 0.00016 (0.016cm) |
| 2 | 0.00032 (0.032cm) |
| 3 | 0.00064 (0.064cm) |
| 4 | 0.00128 (0.128cm)（一円玉の厚み） |
| 5 | 0.00256 (0.256cm) |
| 6 | 0.00512 (0.512cm)（ノートの厚み） |
| 7 | 0.01024 (1.024cm) ここでようやく1cmを超えた |
| 8 | 0.02048 (2.048cm) |
| 9 | 0.04096 (4.096cm) |
| 10 | 0.08192 (8.192cm) |
10回折り終わりました。
振り返って表を見てみると、4回折った時点で、一円玉の厚みとほぼ同様の厚さとなっています。
また、6回目でノード一冊の厚みとなりました。ノードの紙の枚数は通常は30枚程度です。一方6回折った紙は、64枚（計算方法は後に解説します）であり、だいたい同程度となっています。
10回目が折り終わって、ようやく約0.082m=約8.2cmです。宇宙や月まではまだまだですね。
やっぱり、数万回以上は折らないとダメなんでしょうか？
人間の身長を超えた！
さらに10回折って、合計で20回折ってみましょう。下の表は単位がmであることに注意してくださいね。
| 折った回数 | 紙の厚さ(m) |
|---|---|
| 11 | 0.16384 |
| 12 | 0.32768 |
| 13 | 0.65536 |
| 14 | 1.31072（小学6年生男子の平均身長） |
| 15 | 2.62144 |
| 16 | 5.24288 |
| 17 | 10.48576 |
| 18 | 20.97152 |
| 19 | 41.94304 |
| 20 | 83.88608 |
ここからいっきに伸び率が上がった気がします。
14回折ったときには、小学生の高学年くらいの高さまでになっています。
15回では2mを超え、人間の身長よりも高くなりました。実際に紙を折っていると、この時点で「どうやって次折るの？」となりそうです。
20回折ったときは、もう少しで100mへとどきそうですね。
スポンサーリンク
富士山より高く！
さらに折り進めます。30回まで行きましょう。
| 折った回数 | 紙の厚さ(m) |
|---|---|
| 21 | 167.77216 |
| 22 | 335.54432（東京タワー） |
| 23 | 671.08864（スカイツリー） |
| 24 | 1,342.17728 |
| 25 | 2,684.35456 |
| 26 | 5,368.70912（富士山を超えた） |
| 27 | 10,737.41824（飛行機の高度） |
| 28 | 21,474.83648 |
| 29 | 42,949.67296 |
| 30 | 85,899.34592 |
22回折ると335mとなり、ついに東京タワー(333m)を超えました。そして、さらにそこから1回おって23回折ると、次はスカイツリー(634m)を見下ろせる高さです。
26回でついに富士山を超えました。※富士山の標高は3,776m
27回折ったときには、10,737mであり、もうこの高さは想像がつかないですね。飛行機が飛んでいる高さくらいでしょうか。エベレスト山（8,848m）は余裕で超えています。
単位をmからkmへ変えた方がよさそうです。10,737mは約10kmですね。
ついに宇宙に突入！
では40回までおり進めましょう。ここからは単位がkmになっていることに注意してください。
| 折った回数 | 紙の厚さ(km) |
|---|---|
| 31 | 171.798 |
| 32 | 343.597 |
| 33 | 687.194（大気圏突破＝宇宙に到達） |
| 34 | 1,374.389 |
| 35 | 2,748.779 |
| 36 | 5,497.558 |
| 37 | 10,995.116 |
| 38 | 21,990.232 |
| 39 | 43,980.465（地球の外周よりの長い） |
| 40 | 87,960.930 |
33回目についに大気圏を突破！ついに、折り紙が宇宙空間へ到達したのです。折り紙を33回も折らないでくださいね。地球から出ちゃいます。
39回折ると、約44,000kmです。地球の外周が40,075kmですので、地球一周よりも長い折り紙の完成です。そのまま横に倒すと、折り紙に自分の頭を後ろから叩かれますよ。
40回目で87,960kmです。月までの距離が384,400kmですので、もう少しです。
スポンサーリンク
そして月へ
さらに、あと3回折りましょう。
| 折った回数 | 紙の厚さ(km) |
|---|---|
| 41 | 175,921.860 |
| 42 | 351,843.720 |
| 43 | 703,687.441 |
42回目で、約352,000kmです。月まで(384,400km)にあとわずか足りません。
そして、43回目についに月を超えました。
結論、”折り紙を42回折れば、ほぼ月までの高さになる”ということですね。
どうでしょうか？とっても少ない回数と感じませんか？
これなら、折れそうですよね！
ちなみに、太陽まで（149,600,000km）には、51回でした。
このように、どんどん倍にしていく計算というのは、人の予想よりもはるかに早く膨大な数になってしまうのです。
ここで示したように、自分が思っていることと、現実が全然一致しない現象のことを”パラドックス”といいます。
パラドックスは意外とたくさん存在し、人間の直感がいかにあてにならないかを認識されられます。興味がある人は以下の記事をチェックしてみてください。
https://analytics-notty.tech/interesting-paradox-of-math/
42回折ってみよう！
42回なんて余裕で折れそうですよね。42回折って、月へ行っちゃいましょう！
月は無理でも富士山くらいは行けるでしょ。
A4の紙で挑戦してみました。
結果は、7回まで折れましたが、8回目はどうやっても無理でした…
まっ、分かってたけどね。…でもこんなに折れないもんだとは…
数式で表現
折った回数と紙の高さを、数式で表現してみましょう。どのように考えればよいでしょうか？
紙の厚さは、ここでは\(0.08mm\)としました。これをはじめの高さ\(l_0\)とします。
1回折ると、2倍になりますから、高さ\(l\)は、
$$l = 2 \times l_0$$
となりますね。
2回折ると、さらにこれの2倍ですので、
\begin{align}
l &= 2 \times (2 \times l_0)\\
&= 2^2 \times l_0
\end{align}
です。
同じように、3回折ると、
\begin{align}
l &= 2 \times (2 \times (2 \times l_0))\\
&= 2^3 \times l_0
\end{align}
です。
さて、何かに気づきませんか？
紙を折るにつれて、どんどん\(2\)を掛けていきますが、その掛ける回数は紙折った回数となっています。
よって、\(n\)回折ったときの高さは、
$$l = 2^n \times l_0$$
と表現できます。
では、チェックのために、42回折った場合を上の数式から計算してみましょう。\(n\)に42を代入して計算してみてください。※計算には、電卓を使わないととても無理ですね。
$$l = 2^42 \times 0.00008 = 3,518,437,20.888 (m)$$
※\(l_0\)は0.08mmから単位を変えて、\(0.00008\)mとしている。
よって、351,843.720kmとなりました。
これは、前に示した表と一致しています。よって、この式で正しく高さを計算できていることが確認できました！
まとめ
- 人間の数学的な直観はあてにならない
- 折り紙を折った高さは次の通り
- 紙を23回折ると、スカイツリーに届く
- 富士山まで届かせるには26回折ればよい
- 33回目でついに地球の大気圏をぬけ宇宙に達する
- 月まで届くための回数は42回
- 太陽までは51回折る必要がある
- 実際にチャレンジしたら7回折るのが限界だった。