エラトステネスはどうやって地球の大きさを知ったのか – 2000年前とは思えぬ脅威の精度
今から約2000年前、古代ギリシャのエラトステネスは地球の大きさを知ることに成功しました。
その精度は、現在知られている正確な値と比べてわずかに1.7%の誤差しかないほど正確なものでした。
いったいどうやって地球の大きさを測ったのか。その方法を紹介します。
エラトステネスが地球を測った方法
紀元前240年(約2000年前)、ギリシャの天文学者エラトステネスは、地球の大きさをはじめて測量した人物として知られています。
その方法は、
二つの遠く離れた街にできる影の角度と街の距離の情報から地球の円周を求める
というものでした。
彼の推定した地球の精度は2000年前にも関わらず、脅威の精度で地球の大きさを計算できていました。
彼がどのようにして地球の大きさを計算したのかを詳しく見てみましょう!
スポンサーリンク
どうやって地球の大きさを求めたのか
井戸の影がヒントを与えた
エラトステネスは、エジプト北部の地中海沿岸のナイル川のほとりにあるアレクサンドリアの都市に住んでいました。
彼は毎年夏至(太陽が最も高く上がる日)の日に、エジプト南部のシエネの町の夏至が井戸の底に影がないことを知っていました。
つまり、毎年その日の正午に、太陽がシエネで頭上にあることを意味します。

また、エラトステネスは太陽がシエネより北にあるアレクサンドリアの夏至の正午は、太陽が真上にないことも知っていました。よって、アレクサンドリアの井戸では、影ができます。
シエネとアレクサンドリアで井戸の影のでき方が違うということは、地球が丸いということを証明しています。
なぜかというと、下の図を見てください。
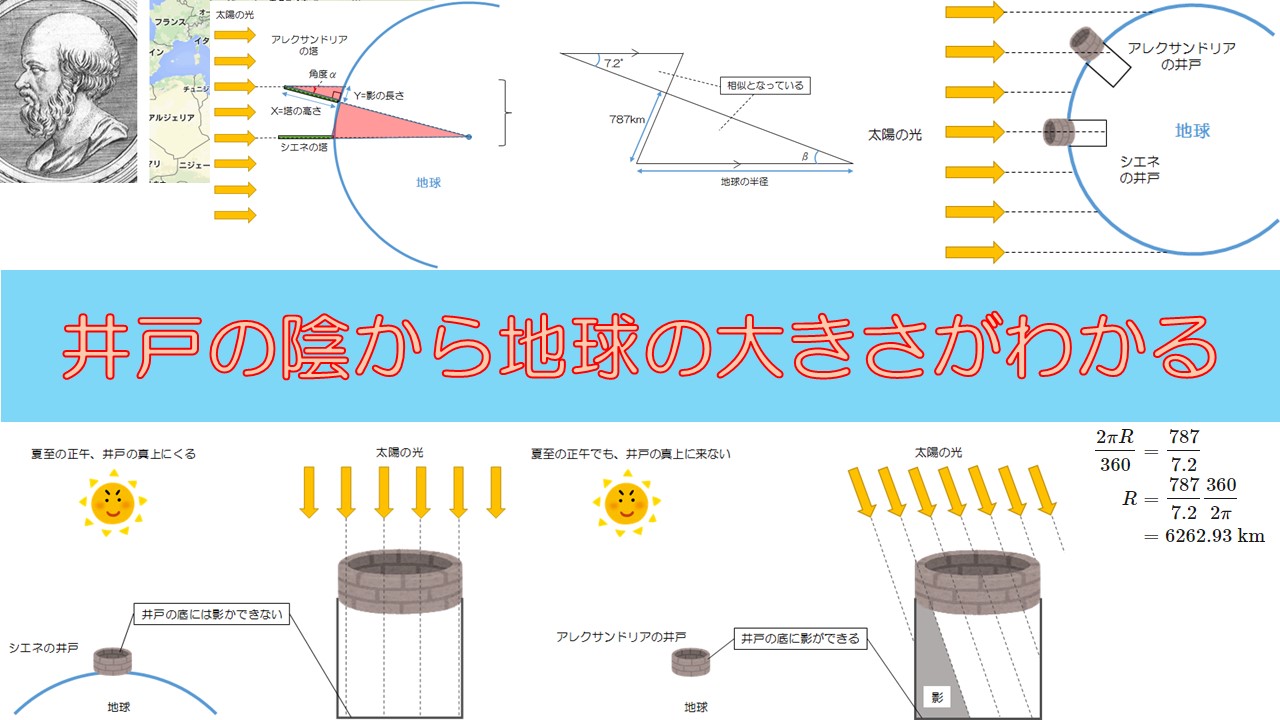
シエネの井戸の真上に太陽がきているとき、もっと緯度が高いところにあるアレクサンドリアの井戸では、影ができることがわかります。※本当はアレクサンドリアとシエネはこんなに緯度は変わらないのですが、わかりやすさのために極端に離して描いています。
影から角度を求める
このことが地球の大きさを調べるカギとなることに気づいたエラストテネスは、井戸の代わりに高い塔を建てて影を測りました。
エラトステネスは、塔の高さを知っていますし、影の長さもわかります。これより、上の図の角度\(\alpha\)がわかります(下の図参考)。
\(\alpha\)の角度は、7.2度でした。
また、エラトステネスは、アレクサンドリアとシエネの距離も測りました。その距離は787kmです。当時は、測量の技術は現代のような便利は道具はなかったため、アレクサンドリアとシエネまで歩いたときの歩数を数えて測量したと言われています。
三角形の相似に注目
\(\alpha\)と二つの塔の間の距離が分かったところで、以下の二つの三角形に注目してみましょう。
上の赤い二つの三角形を右に描きました。この二つの三角形は相似となっていることがわかりますね。
ということは、大きい三角形の角度\(\beta\)も同じ7.2度ですね。
これで必要な情報がそろいました。
地球の半径を\(R\)とすると、地球は丸く球の周りの長さは、
$$2 \pi R$$
ですので、360度が\(2 \pi R\)、7.2度で787kmとなり、
\begin{align}
\frac{2 \pi R}{360} & = \frac{787}{7.2} \\
R & = \frac{787}{7.2} \frac{360}{2 \pi} \\
& = 6262.93 \text{ km}
\end{align}
となります。よって、地球の半径は6263kmとなります。
エラトステネスはこうやって地球の大きさを求めたのです。
脅威の測定精度
ちなみに、正確な地球の半径は、6371kmです。その差は、
$$6371 – 6263 = 108\text{ km}$$
であり、わずか1.7%の誤差しかありません。
約2000前の測量技術を考えるとこの誤差の小ささは驚異的といっていいでしょう。
その他のエラトステネス功績
エラトステネスが残した功績としてもう一つ有名なものがあります。
それは、”エラトステネスのふるい”と呼ばれる素数を発見する方法です。
素数とは、自分自身の数と1以外で割ることができない数です。
2から順に素数を見つけていくとき、素数が現れるのに規則性はありません。そのため、いま考えている数字に対して割れないことを一つ一つ確かめていく必要があります。
しかし、”エラトステネスのふるい”を使うことで、比較的簡単に素数を見つけていくことができるのです。
ちなみに、素数が現れるのに規則性がないという性質は私たちの生活に非常に役に立っているのです。それは、メールなどを送信するときの暗号化に対して、この性質が利用されています。
興味のある方は以下の記事をご覧ください。
スポンサーリンク
まとめ
- エラトステネスは二つの離れた町の井戸にできる影が違うことから地球の大きさを測ることができると気づいた
- 高い塔を立て地面にできる影の長さを求めるとこで太陽の光と塔の角度を求めた
- その角度と二つの町の距離の情報を使って、地球の半径を求めることに成功した
- 測定された値は誤差が1.7%しかなく、非常に高精度で測定されたものであった





























ディスカッション
コメント一覧
エラトステネスの地球の円周を求める問題です。日本の伊能忠敬も地図を作る本当の理由は、円周を求めたかったからだと聞きました。少年のような好奇心に心打たれました。ところで、私は分数の割算の逆数も最近理解できるようになった算数入門者です。ですので、相似をどうしても求めることができません。
できれば、易しく解説してください。対頂角はわかるのですが、辺の比がわからないのに、どうして相似になるのか、わかりません。すみません。
エラトステネスの地球の円周を求める問題です。相似がどうしてわかるのかが、
わかりません。できれば、算数初心者でもわかるようにぜひ、解説してくだされば幸いです。対頂角はわかったのですが、辺の比がわからないのに、相似形になるのが私には導けませんでした。すみません。貴重な時間をとらせてしまいますね。よろしくお願いします。
私も三角形が相似だからβも7.2度になるというのはあまりピンときませんでした。
対頂角の2つの対辺は図で明示されているように平行であるので、平行線の錯覚は等しいという性質から、対頂角ではない2つの角もそれぞれ等しいことが分かります。
2つの三角形が相似であることの証明も上記でできていますが、そもそもβが7.2度であることを証明するのが目的なので、相似の証明過程でそれが必要なのはおかしいなと。私が不勉強なだけかもしれませんが。
私も三角形が相似だからβも7.2度になるというのはあまりピンときませんでした。
対頂角の2つの対辺は図で明示されているように平行であるので、平行線の錯覚は等しいという性質から、対頂角ではない2つの角もそれぞれ等しいことが分かります。
2つの三角形が相似であることの証明も上記でできていますが、そもそもβが7.2度であることを証明するのが目的なので、相似の証明過程でそれが必要なのはおかしいなと。私が不勉強なだけかもしれませんが。
ピンバック & トラックバック一覧
[…] やっぱ有識者は違うわ https://analytics-notty.tech/eratosthenes-calculation-of-earth-size/ […]
[…] 画像引用:https://analytics-notty.tech/eratosthenes-calculation-of-earth-size/ […]
[…] 画像引用:https://analytics-notty.tech/eratosthenes-calculation-of-earth-size/ […]