【高校数学(因数分解)】4乗が登場する式の因数分解 – 置き換えをして見慣れた形に直して解こう

- 4次式の因数分解の解き方がわからない
- 4乗が登場する因数分解のパターンを知りたい
- ”置き換え”って何をすればいいのかわからない
- 計算数が多すぎるから嫌だ
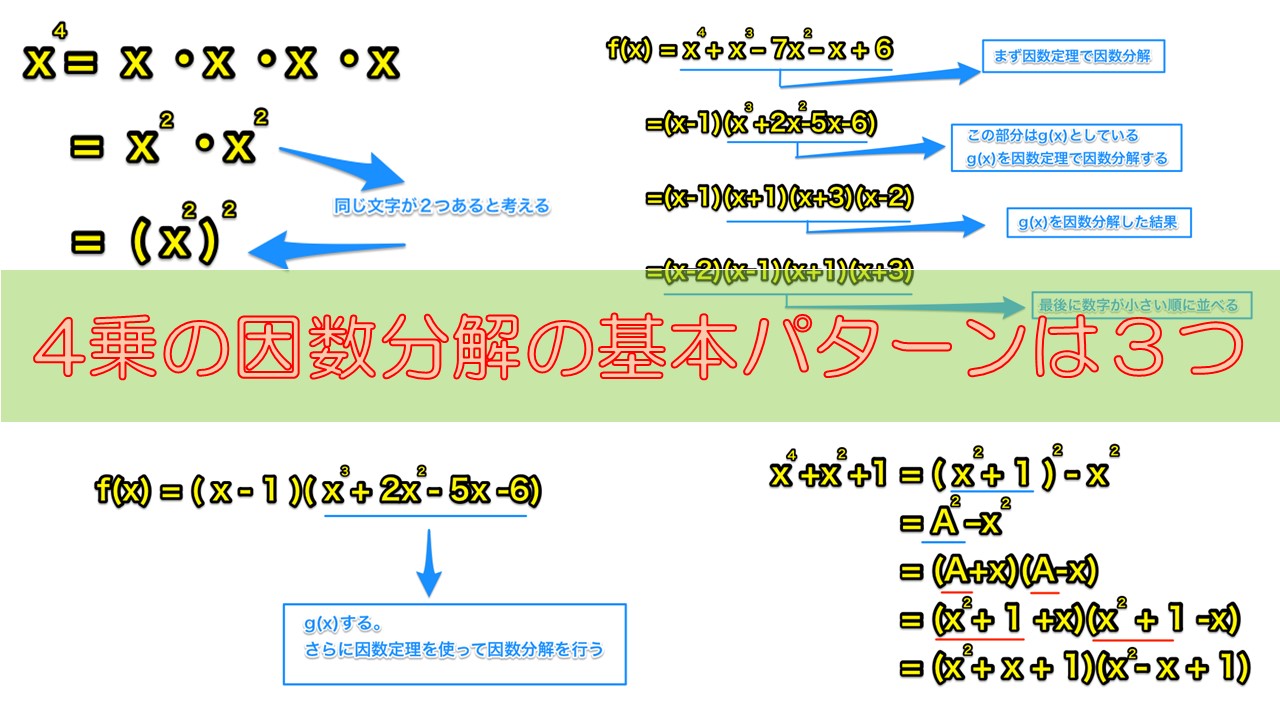
4乗が登場する因数分解には、大きく分けて3つのパターンがあります。
この3つをマスターすると、あなたの因数分解能力はかなりのレベルに達するでしょう。
少し長い解説になりますが、一日少しずつでもいいので徐々に進めていってくださいね。
4乗が登場する因数分解の基本は3つ
4次式の基本的な因数分解の方法は”置き換え”を行うことです。
まずは、この「置き換えをして因数分解をする方法」を学びます。
次に、置き換えをする前に、少し式変形をしておかなければならない場合があります。
ここに気づくようになると、他の人に一歩差をつけることができます。
最後は、置き換えを使わない場合です。
その場合、因数定理を使い因数分解をする必要があります。
しかし、因数定理が理解できている人でも、計算数が多くなるのでミスをしないように反復して解く練習をすることが必要です。
以上、3つが4乗の因数分解の基本となります。
では、一つずつ見ていきましょう。
スポンサーリンク
4乗の式の因数分解に必要な”置き換え”
まず、
$$x^2=x \times x$$
であることは理解できていますか?
同じ数字、文字を2回掛け算することを2乗(にじょう)といって\(x^2\)と表現します。
同じように、3回掛け算するときは、
$$x^3=x \times x \times x$$
と書きます。
次に、
$$x^4 = x \times x \times x \times x$$
ですが、これをよく見てみましょう。
$$x^2=x \times x$$
なので、
\(x^4\)は次のように式変形できます。
\begin{align}
x^4 &= x \times x \times x \times x \\
&= (x \times x) \times (x \times x) \\
&= x^2 \times x^2 \\
\end{align}
同じ数字、文字を掛け算することで2乗になるのでしたね。
上の式は\(x^2\)が2つあるので、さらに、
\begin{align}
x^4 &= x^2 \times x^2 \\
&= (x^2)^2
\end{align}
と表すことができます。( )をつけるのは\(2\)乗が2つあると間違いやすく、見づらくなるからです。
つまり、\(x^4\)は、
$$x^4=(x^2)^2$$
と表せます。
これで4乗の因数分解を解く準備はできました。
しかし、\(2\)乗が2つあるという表現(\(x^2)^2\)は少し複雑で、計算の途中式がわかりにくくなることがあります。
そのため、別の文字に置き換える方法も覚えておきましょう。
別の文字に置き換えるというのは、\(x^2\)を一つの文字に置き換えるということです。
置き換える文字はなんでも良いのですが、ここでは大文字の\(A\)を使いましょう。
※テストなどで実際に置き換えを行うときは、自分の好みの置き換え文字を使って構いません。他に登場する文字とかぶらない文字を選ぶようにしましょう。
\(A=x^2\)と置き換えると、\(x^4\)は、
\begin{align}
x^4 &= (x^2)^2 \\
&= A^2
\end{align}
と表せます。
これが重要なポイントです。
図でまとめておきましょう。
これでとてもシンプルに式を表現できるようになりましたね。
ここまでは大丈夫でしょうか?
置き換えの意味を理解できたら、次に進みましょう。
次はいよいよ問題を解いていきます。
置き換えを使った因数分解の問題(基本)
置き換えを使う因数分解の問題は、おおよそ式の形に決まりがあります。
基本的に、
置き換えを行うときの式には、\(4\)乗と\(2\)乗のみ
が出てきます。
以下の図の形を覚えましょう。
この形が出てきたら、「置き換えだ!」と考えてください。
後で説明しますが、\(x^3\)や\(x\)の項があると、置き換えによる因数分解法は使えないです。
実際に問題を解いていきましょう。
\(x^4+3x^2+2\)を因数分解せよ。
式を見てみると4乗と2乗のみが出てきていますね。
よって、置き換えを利用します。
テストで置き換えを行う時は、必ず回答の最初に自分で、
「\(A=x^2\)とする」
と書きましょう。
いきなり\(A\)を使ってしまうと、回答を見ている先生などは、なぜいきなり\(A\)が出てきたのかわかりませんからね。
\(A=x^2\)と置き換えたので式を変形していきます。
\begin{align}
x^4+3x^2+2 &= (x^2)^2+3x^2+2 \\
&= A^2 + 3A +2
\end{align}
どうですか?
置き換えをしてあげると二次方程式に変形できましたね。
これで、見慣れた形の式になったと思います。因数分解も簡単ですね。
あとは文字\(A\)のまま因数分解していきます。
$$A^2+3A+2 = (A+2)(A+1)$$
と因数分解できました。
しかし、このままで終わってしまってはいけません。
自分で\(A=x^2\)と決めたのですから、\(A\)を使ったままではダメです。
問題に沿って、\(x^2\)に直しましょう。
\begin{align}
A^2+3A+2 &= (A+2)(A+1) \\
&= (x^2+2)(x^2+1)
\end{align}
ここまで直して正式な答えとなります。
図でまとめましょう。
4乗の因数分解の問題(二回、因数分解できるパターン)
もう一問似たような問題を解きましょう。
これはまだ上のパターンと同じ扱いです。
\(x^4-2x^2-8\)を因数分解せよ。
例題①とほぼ同じような問題ですね。
まず、\(A=x^2\)とします。
\begin{align}
x^4-2x^2-8 &= (x^2)^2-2x^2-8 \\
&= A^2-2A-8
\end{align}
そして、文字\(A\)のまま因数分解していきます。
$$A^2-2A-8 = (A-4)(A+2)$$
自分で\(A=x^2\)と決めたので\(x^2\)に直します。
\begin{align}
A^2-2A-8 &= (A-4)(A+2) \\
&= (x^2 – 4)(x^2 + 2)
\end{align}
以上で終了……でいいのでしょうか?
テストでは、もしまだ因数分解できるのであれば、できるところまで因数分解しなくてはいけません。
何かに気づきましたか?
そうです!\((x^2–4)\)はまだ因数分解できますね!
$$(x^2–4)=(x-2)(x+2)$$
となります。
よって、正しい回答はさらに因数分解を進めて、
\begin{align}
(x^2–4)(x^2+2) = (x – 2)(x + 2)(x^2 + 2)
\end{align}
となります。
初めから式を書くと以下のようになります。
\begin{align}
& \text{はじめに(\(A=x^2\)とすることを書いておく)} \\
x^4-2x^2-8 &= (x^2)^2-2x^2-8 \\
&= A^2-2A-8 \\
&= (A-4)(A+2) \\
&= (x^2–4)(x^2+2) \\
&= (x-2)(x+2)(x^2+2)
\end{align}
ここで言いたかったことは、
「一度、因数分解ができても安心するな!まだできるかもしれないと思え!」
ということです。
特に4乗の因数分解の問題は、この2回因数分解できるパターンはよく出題されます。
スポンサーリンク
少し特殊な4乗の因数分解
次です。
少し頭を使うので、落ち着いてから取り組んでください。
では、例題を見てみましょう。
\(x^4+x^2+1\)を因数分解せよ。
例題①,②と同じような問題に見えますね。
「楽勝!」と思いますか?
では解いてみます。
\(A=x^2\)として、
\begin{align}
x^4+x^2+1 = A^2+A+1
\end{align}
ですね。
ここまでは同じです。
しかし、このあと因数分解ができないのに気づきますか?
解の公式に当てはめる方法(「解の公式を使ってルートが登場する因数分解を解けるようになろう」を参照)であれば、因数分解を先へ進めることができますが、すごく複雑になりそうです。
このような場合は少しだけ工夫が必要です。
それは、
$$x^4+x^2+1 = (x^2+1)^2-x^2$$
と式変形をするのです。
「どうやってそんな変形したの?」という人は慣れるしかありませんが、逆に
$$(x^2+1)^2-x^2$$
を展開してみると理解できます。
\begin{align}
(x^2+1)^2-x^2 &= x^4+2x^2+1–x^2 \\
&= x^4 +x^2 +1
\end{align}
となり、確かに同じ式になっているようですね。
図でも確認してみましょう。
なぜこのような式変形をするのか、その理由を説明しましょう。
\(x^2+1\)を\(A\)と置き換えると、\(A^2–x^2\)になっていることがわかるでしょうか?
$$(x^2+1)^2-x^2 = A^2–x^2$$
よって、
\begin{align}
x^4+x^2+1 &= (x^2+1)^2-x^2 \\
&= A^2–x^2 \\
&= (A+x)(A-x) \\
&= (x^2+1+x)(x^2+1–x) \\
&= (x^2 +x +1)(x^2 –x +1)
\end{align}
と因数分解することができるんです。
下の図の線を引いたところが対応している箇所です。
一つずつ式を進めて、確認してみてください。
例題①,②に比べて、一度式変形をしないと問題が解けないところがポイントです。
「4乗が出てきてるから\(A=x^2\)と置いてみたけど、因数分解できそうにないなぁ」
というときには、こちらの可能性を検討してみましょう。
ここまで例題①,②,③と紹介してきましたが、どうだったでしょうか?理解できましたか?
特に例題③のような問題は何回も繰り返し練習しないと、すぐに思いつくことができないので反復練習が必要ですね。
これで置き換えを利用した因数分解は終了です。
次は、4乗が登場する式を因数分解するため、因数定理を使う方法を紹介します。
これが最後ですので、ファイトです!
因数定理を使った4次式の因数分解
さて、では最後に因数定理を使った4次式の因数分解をやっていきましょう。
この因数分解は割り算を使った因数分解の一種です。
「割り算を使った因数分解を知らないよ」という人は、以下のページをまずは読んでみてください。
また、因数定理がわからないという方はこの記事を見ましょう
[ブログカード]
では、例題にチャレンジしましょう。
\(f(x) = x^4 + x^3 – 7x^2 – x + 6\)を因数分解せよ。
この問題をぱっ!と見て今までの問題との違いが分かりますか?
そうです。今までは\(x^4\)と\(x^2\)しか問題式に登場していませんでした。
しかし、今回の問題式は\(x^3\)や\(x\)も登場しています。
このような場合、これまでのように\(A=x^2\)とおいて式を変形する方法ではうまくいかないのです。
なので、基本的には、
\(x^3\)や\(x\)の項が式にあれば、\(A=x^2\)の置き換えは使えない
と覚えておきましょう。
では、どうすればよいのか?
まずは、因数定理によって\(f(x)=0\)となる\(x\)を探しましょう。
つまり、問題式の\(x\)にどのような数を入れれば、\(0\)になるかを探すんです。
この式では\(x\)に\(1\)を代入してみましょう(\(1\)以外の数字が見つかった人はその数字でもOKです)。
\begin{align}
f(1) &= 1^4+1^3–7 \cdot 1^2–1+6 \\
&= 1+1-7-1+6 \\
&= 0
\end{align}
となるので、因数定理より\(f(x)\)は\((x-1)\)で割り切れることがわかります。
では、\(x-1\)で割り算をしましょう。
上の式のように割り切れるので、
\begin{align}
f(x) &= x^4+x^3–7x^2–x+6 \\
&= (x-1)(x^3 +2x^2-5x-6)
\end{align}
となります。
ちょっとだけ、因数分解したっぽい形になりましたね。
次に、\(x^3 +2x^2-5x-6\)を因数分解していきます。
これも因数定理を使っていきます。
\(g(x)=x^3+2x^2-5x-6\)としましょう。
\(g(x)=0\)になる\(x\)を探すと\(x=-1\)のとき、
\begin{align}
g(-1) &= (-1)^3+2(-1)^2-5(-1)-6 \\
&= -1+2+5-6 \\
&= 0
\end{align}
となるので、
\(g(x)\)は\((x+1)\)で割り切ることができます。
割り算をしていきましょう。
図のように割り切れるので、
\begin{align}
g(x) = x^3+2x^2-5x-6 \\
&= (x+1)(x^2+x-6) \\
&=(x+1)(x+3)(x-2)
\end{align}
となります。上の式で、2式目から3式目にいくとき、さらに因数分解していることに注意です。
この結果を元の式\(f(x)\)に代入してみると、
\begin{align}
f(x) &= (x-1) g(x) \\
&=(x-1)(x^3+2x^2-5x-6) \\
&=(x-1)(x+1)(x+3)(x-2) \\
&=(x-2)(x-1)(x+1)(x+3)
\end{align}
となり、これが因数分解の答えです。
少し数字が多くなったので、図の解説でまとめてみましょう。
最後は、数字が小さい順に並べ替えています。
並べ替えると見やすくなりますので、めんどくさがらずに並べ替えて終わりましょう。
例題④では因数定理を使い、2回もメンドウな整式の割り算を行いました。
同じことを繰り返すだけなのですが、計算が長いのでミスが起こりやすいです。
テストで解くときは気をつけましょうね。
以上で基本的な4次式の因数分解は終了です。
特に例題③,④が難しいですが、頻出問題なので重点的に練習しておきましょう。
スポンサーリンク
まとめ
4乗が登場する因数分解の解き方を説明してきました。
基本的な4乗の因数分解は、上で紹介した3種類なので、これだけマスターしておけばとりあえずはオッケーです。
では、以下に重要なポイントをまとめて終わります。
4乗が登場する因数分解は、
- 置き換えをする
- 式変形をしてから置き換えをする
- 因数定理を使い、2回割り算をして因数分解する
が基本のパターンです。
特に、
- 式変形をしてから置き換えをする
- 因数定理を使い、2回割り算をして因数分解する
の二つは繰り返し理解し、練習しないと身につきませんので問題をたくさん解いておきましょう。


























ディスカッション
コメント一覧
途中の計算が間違ってましたが、解く手順はあってたので無事に理解することが出来ました!間違った計算がなければもっとサラッと自分の中に入ったと思ってます
Hello.
雀の涙の年金ですが、時間はたっぷりあり惚け防止と暇つぶしに初心に戻り頑張っております。
分かりやすかったです!これからも利用させて頂きます!
コメントありがとうございます。励みになります。
何かこれを説明して欲しいというテーマはありますか?
x⁴-x³-7x²-x+6
=x⁴+x³-x²-x-6x²+6
=x²(x²-1)+x(x²-1)-6(x²-1)
=(x²-1)(x²+x-6)
=(x+1)(x-1)(x+3)(x-2)