【高校数学（因数分解）】解の公式を使ってルートが登場する因数分解を解けるようになろう
- 基本的な因数分解はできるようになったけど、ルート（\(\sqrt{\text{ }}\)）を使った因数分解ができない
- 解の公式を使った因数分解の仕方がわからない
ルート（\(\sqrt{\text{ }}\)）が登場する因数分解は、解の公式を使うことで解くことができます。
「どう頑張っても通常の方法では因数分解できないじゃない！」
というときに解の公式を使いましょう。
解の公式は次のようなものでした。
$$x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$$
解の公式は二次方程式を解くための便利な公式でしたね。
これを使えば、因数分解だってできるようになるんです。
その方法を丁寧に解説していきますので、じっくりと理解しながら進んでくださいね。
はじめに
ここでは、ルートが登場する因数分解を見ていきます。
ここから先を読み進めるための基礎知識として、基本的な因数分解はマスターしていることが必要です。
まだ、因数分解に慣れていないのならば、基本的な因数分解をしっかりと学んでからルートが登場する因数分解の勉強をしましょう！
以下のリンクのページを理解すれば、オッケーですよ。
https://analytics-notty.tech/factorization-of-quadratic-expressions/
ルートの因数分解は、あなたが解の公式を使えるのであれば、計算自体は難しくはありません。
基本的には二次方程式を解の公式を使って、因数分解していくからです。
しかし、因数分解のために二次方程式を解く理由がわからないと、なぜ解の公式を使って二次方程式を解く必要があるのかわからなくなります。
その辺りに注意して読み進めてください。
スポンサーリンク
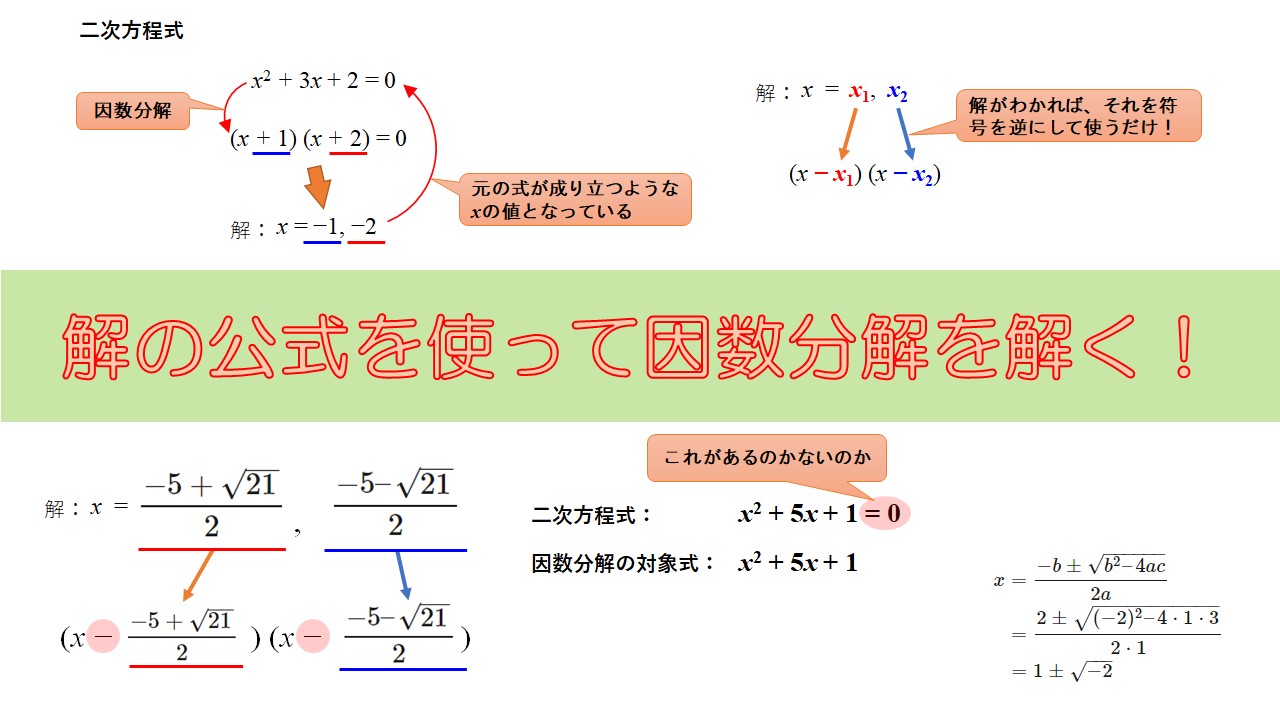
因数分解と二次方程式の関係
まずは、因数分解と二次方程式の関係を考えてみましょう。
難しそうに聞こえますが丁寧に説明していきますので大丈夫です。
まず簡単な因数分解を解いてみます。
\(x^2 + 3x +2\)を因数分解せよ。
これはルートなどは使わない簡単な因数分解ですね。
答えは、
$$x^2 + 3x +2 = (x+1)(x+2)$$
ですね。
では次に同じ式ですが、二次方程式を解いて見ましょう
\(x^2 + 3x +2=0\)を解け。
右辺に\(=0\)が付いていますね。ここが違いです。
この式を解くためには、まず左辺を因数分解する必要がありますね。
すると、
$$(x+1)(x+2) = 0$$
となり、答えは、
$$x=-1, -2$$
です。
このように、
「方程式\(x^2 + 3x +2\)を解いたら、解が\(x=-1, -2\)になった」
という意味は、
\(x^2 + 3x +2=0\)の式に\(x=-1, -2\)を代入するとちゃんと\(0\)になるよね！
ということなんです。
実際に、問題の式に答えの二つの\(x\)の値を代入して確かめてみましょう。
まず、\(x=-1\)を問題の式に代入すると、
\begin{align}
x^2 + 3x +2 &= (-1)^2 + 3 (-1) +2 \\
&= 1 – 3 + 2 \\
&= 0
\end{align}
です。
また、\(x=-2\)を代入すると、
\begin{align}
x^2 + 3x +2 &= (-2)^2 + 3 (-2) +2 \\
&= 4 – 6 + 2 \\
&= 0
\end{align}
です。
ちゃんと\(0\)になっていますね。
このように、
因数分解して二次方程式の解を見つけるというのは、問題式が成り立つ\(x\)の値を求める
ということなのです。
さて、二次方程式と因数分解の関係をまとめておきましょう。
次の図を見ておさらいしてから、先へ進んでください。
ここで、因数分解した式の赤と青の線と、解の値に注目です。
これは、符号が逆になっている値ということがわかりますね。
このことは、非常に大事なので覚えておいてください。
因数分解するためには解がわかればいい！
上の図から言えることを考えてみましょう。
上の例では簡単に因数分解できる式（\(x^2+3x+2\)）でした。
しかし、これが簡単には因数分解できない式だったらどうでしょうか？
例えば、
$$x^2 + 5x +1$$
は、これまでの方法（解の公式を使わない方法）ではどうやっても因数分解できないでしょう。
ただ、これを二次方程式、
$$x^2 + 5x +1 = 0$$
にして（\(=0\)をくっつける）、解がわかった状態になったとします。
下の図のようなイメージです。
するとどうでしょうか？
もう一度、前の図を見直してみましょう。
上の図で、今度は解の方に注目します。
解と因数分解に使われる数は、符号が違うだけでしたね。
ということは、解がわかれば因数分解した式もわかってしまうというわけです。
解がわかれば、上の図のようにその符号を逆にして（ ）の中に入れればいいのです。
そして、その解は解の公式を使って求めればいいでしょう。
解の公式は、二次方程式であればどんなものも解けてしまいますから、どんな因数分解でもできるというわけです。
では、解き方をまとめておきましょう。
- 「この式は因数分解できないぞ！」と思ったら、「\(=0\)」を付け足して二次方程式にしよう
- その二次方程式の解を”解の公式”を使って求めよう
- 最後に、解の符号を逆にして\((x + ?)(x + ?)\)の\(?\)の部分に入れてやればオッケー！
解き方の流れが分かったところで、次からは実際の問題を解いていきましょう。
スポンサーリンク
解の公式を使ってルートが登場する因数分解を解く
ルートが登場する因数分解
\(x^2 – 4x +2\)を因数分解せよ。
この問題を見たときに、
「掛け算をして\(2\)、足して-4になる数字の組み合わせなんてない！だから因数分解できないじゃないか！」
と思ったとしたらすばらしいです！
その通りなので、解の公式を使った方法を使って解きましょう。
通常の因数分解ができないときには、まず二次方程式にするのでしたね。
$$x^2 – 4x +2 = 0$$
次に、解の公式を使ってこの方程式を解きましょう。
\begin{align}
x &= \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \\
&= \frac{-(-4) \pm \sqrt{(-4)^2 – 4 \cdot 1 \cdot 2}}{2 \cdot 1} \\
&= 2 \pm \sqrt{2}
\end{align}
です。
答えの、
$$x = 2 \pm \sqrt{2}$$
というのは、答えが、
$$x = 2 + \sqrt{2}, \quad 2 – \sqrt{2}$$
の2通りあるよ！ということです。
では、ここで以下の図をもう一度確認です。
でしたね。
いまの問題の場合、\(x_1, x_2\)は、
\begin{align}
x_1 &= 2 + \sqrt{2} \\
x_2 &= 2 – \sqrt{2}
\end{align}
です。
よって、下の図のように（ ）の中に入れてやればいいですね。
後は、これを計算して内側の括弧をとってあげれば完了です。
\begin{align}
(x-(2+\sqrt{2}))(x-(2-\sqrt{2})) = (x-2-\sqrt{2})(x-2+\sqrt{2})
\end{align}
よって、\(x^2 – 4x +2\)を因数分解すると、
$$x^2 – 4x +2 = (x-2-\sqrt{2})(x-2+\sqrt{2})$$
となり、これが答えです。
符号が変わるところを間違えないように気をつけましょう！
どうですか？
では、次はもう少しレベルをあげますよ！
分数が混じったルートが登場する因数分解
上と同じような問題を解いて見ましょう。
\(x^2+5x+1\)を因数分解せよ。
問題①と同じように、
「因数分解できない！」
となるので、下の式のように二次方程式を作って（\(=0\)をくっ付けて）から、解の公式を使ってを解きましょう。
$$x^2+5x +1=0$$
この二次方程式を解の公式で解くと、
\begin{align}
x &= \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \\
&= \frac{-5 \pm \sqrt{5^2 – 4 \cdot 1 \cdot 1}}{2 \cdot 1} \\
&= \frac{-5 \pm \sqrt{21}}{2}
\end{align}
となります。
では、しつこいですが下の図をもう一度確認です。
いまの問題の場合、\(x_1, x_2\)は、
\begin{align}
x_1 &= \frac{-5 + \sqrt{21}}{2} \\
x_2 &= \frac{-5 – \sqrt{21}}{2}
\end{align}
です。
よって、下の図のように（ ）の中に入れてやればいいですね。
※符号に注意です。
この問題のように、解に分数が入ってくると、余計にごちゃごちゃしてしまい、嫌になりますよね。
でもやってる作業は一緒なので落ち着いて一つ一つ丁寧に進めていけば確実に解けます。
二次方程式を解いた答えと、因数分解の（ ）の中に入る数は符号を変えた数字ですが、分数なので分子の符号を変えることに意識しましょう。
つまり、最終的な答えは以下のような計算式となります。
\begin{align}
\left( x-\frac{-5 + \sqrt{21}}{2} \right)\left( x-\frac{-5 – \sqrt{21}}{2} \right) = \left( x + \frac{5 – \sqrt{21}}{2} \right)\left( x + \frac{5 + \sqrt{21}}{2} \right)
\end{align}
よって、\(x^2+5x+1\)を因数分解すると、
$$x^2+5x+1 = \left( x-\frac{5 – \sqrt{21}}{2} \right)\left( x-\frac{5 + \sqrt{21}}{2} \right)$$
となります。
ここまで出来ましたか？
答えにルートが出てきますが、ビビらずに計算できれば必ず解けます。
以上で、解の公式を使った因数分解のやり方は終了です。
…終了なんですが、最後に一つだけ覚えておいてほしいことがあるのでもう少しだけ頑張りましょう！
もうすぐです！
解の公式を使っても解けない因数分解
ここまで学ぶと、
「これで、全ての2次式は因数分解できる！」
と思うかもしれません。
それはその通りであり、全部できることに間違いはないのですが、正確にいうと、それは虚数\(i\)という数を学んでからになります。
虚数は後で学ぶのでここでは後回しにしましょう。
「ここでは、今の知識では因数分解できない式もある！」
覚えておきましょう。
では、どんなときに因数分解ができないのか？
簡単に言うと、ルートの中の数字がマイナスのときです。
実際に次の問題を解いてみましょう。
\(x^2-2x+3\)を因数分解せよ。
解の公式を使わないと出来ない因数分解なので、2次方程式として問題を解きましょう。
$$x^2-2x+3 = 0$$
解の公式を使って計算をすると、
\begin{align}
x &= \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \\
&= \frac{2 \pm \sqrt{(-2)^2 – 4 \cdot 1 \cdot 3}}{2 \cdot 1} \\
&= 1 \pm \sqrt{-2}
\end{align}
よって、
\begin{align}
x_1 &= 1 + \sqrt{-2} \\
x_2 &= 1 – \sqrt{-2}
\end{align}
という答えになります。
この時点で、もう因数分解できません。
見てわかるようにルートの中の数字は\(-2\)です。
今、学んでいる範囲ではルートの中にマイナスがあるのはルール違反です。（あくまで学校で因数分解を学ぶときの期間内ではです）
つまり現時点で、こんな問題は出題されないということになります。
できませんからね！安心してください。
ただし、「\(x^2-3x+3=0\)を解け」というような二次方程式の問題が出題された場合、解なしという答えになるので気をつけてください。
因数分解することと、方程式を解くというのは全くの別問題です。
因数分解は方程式を解くための道具として扱いましょう。
因数分解か二次方程式かの見分けは\(=0\)があるかないかで見極めれます。
以上で、ルートが登場する解の公式をつかった因数分解は終了です。
お疲れ様でした。
スポンサーリンク
最後に復習しよう
解の公式を使ったルートが登場する因数分解の解き方を説明してきました。
二次方程式を解の公式で解くことで、通常の方法ではできない因数分解もできるようになることがわかったでしょう。
では、以下に重要なポイントをまとめて終わります。
簡単にいうと、解の公式で求めた結果の符号を変え、\((x – x_1)(x – x_2)\)に入れるだけです。
符号の間違いに気をつけましょう！
ただし、因数分解と二次方程式の関係をしっかり理解しておきましょう。
このページの前半で説明した内容ですね。
分からないところがあれば、気軽にコメントくださいね。