【高校数学(因数分解)】複素数が登場する因数分解の方法

- 複素数が出てきたときの因数分解の方法を知りたい
- 複素数がわからないから嫌いだ!
- 因数分解できないと教わったのに、複素数を学ぶと因数分解できるようになるのはなぜ?
まだ複素数といういうものを習っていなかったときは、因数分解で「ルートの中が負になった場合、因数分解はできない」と教わってきたはずです。
本サイトの因数分解の解き方を紹介したページでも、ルートの中が負になったときは、「解なし」とすることと説明してきました↓
しかし、複素数を学ぶと、ルートの中が負になっても因数分解できるようになります。
※ただし、このページは複素数についてしっかり理解したい!という人向けではありません。あくまで、因数分解をするときに複素数をどう使っていくかということに説明の重きを置いています。
複素数の概念をさらっと知っておく
複素数というものは、昔の人が、
- もっと色々な計算をしたいけど、いままでの数学の概念だけでは計算を先へ進めることができない
- 複素数という数字を作ったら、今まで不可能だった計算ができるようになった
- でも、複素数は現実には存在しない数字だから虚数(きょすう)という名前にしよう!
(※”虚”とは、実態がないことを指す。)
と考えた不思議な数字です。
すごくざっくりですが、とりあえずはそんな理解で大丈夫です。
複素数をもっとちゃんと理解するとなると、色々な知識が必要になります。
なので、問題を解けるようにする!という観点(つまりはテストでいい点をとるという観点)では、理解に時間をかけずに、まずは使いこなせるようになることを優先しましょう!
以下では複素数について簡潔に説明しますが、理解できなくても「そういうものだ」という程度の理解で先へ進んでください。
スポンサーリンク
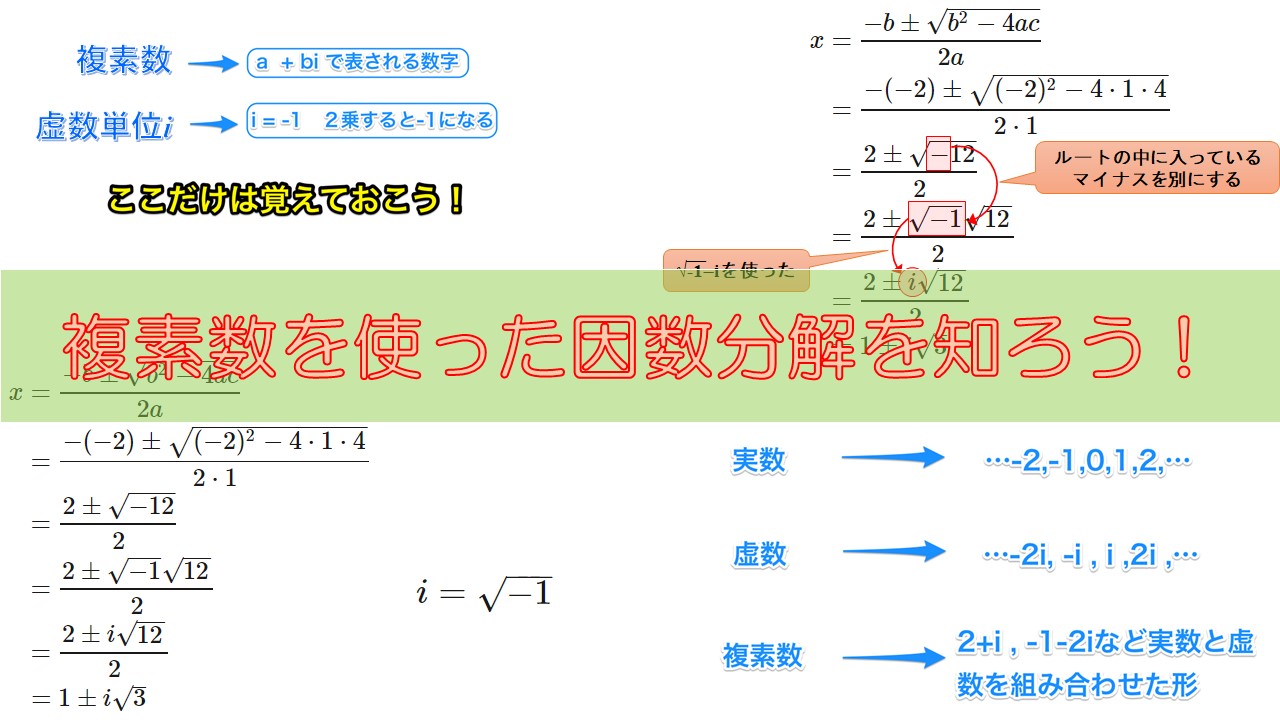
複素数の表し方
複素数とは実数と虚数を組み合わせたものです。
実数と虚数の違いは以下の図に示すように、\(i\)がついているかいないかです。
\(i\)が何かというのはまだ分からなくても大丈夫です。
一般的に以下のような形で表しています。

実数は今まで皆さんが習ってきた数字と考えてさい。
上の画像では、整数しか書いてありませんが、分数(\(\frac{3}{5}\))や小数(\(3.14\))、ルート(\(\sqrt{3}\))なども実数です。
虚数は実数に\(i\)をつけた数字と考えれば大丈夫です。
この\(i\)のことを虚数単位と呼びます。
そして、実数と虚数を組み合わせた数字(\(a + bi\))が複素数と呼ばれます。
虚数とは
複素数ははじめは慣れないでしょう。
しかし、問題を解くに連れて徐々に慣れていきます。
複素数でポイントになるのは虚数単位\(i\)です。
虚数単位\(i\)とは一言でいうと、
\(2\)乗すると\(-1\)になる数
です。
つまり、
$$i^2 = -1$$
が成り立つということです。
ということは、少し式変形をして、
$$i = \sqrt{-1}$$
も成り立ちますね。
この式が複素数の因数分解には非常に重要です。
なぜ\(i\)は文字なのに、数字として扱われるのでしょうか?
ここで考えて欲しいのは、皆さんは今まで学習してきた中で、
「\(2\)乗してマイナスになる数はないですよ」
と習ってきたということです。
しかし、より様々な計算をするためには、\(2\)乗してマイナスになる数がないと不便であると感じた数学者がいました。
「だったら勝手に作ってしまおう!でも今まで使ってきた数字では表現できないから、文字で表そう!」
それが虚数\(i\)です。
数字では表せないから、しかたなく文字にしたんですね。
要するに、日常生活には存在しないのに、数学の世界ではあたかも存在するように作ってしまったからイメージが難しいのです。
なので、ここでは\(i\)をイメージしようなんて考えないでください。
機械のように、
$$i^2 = -1$$
もしくは、
$$i = \sqrt{-1}$$
と覚えておけば大丈夫です。
スポンサーリンク
なぜ虚数を使うとルートの中が負になっても因数分解できるの?
今まではルートの中にマイナスが入っているのはダメ、もしくは「解なし」と習っていました。
それは、\(2\)乗すると負になる数を学習してなかったからです。
例えば、
\(\sqrt{-2}\)という数字は\(2\)乗すると\(-2\)になりますよね。
これを定義してしまうと(許してしまうと)、\(2\)乗すると負になる数が存在してしまいます。
学習した内容と矛盾してしまうので、今まではルール違反としていました。
しかし、虚数を習ったいま、もうルール違反とはなりません。
それは、
$$i = \sqrt{-1}$$
を使えば、
\begin{align}
\sqrt{-a} &= \sqrt{-1}\sqrt{a} \\
&= i\sqrt{a}
\end{align}
とできるからです。
この式が成り立っているかを確認するには、\(\sqrt{-a}=i\sqrt{a}\)の両辺を\(2\)乗してみましょう。
\begin{align}
(\sqrt{-a})^2 &= (i\sqrt{a})^2 \\
-a &= i^2 a \\
-a &= -a
\end{align}
となります。
途中で、
$$i^2 = -1$$
を使っています。
つまり、複素数を定義するとルートの中にマイナスがあってもOK!になるのです。
実際の数字を当てはめてみると、
\begin{align}
\sqrt{-2} &= i\sqrt{2} \\
(\sqrt{-2})^2 &= (i\sqrt{2})^2 \\
-2 &= i^2 2\\
-2 &= -2 \\
\end{align}
のような感じです。
複素数が登場する因数分解を解く
では、実際に因数分解をしていきましょう。
以下の問題を解いていきます。
\(x^2-2x+4\)を複素数の範囲で因数分解せよ。
これは、解の公式を使って因数分解するパターンの問題ですね。
これを忘れた人は、以下のページから復習しましょう。
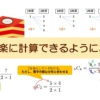
まずは、\(x^2-2x+4=0\)とおいて方程式の解を求めます。
解の公式を使うと、以下の式のように計算できます。
\begin{align}
x &= \frac{-b \pm \sqrt{b^2-4ac}}{2a} \\
&= \frac{-(-2) \pm \sqrt{(-2)^2-4 \cdot 1 \cdot 4}}{2 \cdot 1} \\
&= \frac{2 \pm \sqrt{-12}}{2} \\
&= \frac{2 \pm \sqrt{-1}\sqrt{12}}{2} \\
&= \frac{2 \pm i \sqrt{12}}{2} \\
&= 1 \pm i \sqrt{3}
\end{align}
上の式のように解の公式を使って解いていくと、ルートの中に\(-12\)が現れます。
先ほど虚数\(i\)を学びましたので、
$$i = \sqrt{-1}$$
となり、ルートの中からマイナスを消し、ルートの外に虚数単位\(i\)を付け加えます。
\(i\)を使うことにより、ルートの中のマイナスが削除できたので、このまま計算していきましょう。
この方程式の解は、
$$x = 1 \pm i \sqrt{3}$$
でした。
したがって、\(x^2-2x+4\)を因数分解すると、
\begin{align}
x^2-2x+4 = (x–1-i\sqrt{3})(x–1+i\sqrt{3})
\end{align}
となります。
最後に解の符号を変えることに気をつけましょう。
最後の計算過程が分からない人は、以下の記事で復習しておきましょう。
いかがでしたか。
以上で複素数の範囲での因数分解は完了です。
スポンサーリンク
まとめ
ここでは、はじめに虚数単位と複素数について簡単に説明しました。
その後、複素数の範囲での因数分解の解き方を解説してきました。
複素数は概念が難しい単元です。
「複素数とは何か?」に悩みすぎて進めないときは、一度、「そういうものだ」とわりきって、とりあえずは問題を解けるようにするのが良いでしょう。
では、以下に重要なポイントをまとめて終わります。
- 複素数は実数と虚数をあわせた数である
- 虚数単位\(i\) は2乗すると\(\sqrt{-1}\)になる数であり、\(i=\sqrt{-1}\)と覚えておく
- \(i\)を使うと複素数の範囲でも因数分解ができる

























ディスカッション
コメント一覧
まだ、コメントがありません