【高校数学（三角比）】三角比を使った三角形の面積の求め方 – sin, cos, ヘロンの公式を使った方法
- 三角比を使った三角形の面積の求め方を知りたい
- 三角比の公式は知っているが使い方がわからない
- 三角形の面積を求めるための、色々な方法を知りたい
三角比（\(\sin, \cos, \tan\)）を使った三角形の面積を求める方法はいくつかパターンがあります。
面積を求めた三角形についてどの情報が分かっているか（辺の長さがわかっているのか、角度がわかっているのか、など）によって、使用するパターンを適切に選ぶ必要があります。
ここでは、まずは基本である\(\sin\)を使った方法を紹介します。
その後、\(\cos\)を使った方法とヘロンの公式というものを使った方法まで丁寧に解説していきます。
三角比を用いた三角形の面積の求め方
三角形の面積の求め方といえば、小学校で習う、
$$\text{底辺} \times \text{高さ} \div 2 = \frac{1}{2} \times \text{底辺} \times \text{高さ}$$
が有名ですよね。
実は三角比を利用することで三角形の面積を求められます。
三角比を利用した三角形の求め方にはいくつかパターンがあるので、以下では一つずつ丁寧に紹介していきましょう。
まずは、始めに紹介する\(sin\)（サイン）を使った方法を覚えるとよいですよ。
スポンサーリンク
\(\sin\)（サイン）を使った面積の求め方
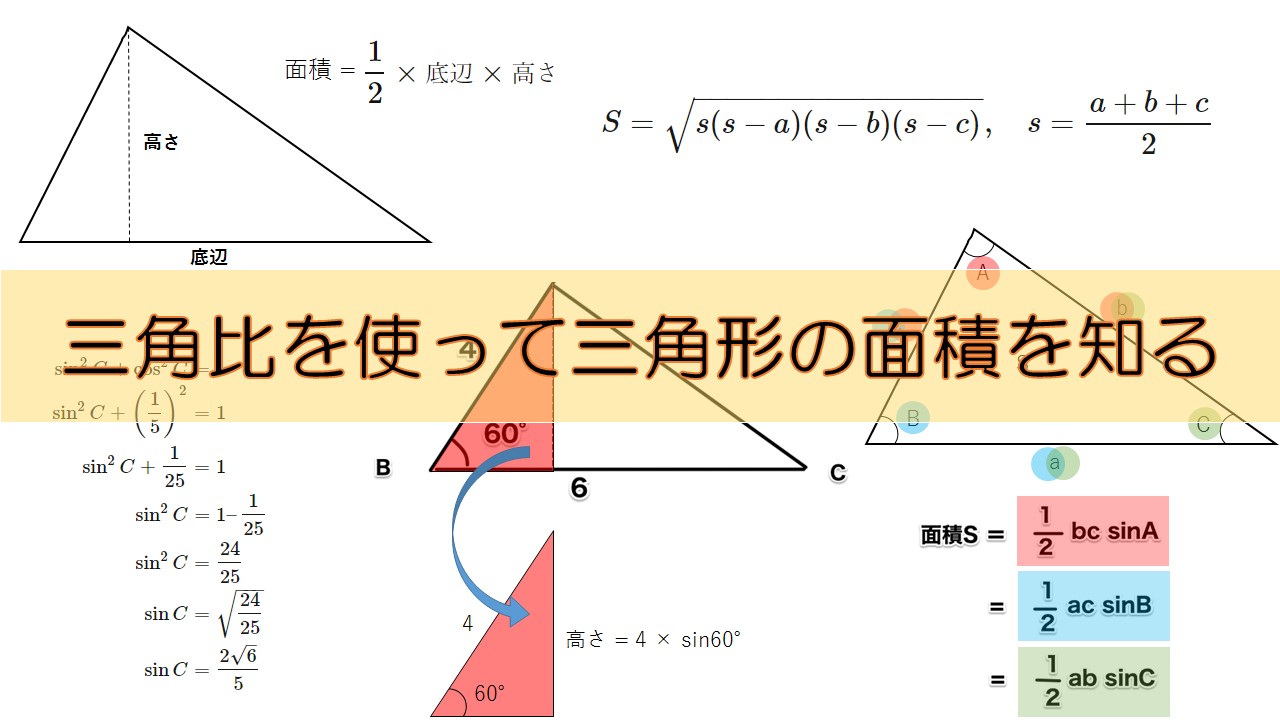
まず、下の図のような三角形があったとしましょう。
分かっている情報は、各辺の長さと角度です。
このとき、三角形の面積\(S\)を求めましょう。
ここで、
$$S = \frac{1}{2} \times \text{底辺} \times \text{高さ}$$
の公式を使おうとすると、
「高さがわからない三角形の面積は求められない！」
となってしまいます。
そんな時は三角比の\(\sin\)（サイン）を使うことで解決できます。
下の公式を見てみましょう。
使用するのは、2辺の長さとその間の角度です。
三角比を用いた公式では高さを必要としません。
三つ公式がありますが、回転させればどれも同じことを表現しているということがわかるでしょう。
要は、長さが分かっている2辺の間の角度を使えばよいのです。
ですので、三つのうちどれか一つを覚えれば十分です。
難しい公式ではないので、覚えてしまいましょう。
問題を解いて使い方を練習しよう
実際に問題を解いてみましょう。
角度\(B=60^{\circ}\), \(AB=4\), \(BC=6\)とする。
三角形の面積\(S\)を求めよ。
この問題を見たときに高さの情報がないですよね。
こういった場合は、三角比を使って面積を求めるのだと考えてください。
それぞれ、2辺の長さを
\begin{align}
AB=c=4 \\
BC=a=6
\end{align}
とします。
そして、上で覚えた三角形の面積の公式、
\begin{align}
S = \frac{1}{2} a c \sin{B}
\end{align}
に代入しましょう。
すると、
\begin{align}
S &= \frac{1}{2} \times 6 \times 4 \times \sin{60} \\
&= \frac{1}{2} \times 6 \times 4 \times \frac{\sqrt{3}}{2} \\
&= 6 \sqrt{3}
\end{align}
となります。
よって、三角形ABCの面積は\(6 \sqrt{3}\)ということになります。
三角比を利用すれば、高さがわからない三角形の面積を求められることがわかりましたね。
この公式は三角比で三角形の面積を求めるための一番基本の式ですので、必ず覚えておきましょう！
なぜこの公式で面積が求まるのかを証明
しかしなぜ、
\begin{align}
S & = \frac{1}{2} b c \sin{A} \\
& = \frac{1}{2} a c \sin{B} \\
& = \frac{1}{2} b a \sin{C}
\end{align}
という公式で三角形の面積が求められるのでしょうか？
それを証明していきましょう。
といってもすぐに分かります。
もう一度の例題①の三角形を見てみましょう。
これに以下の図のように赤線で高さを引いてみます。
では、この高さはどのようにして求められるでしょうか？
それは、線を引くことでできた左側の直角三角形を考えればよいですね。
よって、高さは、
\begin{align}
\text{高さ} = 4 \times \sin{60^{\circ}}
\end{align}
となります。
あとは、底辺×高さ÷2をすれば面積となりますので、
\begin{align}
\text{面積} &= \frac{1}{2} \times \text{底辺} \times \text{高さ}
&= \frac{1}{2} \times 6 \times 4 \sin{60^{\circ}}
\end{align}
となります。
これを記号で書けば、面積\(S\)は、
\begin{align}
S &= \frac{1}{2} \times a \times c \sin{B} \\
&= \frac{1}{2} a c \sin{B}
\end{align}
となり、三角比\(\sin\)で表現した面積の公式が登場しました。
すなわち、三角比を使った三角形の面積公式も、同じように、
$$\frac{1}{2} \times \text{底辺} \times \text{高さ}$$
をしているだけということですね。
\(\cos\)（コサイン）を使った面積の求め方
三角比は\(\sin\)だけではありません。
\(\sin\)の対になるものとして、\(\cos\)があります。
今度は\(\cos\)を使って三角形の面積を求める方法を紹介します。
\(\sin\)を使って三角形の面積を求めることができるのは、
2辺の長さとその間の角度
が分かっているときでしたね。
\(\cos\)を使って三角形の面積を求める場合は、次の情報がわかっているときです。
3辺の長さ
が分かっているときです。
辺の長さがすべて分かっていれば、角度は必要ありません。
そして、使う公式は”余弦定理”です。以下のような公式でしたね。
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A} \\
b^2 &= c^2 + a^2 – 2ca \cos{B} \\
c^2 &= a^2 + b^2 – 2ab \cos{C}
\end{align}
「余弦定理を忘れた」もしくは「そんなん知らん！」という人は、以下のページから確認して戻ってきてください↓
https://analytics-notty.tech/prove-the-formula-of-the-cosine-theorem/
cos（コサイン）を使って面積を求めてみる
では、以下のような例題を考えましょう。
以下のような三角形があります。
この三角形の面積を求めなさい。
3辺の長さがすべて分かっていますね。一方、角度は一つも分かっていません。
こんなときに\(\cos\)を使った余弦定理で面積を求めていきます。
まず、∠ACBを角度\(C\)とおきましょう。
すると、余弦定理、
\begin{align}
c^2 = a^2 + b^2 – 2ab \cos{C}
\end{align}
が使えます。
この中で辺の長さである\(a, b, c\)は分かります。
\begin{align}
a = 7 \\
b = 6 \\
b = 5
\end{align}
ですね。
分からないのは\(\cos{C}\)ですので、これを左辺にした式に変形しましょう。
すると、
\begin{align}
\cos{C} = \frac{a^2 + b^2 – c^2}{2ab}
\end{align}
となります。
これも余弦定理の有名な形の一つです。
そして、\(a, b, c\)を代入しましょう。
\begin{align}
\cos{C} &= \frac{5^2 + 6^2 – 7^2}{2 \cdot 5 \cdot 6} \\
&= \frac{12}{60} \\
&= \frac{1}{5}
\end{align}
です。
次に、\(\cos\)を\(\sin\)に直しましょう。
その理由は、\(\sin{C}\)が分かれば、このページの最初に紹介した\(\sin\)を使った面積の公式、
$$S=\frac{1}{2} a b \sin{C}$$
に代入して面積を求めることができるからです。
\(\cos\)を\(\sin\)に直すには、もう一つ、以下の公式を使います。
$$\sin^2{\theta} + \cos^2{\theta} = 1$$
この式の\(\theta\)を\(C\)にして、上で求めた\(\cos{C}=\frac{1}{5}\)を代入してみましょう。
すると、
\begin{align}
\sin^2{C} + \cos^2{C} &= 1 \\
\sin^2{C} + \left( \frac{1}{5} \right)^2 &= 1 \\
\sin^2{C} + \frac{1}{25} &= 1 \\
\sin^2{C} &= 1 – \frac{1}{25} \\
\sin^2{C} &= \frac{24}{25} \\
\sin{C} &= \sqrt{\frac{24}{25}} \\
\sin{C} &= \frac{2\sqrt{6}}{5}
\end{align}
です。
よって、これと\(a=7, b=6\)を、
$$S=\frac{1}{2} a b \sin{C}$$
に代入して面積を求めると、
\begin{align}
S &= \frac{1}{2} a b \sin{C} \\
&= \frac{1}{2} \cdot 7 \cdot 6 \cdot \frac{2\sqrt{6}}{5} \\
&= 6 \sqrt{6}
\end{align}
となり、問題の三角形の面積は\(6 \sqrt{6}\)となります。
このように、三角形の3辺の長さがすべてが分かっていて、角度が一つも分かっていないときは、余弦定理で\(\cos\)を使った方法から面積を求めることができます。
結局最後は、\(sin\)を使った面積の公式に当てはめて答えを求めますので、計算量は多いです。
可能であれば、はじめに紹介した\(sin\)を使った方法を使うほうがよいでしょう。
スポンサーリンク
ヘロンの公式を使って三角形の面積を求める
最後は、ヘロンの公式を使った三角形の面積を求める方法です。
ヘロンの公式はマイナーな公式なので、
「はじめて聞いた。」
という人もいるかもしれません。
この公式は、前に説明した\(\cos\)を使用して面積を求める方法を、もっと簡単にするために作られたものです。
ですので、面積を求める三角形は3辺の長さがすべてわかっているものが対象となります。
【ヘロンの公式を使える三角形：3辺の長さがすべてわかっている】
ヘロンの公式は以下のようなものです。
3辺の長さをそれぞれ\(a, b, c\)として、
\begin{align}
S = \sqrt{s(s-a)(s-b)(s-c)}, \quad s=\frac{a+b+c}{2}
\end{align}
必要なのは長さだけであることがわかります。角度は登場しません。
意外と覚えやすい公式なので、覚えてしまうのもありです。きっとテストで役に立ちます。
では、ヘロンの公式を使って前回の例題②を解いてみましょう。
以下のような三角形があります。
この三角形の面積を求めなさい。
3辺の長さがすべてわかっているので、以下のヘロンの公式に代入するだけです。
\begin{align}
S = \sqrt{s(s-a)(s-b)(s-c)}, \quad s=\frac{a+b+c}{2}
\end{align}
まずは、\(s\)から求めましょう。
\begin{align}
s &= \frac{a+b+c}{2} \\
&= \frac{5+6+7}{2} \\
&= 9
\end{align}
次に、\(S\)を求めましょう。
\begin{align}
S &= \sqrt{s(s-a)(s-b)(s-c)} \\
&= \sqrt{9(9-5)(9-6)(9-7)} \\
&= \sqrt{9 \cdot 4 \cdot 3 \cdot 2} \\
&= 6 \sqrt{6}
\end{align}
よって、三角形の面積は\(6\sqrt{6}\)と求まりました。
前回の\(\cos\)を使って求める方法と比べると、圧倒的に簡単に計算できてしまいます。
ぜひ、ヘロンの公式を使えるようになりましょう。
もっと詳しく知りたい人は、以下のページがオススメです↓
https://analytics-notty.tech/find-the-area-of-the-triangle-with-herons...
以上で、三角比を使って三角形を求める方法の紹介を終わります。
お疲れさまでした。
まとめ
ここでは、三角比を使った三角形の面積の求め方の三つの方法を紹介しました。
※ヘロンの公式は直接は三角比を使ってませんが…
一番の基本は、始めの\(\sin\)を使った方法です。
まずは、ここからできるようになりましょう。
次は、\(\cos\)を使った方法を学びました。
しかし、これはなかなか計算量が多かったですね。
なので、これの代わりにヘロンの公式を覚えるというのも一つの手です。
最終的には、すべての方法を使えるようになり、三角形の情報から適切に方法を選べるようになりましょう。
それでは、さようなら。