【高校数学(三角比)】余弦定理の公式を証明 – 図を使って丁寧に説明
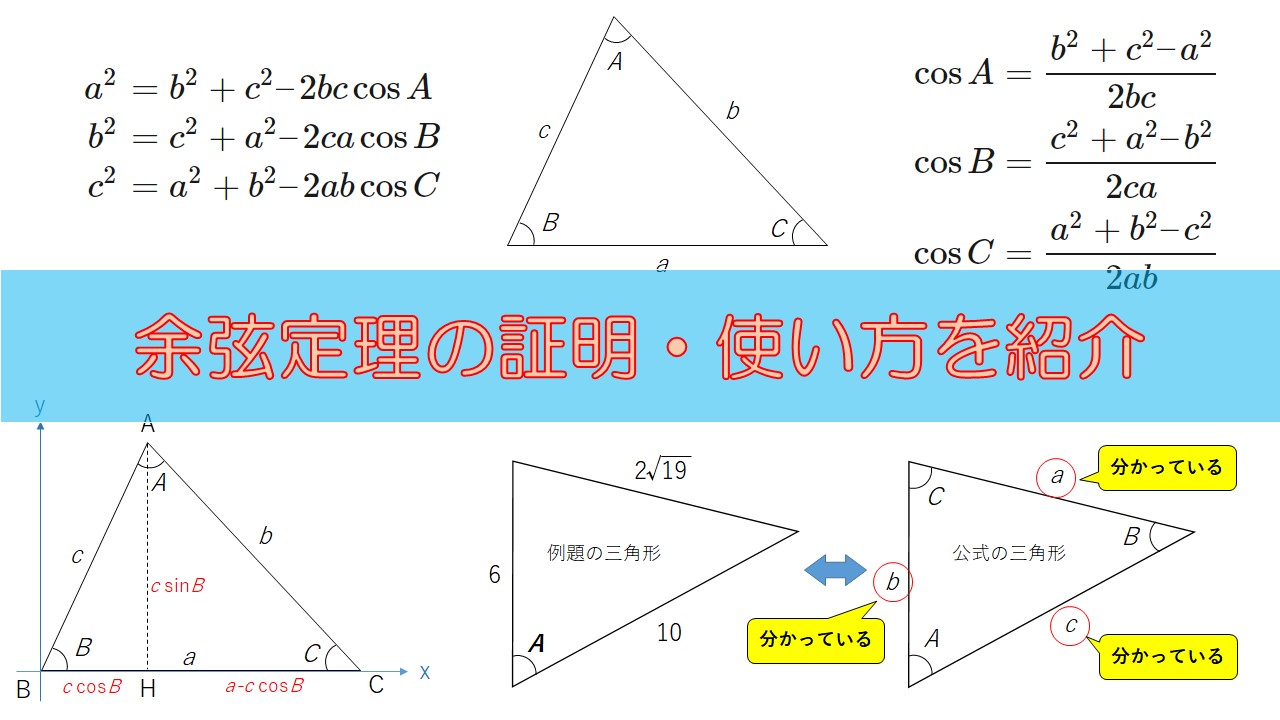
余弦定理の公式
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A} \\
b^2 &= c^2 + a^2 – 2ca \cos{B} \\
c^2 &= a^2 + b^2 – 2ab \cos{C}
\end{align}
を、図を使って丁寧に証明します。
また後半には、公式を使って実際に例題を解く方法を紹介します。
余弦定理の公式とは
余弦定理とは、三角関数に関する公式であり、以下のようなものです。
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A} \\
b^2 &= c^2 + a^2 – 2ca \cos{B} \\
c^2 &= a^2 + b^2 – 2ab \cos{C}
\end{align}
\(a\), \(b\), \(c\)は三角形の各辺の長さ、\(A\), \(B\), \(C\)はそれらの辺の対角の角度を表しています。

上では余弦定理として、\(a\), \(b\), \(c\)に関する三つの式を示しました。
しかし、三つの式は互いに対称性があるため、どれか一つを覚えておけばオッケーです。
また、上の式の左辺は\(a^2\), \(b^2\), \(c^2\)であり、辺の長さの二乗となっています。
ですので、長さを求めるときには有効です。
一方、三角形の角度を求めたいときは、上の式を少し変形して次の公式が使われます。
\begin{align}
\cos{A} &= \frac{b^2 + c^2 – a^2}{2bc} \\
\cos{B} &= \frac{c^2 + a^2 – b^2}{2ca} \\
\cos{C} &= \frac{a^2 + b^2 – c^2}{2ab}
\end{align}
初めの式から、ただいくつか項を移項して左辺にコサインを持ってきただけです。
この式は、右辺に辺の長さだけの情報を置きましたので、辺の長さがわかっているときに角度を求めるのに便利です。
これらの公式の使い方はこの記事の後半で紹介します。
スポンサーリンク
余弦定理の証明
では、この記事のメインである余弦定理の公式の証明をしましょう。
まずは、以下の図のように三角形を座標の上に配置しましょう。
次に、下の図に示す赤い点の座標を考えます。
そのためには、赤い点からx軸へ垂線を引きましょう。
垂線をx軸が交わった点をHとします。
三角形ABHに注目すると、赤い点の座標がわかります(以下の図を参照してください。)。
\begin{align}
AH = c \sin{B} \\
BH = c \cos{B} \\
\end{align}
ここまでで分かっている辺の長さを図に描くと、以下のようになります。
次に、三角形AHCに注目します。
この三角形は直角三角形であり、三辺の長さがすべてわかっていますので、三平方の定理が成り立ちます。
\begin{align}
b^2 & = (c\sin{B})^2 + (a-c\cos{B})^2 \\
& = c^2 \sin^2{B} + a^2 – ac\cos{B} + c^2 \cos^2{B} \\
& = c^2 (\sin^2{B} + \cos^2{B}) + a^2 – ac\cos{B} \\
& = c^2 + a^2 – 2ac\cos{B}
\end{align}
これで、余弦定理の公式が導かれました!
\(a\), \(b\), \(c\)の順番を変えれば、同じようにすべての余弦定理の公式が導けることがわかりますね。
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A} \\
b^2 &= c^2 + a^2 – 2ca \cos{B} \\
c^2 &= a^2 + b^2 – 2ab \cos{C}
\end{align}
余弦定理の公式の使い方
証明も終わったことですし、最後に余弦定理の公式の基本的な使い方を紹介しておわります。
はじめに述べたように、余弦定理の公式は三角形の
- 長さを求めるため
- 角度を求めるため
の二つの利用方法があります。
長さを求める問題は、
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A}
\end{align}
の公式を使います。
一方、角度を求める問題には、
\begin{align}
\cos{A} &= \frac{b^2 + c^2 – a^2}{2bc}
\end{align}
の公式を使います。
長さを求めるための使い方
まずは、長さを求めるための公式の使い方からです。
以下のような例題を考えましょう。
以下のような三角形があります。
\(a\)の長さを求めなさい。
という問題です。
この問題は長さを求める公式ですね。
ですので公式は、
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A}
\end{align}
の方を使用しましょう。
\(a\)以外の長さ\(b\), \(c\)と、\(a\)の対角の角度\(A\)がわかっています。
\begin{align}
b &= 8 \\
c &= 6 \\
A &= 60^{\circ}
\end{align}
これらの値を公式に代入すると、
\begin{align}
a^2 &= b^2 + c^2 – 2bc \cos{A} \\
&= 8^2 + 6^2 – 2 \times 8 \times 6 \times \cos{60^{\circ}} \\
&= 64 + 36 – 96 \times \frac{1}{2} \\
&= 52
\end{align}
ですので、\(a\)の長さは、
$$a = \sqrt{52} = 2 \sqrt{13}$$
と求まります。
角度を求めるための使い方
次は、角度を求めるための使い方を習得しましょう。
例題は以下のようなものです。
以下のような三角形があります。
角度\(A\)を求めなさい。
こんどは、三角形の三辺の長さがすべて分かっているときに、角度を求める問題です。
角度を求める問題のときは、次の公式を使います。
\begin{align}
\cos{A} = \frac{b^2 + c^2 – a^2}{2bc}
\end{align}
公式の右辺の\(a\), \(b\), \(c\)はすべてわかっています。
\begin{align}
a &= 2 \sqrt{19} \\
b &= 6 \\
c &= 10
\end{align}
あとは公式に代入するだけです。
\begin{align}
\cos{A} & = \frac{b^2 + c^2 – a^2}{2bc} \\
& = \frac{6^2 + 10^2 – (2 \sqrt{19})^2}{2 \times 6 \times 10} \\
& = \frac{36 + 100 – 76}{120} \\
& = \frac{1}{2}
\end{align}
よって、角度\(A\)は、
\begin{align}
\cos{A} & = \frac{1}{2} \\
A & = 60^{\circ}
\end{align}
となり、答えは\(A=60^{\circ}\)です。
スポンサーリンク
まとめ
- 余弦定理とは、三角形の長さや角度を求めるための公式
- 求めたいのが長さか角度かによって、2パターンの余弦定理を使い分ける必要がある
- 余弦定理がなぜ成り立つかを図を使って丁寧に証明した
- 練習問題を解いて余弦定理に慣れていこう


























ディスカッション
コメント一覧
余弦定理途中の式が違っている気がします(A-B)の二乗はA二乗-2AB+B二乗ですが2が抜けているように感じます(公式になったら2を付け加えていますが、、、、)
間違いのご指摘ありがとうございます。
修正しました。また、間違いがあったら教えてもらえると嬉しいです。