【数学クイズ・パズル】AA+BB+CC=ABCが成り立つA、B、Cは何?
数式に関する数学パズルです。
文字だけで構成された以下の数式をを満たす数字を見つけましょう。
$$AA + BB + CC = ABC$$
数式に関する数学パズル
問題
問題です。
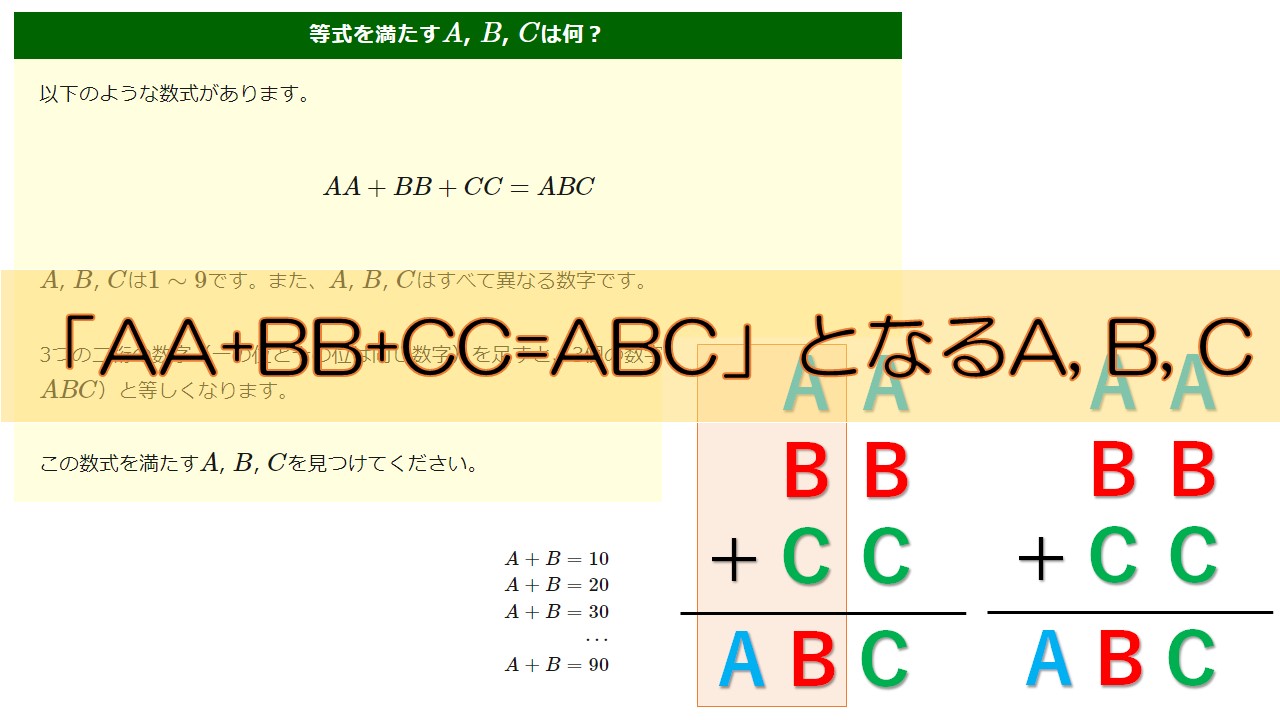
以下のような数式があります。
$$AA + BB + CC = ABC$$
\(A\), \(B\), \(C\)は\(1 \sim 9\)です。また、\(A\), \(B\), \(C\)はすべて異なる数字です。
3つの二桁の数字(一の位と十の位は同じ数字)を足すと、3個の数字が並んだ3桁の数字(\(ABC\))と等しくなります。
この数式を満たす\(A\), \(B\), \(C\)を見つけてください。
以下では、まずヒントを示します。
自力で考えたい人はスクロールをしすぎないように注意してくださいね。
ヒント
ヒントです。
\(ABC\)としてできる3桁の最大数は何でしょうか?
$$A=9, \quad B=8, \quad C=7$$
とすると、
$$99+88+77=264$$
これより大きな3桁の数はありません。※\(A, B, C\)はそれぞれ異なる数字が入ることに注意してください。
つまり、\(ABC\)として作られる数は、200台か100台の数ということですね。
よって、百の位の\(A\)は\(1\)か\(2\)です。
$$A=1 \quad \text{もしくは} \quad A=2$$
ヒントはここまでです。では、続きをどうぞ。
解答
では、解答です。もう一度問題を書いておきます。
$$AA + BB + CC = ABC$$
ただし、\(A\), \(B\), \(C\)は\(1 \sim 9\)であり、\(A\), \(B\), \(C\)はすべて異なる数字です。
繰り上がりの計算がある可能性も頭に入れて考えましょう。
まずは一の位の計算に注目しよう
まず、一の位を考えます。
一の位は上の図からわかるように、以下の式が成り立ちます。
$$A + B + C = C$$
この式から\(C\)を消去すると、
\begin{align}
A + B + C & = C \\
A + B & = 0 \\
\end{align}
であり、\(A+B\)は\(0\)となります。
ですので、繰り上がりを考えると、
\begin{align}
A + B = 10 \\
A + B = 20 \\
A + B = 30 \\
\cdots \\
A + B = 90
\end{align}
となれば良さそうです。
ところで、ヒントで述べたように、\(ABC\)は200台か100台の数ということでした。
したがって、\(A=1\)か\(A=2\)です。
そこで、\(B\)として入る数の最大値は\(9\)ですから、\(A+B\)の最大の数は、
$$A+B=2+9=11$$
となります。
\(11\)より小さく一の位が\(0\)となるのは\(10\)しかありませんので、
$$A+B=10$$
で確定です。
そうなると、\(B\)も絞られてきます。
\(A=1\)か\(A=2\)ですので、\(A+B=10\)を満たすには、
\begin{align}
1+9 &= 10 \\
2+8 &= 10
\end{align}
のどちらかです。
つまり、
- \(A=1\)であり\(B=9\)
- \(A=2\)であり\(B=8\)
の2つのペアのどちらかであるということがわかります。
十の位の計算から答えを絞りこもう
次に、十の位を考えます。
ここで、十の位には一の位から\(1\)が繰り上がっていること忘れずに(\(A+B=10\)でしたからね)。
つまり、十の位の計算は
$$A + B + C + 1 = AB$$
となります。
- \(A=1\)であり\(B=9\)
- \(A=2\)であり\(B=8\)
まで絞られていたので、まずは、\(A=2\)の場合が適当か調べてみましょう。
\(B=8\)ですから、
$$2+8+C+1=28$$
です。
これを計算すると、
\begin{align}
2+8+C+1 &= 28 \\
C &= 17
\end{align}
\(C=17\)となり、二桁の数になります。
完全に矛盾しますね。\(A=2, B=8\)の場合はダメなようです。
そこで、次は,
$$A=1, \quad B=9$$
を考えてみましょう。
先ほどの、
$$A+B+C+1=B$$
において、同様に\(A\)と\(A\)を代入すると、
$$1+9+C+1=19$$
です。
ゆえに、
$$C=8$$
であり、\(A\), \(B\), \(C\)が確定しました。
$$A=1, \quad B=9, \quad C=8$$
です。
これらを問題の式に代入してみましょう。
\begin{align}
AA + BB + CC &= ABC \\
11 + 99 + 88 &= 198
\end{align}
やりました!ちゃんと成り立っていますね。
スポンサーリンク
数式パズルに対する考察
数式が登場する数学パズルで、このような数字がきれいにそろうタイプの問題では、解き方のアプローチとして、
「できうる最大の数をまず考えてみる」
というのがありそうです。
例えば、類似の数学パズルとして、以下のような問題も紹介しています。
ここでも、
「まず、考えられる最大の数から数字の候補を絞る」
という操作をしています。
数学パズルには、問題の種類によって解き方・アプローチの仕方にコツがあります。
例えば数学の図形の問題では、「補助線を引いてみる」というコツがありますよね。
このようなちょっと数学ちっくな問題が好きな人は、以下のページもチェックしてみてください。ページ内の「ちょっと数学的」という項目です↓
まとめ
- 数式が登場する数学パズルで、数字がきれいにそろうタイプの問題を紹介した
- 解くためのはじめのアプローチとして、考えられる最大の数から数字の候補を絞るということが有効
- 数学パズルには、問題の種類によって解き方・アプローチの仕方にコツがある


























ディスカッション
コメント一覧
問題を
10a+a+10b+b+10c+c=100a+10b+c
にしたほうがいいと思います
a+b+c=cになると書いてあるが、繰り上がりがあるので成り立たない。
よってa+ b=0には必ずしもできない。
1の位の解説の時に100の位がaなのでa=1と置いてしまっても良いのでは?
ピンバック & トラックバック一覧
buy cbd oil
【数学クイズ・パズル】AA+BB+CC=ABCが成り立つA、B、Cは何? | 数学の面白いこと・役に立つことをまとめたサイト