【数学クイズ・パズル】天秤を使って重さの違う金貨をみつけよう
天秤を使って仲間はずれの金貨1枚を見つける数学パズルです。
ここでは、その中から2問紹介したいと思います。はじめの問題は、肩慣らしです。素直に考えれば解けます。
二問目は少し難易度が上がります。柔軟に頭を使う必要があるでしょう。…といってもひっかけ問題ではありません。特別な操作をせず、ルールにのっとって考えていけば解けます。
金貨9枚の中から天秤を使って違う重さのものをみつけよう
まずは、頭のウォーミングアップから始めましょう。
問題
ここに9枚の金貨があります。8枚の重さは10gですが、1枚だけ9gの金貨が混じっていますが、見た目ではまったく区別できません。
天秤を二回だけ使って重さの異なる金貨を見つけてください。
まずは、簡単な問題からです。どのようにすれば、よいでしょうか？
以下、解答なので自力で解きたい人は、見ないように気をつけてください。
解答
まず、9枚の金貨を3枚ずつの3グループに分けます。
その中の二つのグループを天秤に乗せます。
もし天秤がどちらか傾いたら、軽いほうの三つの中に目的の9gがあるということがわかります。
では、天秤が釣りあった場合はどうでしょうか？そのときは、天秤に乗せてないグループのどれかが9gの金貨ということになります。
これで三枚まで金貨がしぼれたら、この三枚から一枚ずつを天秤に乗せます。
あとは、同じように判断すればよいでしょう。傾いたら軽い方が9gの金貨ですし、釣り合った場合は天秤に乗せてない金貨が9gの金貨ですね。
スポンサーリンク
金貨12枚の中から天秤を使って違う重さのものをみつけよう
次は結構難しいですよ。
問題
ここに12枚の金貨があります。11枚の重さは同じですが、残り1枚は重さが違います。（重さの違う金貨を偽物と呼びます）
ただし、今回は偽物の金貨が他の金貨と比べて軽いのか重いのかはわかりません。
天秤を三回だけ使って重さの異なる偽物金貨を見つけてください。
今度は、金貨の数が増えました。さらに、偽物は軽いか重いかわかっていません。計る回数は三回です。
さあ、どうしましょう。
以下、解答です。
解答
はじめに、4枚ずつの三グループに分けます。
この三グループをA、B、Cグループとしましょう。
AとBグループを天秤に乗せます（１回目の測定）。
一回目の測定でAとBグループの金貨が釣り合った場合
このとき、もし天秤が釣り合ったら、残りのCグループの中に重さの違う金貨があります。
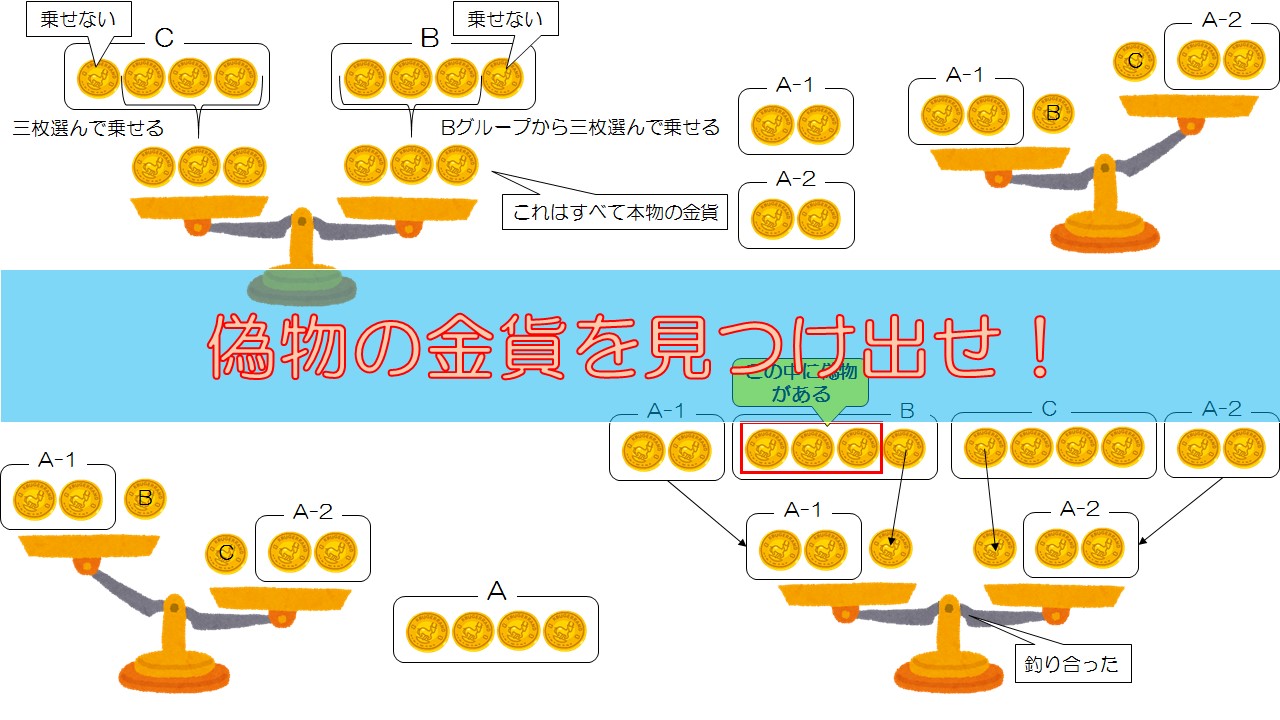
残りのCグループから金貨を三つ選び天秤に乗せます（二回目の測定）。もう片側には、Bグループ（Aグループでもよい）から三つを選び乗せます。
ここで、Bグループの金貨はすべて本物のはずですね。AとBグループは釣り合ったのですから。
このとき、天秤が釣り合えば乗せてないCグループの金貨が偽物だとわかります。
天秤が傾いた場合、Cグループの天秤に乗せた三枚のどれかが偽物だということになります。
そして、ここが重要ですが、Cグループが軽かった場合は偽物金貨は軽い、Cグループが重かった場合は偽物金貨は思い、ということが分かります。ここではじめて偽物金貨が軽いか重いかが分かるのです。
後は、三回目の測定として、Cグループの天秤に乗せた三枚の金貨から下の図のように、一枚ずつ乗せて、
釣り合えば、天秤に乗せてない金貨が偽物、傾いたら偽物金貨の重さが軽いか重いかを判断して（二回目の測定でわかっている）、そちらが偽物ということになります。
一回目の測定でAとBグループの金貨が傾いた場合
一回目の測定で天秤が傾いたら、AグループもしくはBグループの中に重さの違う偽物金貨があります。この場合が少し厄介です。
ここでは、Aグループの方が軽かったとしてここから先の話を進めていきます。Bグループの方が軽かった場合でも以下の説明のAとBを入れ替えるだけで両方対応できます。
Aグループの金貨をA-1とA-2グループの二つに2枚ずつ分けます。
そして、「A-1グループとBグループから1枚取り出した3枚」と「A-2グループとCグループから1枚取り出した3枚」を天秤に乗せます（二回目の測定）。
このとき天秤が釣り合ったら、Bグループの天秤に乗せなかった三枚のうちどれかに偽物があるということになります。
なぜなら、上で天秤に乗せた金貨はすべて本物ですし（本物でなければ釣り合わない）、Cグループの金貨は一回目の測定ですべて本物ということが分かっているからです。
偽物候補が三枚に絞られれば後は簡単です。一枚ずつ天秤に乗せ釣り合えば、天秤に乗せてない金貨が偽物です。
天秤が傾いたら、偽物が軽いのか重いのかを判断しましょう。一回目の測定を思い出してください。Bグループの方がAグループより軽かったですよね。
Aグループは全て本物であることが、さっきの測定から分かったので、偽物金貨の重さは軽いのです。よって軽い方が偽物ですね。
最後に二回目の測定で天秤が傾いた場合ですね。その前に二回目の測定がどのような測り方をしたかを下の図で思い出しましょう。
このような感じでした。
これが、Bグループの金貨を乗せた方が重かったとします。
このとき、一回目の測定結果を思い出してください。BグループがAグループよりも重かったですよね。
ということは、上の天秤で考えると、Bが重いかA-2の中のどれかが偽物ということになります。なぜなら、Cは本物ということが分かっていますし、A-1の金貨が偽物であれば軽いはずですからね。
ということで、今天秤に乗っているBかA-2の三枚に絞られます。三枚に絞られれば後は簡単ですね。
A-2の二枚を一枚ずつ天秤に乗せましょう。Aグループに偽物があれば、その偽物は軽いはずですので軽いほうが偽物です。釣り合えば、天秤に乗せていないBが偽物です。
最後の最後です。二回目の測定でCの金貨が乗っているほうが重かった場合はどうでしょう。
これも先ほどの考え方と同様です。もしBが偽物なら天秤は左が下がっているはずです。なぜなら、一回目の測定でBはAよりも重いことが分かっているからです。A-2の中に偽物がないという理由の同じ理由から分かります。
ということは、A-1の中に偽物があるということです。あとは、A-1を一つずつ天秤に乗せて軽い方が偽物ですね。
やっと、すべて解けました！これは、難しいですね。
もっと数学クイズやパズルについて知りたい人は、以下のページを是非ご覧ください。
https://analytics-notty.tech/mathematics-quiz-puzzle-all-articles-summ...
まとめ
- 9枚の金貨から偽物を見つけるのは、二回の測定で十分である
- 12枚の金貨から偽物を見つけるのは、三回の測定で十分である
- 偽物金貨の重量がわからないというのが、問題を難しくしている