9は不思議な数字 – 五つの9の数学的な性質について詳しく紹介
一桁の数字の中で9は不思議な性質をたくさん持っている特別な数字です。
ここでは、9の持つ面白くて、不思議な数学的な性質を余すことなく紹介していきたいと思います。
その①：必ず自分自身に戻ってくる不思議な現象
はじめに、一番わたしが好きな9の性質を紹介します。
これから簡単な計算を行いますが、電卓や携帯が近くにある人は一緒にやってみましょう。
まず、何でもいいので、適当な数字を電卓に入力しましょう。電卓でなくとも紙に書いて自分で計算してもよいですよ。何桁の数字でも構いません。
ここでは、
$$73$$
という数字を使います。
この数字に、”9″を掛けてください。
$$73 \times 9 = 657$$
ですね。次に、この数字の各桁の数字を足してください。
$$6 + 5 + 7 = 18$$
ですね。さらにもう一度、各桁の数字を足してください。
$$1 + 8 = 9$$
“9”になりました。はじめに適当な数字に掛けた数も9でしたね。これは偶然でしょうか。
もう一度やってみましょう。今度は、
$$113$$
です。これに9を掛けて、
$$113 \times 9 = 1017$$
です。この数字の各桁の数字を足して、
$$1 + 0 + 1 + 7 = 9$$
です。また9になりました。しかも今度は一回で戻ってきました。
そうです！どんな数字でも、次のような操作をすると、必ず9に戻ってきてしまうのです。
- 適当な数字に9を掛ける
- 操作1で出た数字の各桁を足す
- 操作2を一桁になるまで繰り返す
不思議ですよね。この性質は9以外の数字では成り立たないんです。”9″って何者ですかね。
スポンサーリンク
その②：9を足された数が持つ性質
またまた、一緒にやってみましょう。何か適当な数字を用意しましょう。
何桁でもいいのですが、あまりに大きな桁だと計算が面倒なので、はじめは2桁の数がいいでしょう。
ここでは、
$$26$$
を例に進めます。
26の各桁の足し算は、
$$2 + 6 = 8$$
ですね。
では、26に9を足した数はどうでしょうか。
$$26 + 9 = 35$$
であり、各桁を足すと、
$$3 + 5 = 8$$
です。この数は元の数と同じですね。
一桁でも同じです。
$$7$$
を試してみましょう。
7の各桁を足しますが、これは一桁しかないので、7です。
次に9を足した数を考えましょう。
$$7 + 9 = 16$$
各桁を足すと、
$$1 + 6 = 7$$
となりやっぱり同じ数になります。
まとめると、
ある数字の各桁の合計は、その数に9を足した数字の各桁の合計と等しくなる
ということです。
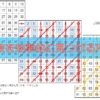
その③：9で割り切れるかはすぐにわかる
次は割り算が登場します。ここで紹介するのは、どんな大きな桁数の数字でも9で割り切れるかどうかがすぐに分かってしまうという9の性質です。
では、5桁くらいの大きな数字を一つ用意しましょう。ここでは、
$$25353$$
という数字を対象としてみます。
さて、みなさんはこの数字が9で割り切れるか瞬時に判断できますか？
ある方法を使えば三秒とかからず、判断できてしまいます。
もはや定番になってきましたが、すべての各桁の数字を足しましょう。
$$2 + 5 + 3 + 5 + 3 = 18$$
これを数字が一桁になるまで繰り返します。
$$1 + 8 = 9$$
最後は9になりましたね。このように最後に9になるものは9で割り切れるのです。
実際、25353を9で割ると、
$$25353 \div 9 = 2817$$
となりちゃんと割り切れることが確認できました。
ちなみに、一回の足し算が終わったとき18という数字がでてきました。
この時点でこの数字が9で割り切れる数字であれば、”9で割り切れる”と判断してもオッケーです。
では、問題です。次の二つの数字のうち、9で割り切れるのはどっちでしょうか？
$$111111111, \quad 111111$$
わかりましたか？
スポンサーリンク
その④：どんな数字も大きい方から小さい方を引いた数は必ず9で割り切れる
どんな数字でもよいので、一つの数字を準備してください。何桁の数字でもオッケーです。
ここでは4桁の数字、
$$4938$$
を使って説明します。
この数字にある操作を行うことで、9で割り切れるようになります。
まず、各桁の数字を比べて、大きい方の数から並べなおしてください。つまり、
$$4938 \rightarrow 9843$$
となります。次に逆に小さい方の数から並べなおした数も作ります。
$$4938 \rightarrow 3489$$
これで、二つの数字\(9843\)と\(3489\)ができました。この二つの数字の大きい方から小さい方の数を引きます。答えは、
$$9843 – 3489 = 6354$$
ですね。こうやってできた数は9で割り切ることができます。
「その③：9で割り切れるかはすぐにわかる」で紹介した方法で9で割り切ることができるか確認してみましょう。すべての桁の数を一桁になるまで足していけばよいですね。
$$6354 \rightarrow 6+3+5+4 = 18 \rightarrow 9$$
見事に9となりました。これで、6354は9で割り切れることが分かりました。
このように、
- ある数字を準備する
- その数字の各桁の数が大きい方から並べたものと小さい方から並べたものを作る
- 大きい方の数から小さい方の数を引く
- 上の操作で出てきた数は必ず9で割ることができる
が成り立ちます。
1桁の数を選んだ場合
1桁の数を選んだ場合は桁を並びかえることができませんね。このときは、十の位の数を0として考えてあげましょう。
例えば、\(7\)を考えるときは、
$$7 \rightarrow 07$$
と考えてやるのです。
すると、大きい方から並べた数は\(70\)であり、小さい方から並べた数は\(07\)として引き算ができます。
$$70 – 7 = 63$$
\(63\)という数がでてきました。これは明らかに9で割り切れる数ですね。
その⑤：電卓の数字の並びは9が存在している
電卓の数字の並びを確認してみましょう。下のような並びとなっていますよね。
この横一列の数字を足した数を考えてみましょう。
このように、横一列の数字の和は上から24、15、6となります。そして、それらの数の差は9です。
\begin{align}
24 – 15 & = 9 \\
15 – 6 & = 9
\end{align}
スポンサーリンク
まとめ
- 9を掛けた数は、各桁の数字を足して、それを一桁になるまで続けると最後は9となる
- ある数とその数に9を足した数の各桁の合計の数は等しくなる
- 各桁の数字を足して、それを一桁になるまで続ける。その数が9になれば元の数は9で割り切れる数である
- どんな数でも各桁の数字を大きい方から並べた数から小さい方から並べた数を引くと、9で割り切れる数となる
- 電卓の各横一列の数の合計の差は9である