素数をすばやく見つける方法 – エラトステネスのふるい

2018年2月18日2020年5月20日

古代ギリシャのエラトステネス

今から約2000年前、古代ギリシャにエラトステネスという数学者でもあり、天文学者、地理学者でもあった人物がいました。

彼は、数多くの学問で大きな功績を残しましたが、特にその中で有名なのが、

• 地球の大きさを高精度で測定した
• 素数を素早く見つける方法を発明した（エラトステネスのふるい）

の二つでしょう。

今回は、二つ目の”エラトステネスのふるい”について紹介します。

 

地球の大きさを高精度で測定した方法については以下の記事で詳しく紹介していますので、興味のある方はご覧ください。

 

スポンサーリンク

素数の特徴を復習しておこう

素数の特徴を復習しておきましょう。

素数の定義は、

1と自分自身で割り切れない、1以外の数

です。

例えば、”7″は1と7以外で割り切れる数がないですよね。ですので、7は素数となります。

一方、”4″は１と4以外にも2で割り切ることができます。ですので、”4″は素数ではありません。

 

また、重要な素数の性質として、1から数を増やしていき順番に素数を調べていくとき、素数は完全にランダムに登場します。

つまり、「3つおきに素数は現れる」などの規則性がないのです。

これが素数を探すことを難しくしている原因です。

余談ですが、素数に規則性がないおかげで、私たちの個人情報を犯罪から守ることができています。詳しくは、

をご覧ください。

 

”エラトステネスのふるい”はどんな方法？

素数を簡単に見つけるための”エラトステネスのふるい”とは、どんな方法でしょうか。

前に述べたように、素数はランダム現れます。そのため、一つずつ素数であるかをチェックしていく必要があるのですが、エラトステネスの時代は、当然パソコンのような自動で計算してくれるハイテクなものはありません。

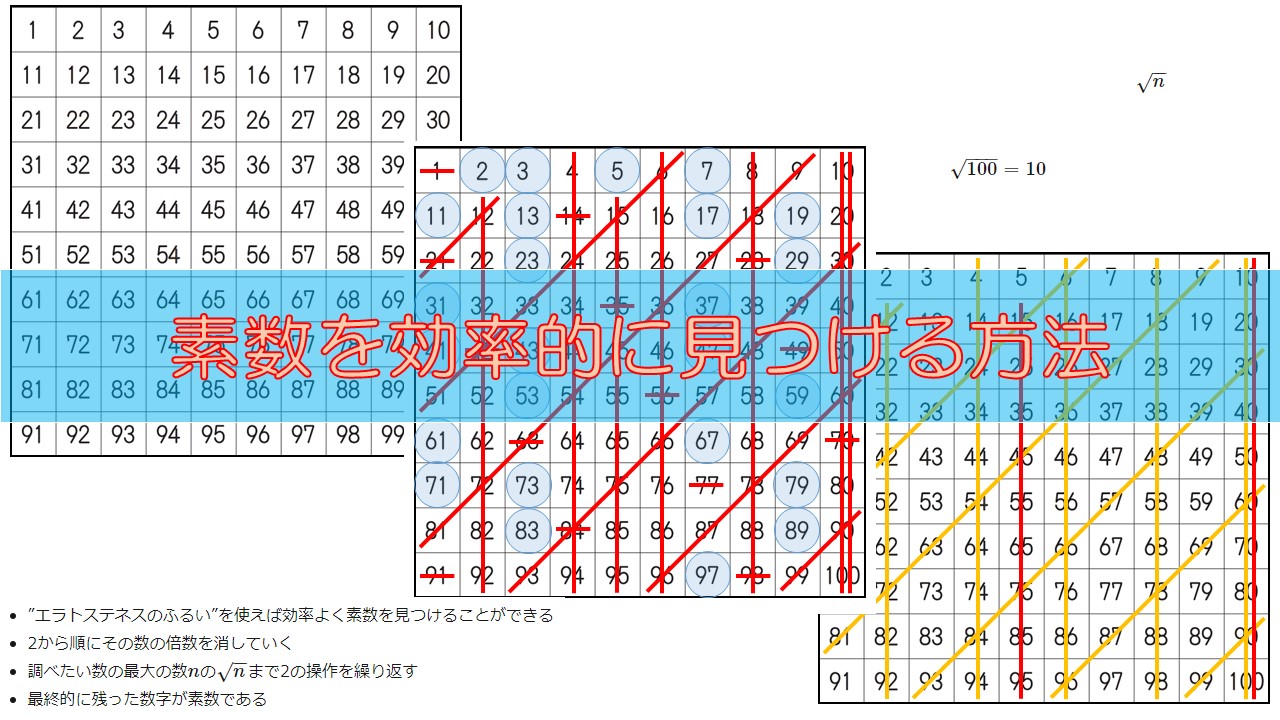
そこでエラトステネスが考えたのが、”エラトステネスのふるい”という素数の発見方法なのです。それは、数表を使った方法でした。数表とは、下のような数の表です。

表の右上から右に向かって1から順番に数字が書かれてあります。ここでは、100までを書きました。

では、この表を使って素数を見つけていきましょう。100までの中の素数を見つけていきます。

倍数を消していこう

まず、素数の定義より1は素数ではないですので表から1を消します。

次に、2に進みます。2は1と自分以外の数で割り切れる数は持たないため素数です。

ですので、2は残しますが、2の倍数を表から全て削除します。これが2による”ふるい”です。

偶数を消すだけなので簡単ですね。上の表のように縦に線を五本いれるだけです。

続いて3です。3も素数ですのでそのままにして、その他も3の倍数を消します。これが3による”ふるい”です。

これも斜めに線を入れるだけであるので簡単ですね。

続いては4ですが、これは2を考えたときに消しました。なので、飛ばして5にいきましょう。

5に対してもどうように5以外の5の倍数を消します。

このように、5の後も繰り返していきます。

どこまで調べればいいの？

この操作をどこまで繰り返していけばいいのか。それは、調べている数の最大値を\(n\)とすれば、

$$\sqrt{n}$$

までです。

今の場合は、100までの数の素数を調べようとしていますので、

$$\sqrt{100} = 10$$

までの数について倍数を消していけばよいです。

これが”エラトステネスのふるい”の素晴らしいところです。

通常の方法では1～100までを一ずつ調べ素数かどうかを判定していく必要がありましたが、その1/10の1～10までを調べればよいのですから、大幅な計算量の削減に成功しています。

1～10までといっても実際は、2を考えたときに4が消えたように、考えないでいい数も多く出てきますので、もっともっと計算は簡単になります。

1～100までを考えた今の場合は、

$$2, 3, 5, 7$$

の四つについて”ふるい”を行えばよいということになります。

 

最終的な数表は以下のようになります。

青丸で示した数字が残った数であり、素数です。

1～100までの数には、素数は25個あることが分かりました。

 

今回は100までの素数を見つけましたが、この”エラトステネスのふるい”を使った方法なら1000までの素数も頑張ればできそうですよね。

\(\sqrt{10000}=100\)ですので、100までの数について”ふるい”にかければよいのです。

 

スポンサーリンク

まとめ

• ”エラトステネスのふるい”を使えば効率よく素数を見つけることができる
• 2から順にその数の倍数を消していく
• 調べたい数の最大の数\(n\)の\(\sqrt{n}\)まで2の操作を繰り返す
• 最終的に残った数字が素数である