天才数学者カール・フリードリヒ・ガウスの逸話
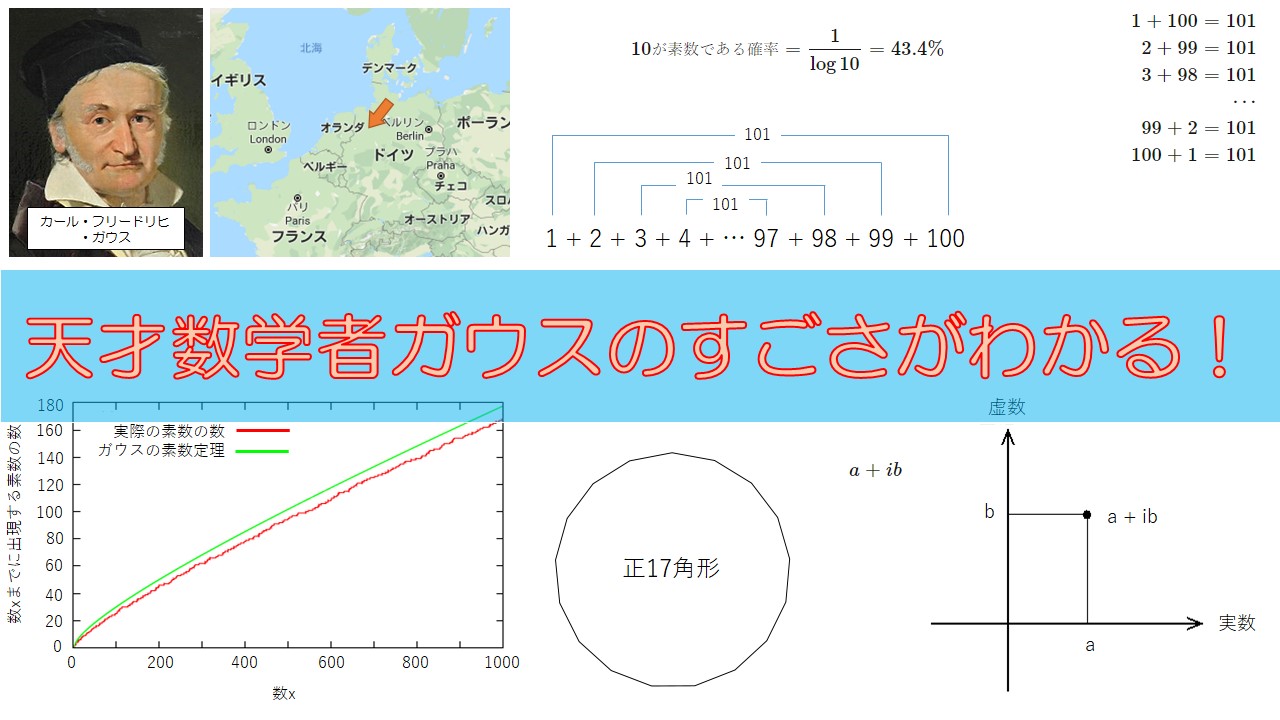
”ガウス”こと、フルネームを「カール・フリードリヒ・ガウス」は数多くの数学者の中で、もっとも偉大な数学者であると位置づける人も多いです。
ここでは、その天才ぶりを数々の業績と逸話をまじえて紹介していきましょう。
数々の逸話が残る天才数学者カール・フリードリヒ・ガウス
ドイツの数学者、天文学者、物理学者であるカール・フリードリヒ・ガウスは、「数学者の王子」と「歴史上最高の数学者」と呼ばれています。
彼は、現代の数学や科学など多くの分野に著しい影響を与えていることから、歴史上最も影響力のある数学者の一人として位置づけられています。
ガウスは幼少期から天才と呼ばれていました。
彼は非常に早くから数学の才能を発揮し、十代の頃に数学の分野で重大な発見をしますが、もっと幼いころから多くの逸話を残しています。
例えば、彼がちょうど3歳になった頃に、父親の給料の計算の誤りを指摘したと言われています。
5歳になった時には、父親の代わりに口座を定期的にチェックしていました。
スポンサーリンク
小学校の先生を驚かせたガウスの計算センス
そして、ガウスの逸話の中でもっとも有名なのが、7歳のときに算数で小学校の教師を驚かせたことです。
算数の教師は小学校のクラスの生徒に、
「\(1\)から\(100\)までの整数をすべて足しなさい」
といいました。
その教師は、この計算が終わるのは一番早い生徒でも10分以上かかるだろうと予想していました。
しかし、ガウスはこの問題を、一瞬で解いてしまったのです。
その方法は、以下のようなものでした。
$$1+2+3+4+\cdots+98+99+100=$$
を計算するに、まず\(1\)と\(100\)を足します。すると、
$$1+100=101$$
です。
続いて、\(2\)と\(99\)を足します。
$$2+99=101$$
さらに、
\(3\)と\(98\)を足すと、
$$3+98=101$$
ですね。
その後も同じように、計算を続けていきます。
\begin{align}
1+100=101 \\
2+99=101 \\
3+98=101 \\
\cdots \\
99+2=101 \\
100+1=101
\end{align}
このように、\(1\)から\(100\)までの数を外側から順に足していったのです。
足す数は100の半分の50ということが分かるので、101を50回足すということは、
$$101 \times 50 = 5050$$
です。
当時のガウス少年には、この掛け算を暗算することはたやすいことだったでしょう。
わずか7歳でこのような計算方法を一瞬で思いつき、瞬時に答えを導いたガウスはやはり天才としかいいようがありませんね。
その後のガウス少年
ガウスが生まれた家庭は貧しく、貴族階級とは程遠い労働階級でしたが、ガウスのスバ抜けた知的能力が、ブランズウィック公爵の目にとまります。
ブランズウィック公爵は彼の才能を認め、15歳のガウスをブラウンシュヴァイク工科大学に入学させました。
そして、その後も1795年から1798年にかけて有名なゲッティンゲン大学に通わせてくれます。
ガウスはこの時代にいくつかの重要な定理を発見しています。
素数の出現パターンの発見
ガウスが15歳で発見した重要な定理の一つが、素数が現れるパターンについてです。
数学の歴史において、素数は古くから研究されているテーマです。
数学者たちは1から順番に数を数えていったとき、素数は完全にランダムにあわられることを知っていました。
そこで、ガウスは少し変わった観点からこの素数を研究しました。
ガウスは数が増えるにつれて、素数の出現頻度が減少しておくことに気づきました。
そして、それを以下のようなグラフを描きました。
横軸に数\(x\)をとり、縦軸にはその数\(x\)までに何個の素数が存在しているかを描いたものです。
赤い曲線は実際の素数の数ですが、数が増えるをだんだんと傾きが緩やかになっています。
これは
数が大きくなるほど、素数が見つかりにくくなってくる
ということです。
ガウスは、ランダムにある数を選んだときに、その数が素数である確率は、以下の式で表現できるとしました。
$$\text{任意の数\(x\)が素数である確率} = \frac{1}{\log{x}}$$
この式は”ガウスの素数定理”と呼ばれています。
例えば、任意の数が10だったとすると、その数が素数である確率は、
$$\text{\(10\)が素数である確率} = \frac{1}{\log{10}} = 43.4\%$$
となります。※\(10\)は素数ではないことがわかっていますが、本来はもっと大きな数（素数かどうかわからない数）に対して、この定理が使われます。
この定理を上のグラフに描いたのが、黄緑の線です。
若干、ガウスの素数定理の方が大きいですが、おおよそ特徴などは一致していますね。
もう一度言いますが、ガウスがこれを発見したのが10代の頃なのです。
しかし、ガウスはこの発見を生涯の後半まで秘密にしていました。
それは、上のグラフからもわかるように、素数の数を近似的にしか表現していないからだったと言われています。
ガウス自身はもっと完璧に素数の数を表現できる式を見つけてから世の中に発表したかったのかもしれません。
ガウス、19歳で数学の歴史を変える
1796年、ガウスが19歳のこの年は、”驚異の年”と言われており、数学の歴史上まだ誰も成し遂げていなかったことを成功させました。
それは、
定規とコンパスだけで正17角形を描く
ということです。
これは数学の歴史で多くの数学者が挑戦し、断念してきたことだったのです。
そんな難問をガウスは19歳という若さで成し遂げてしまいました。
ガウスは数学のほとんど分野で偉大な功績を残しましたが、その中でも整数論は特に彼が好んで取り組んだ分野でした。
彼の有名な言葉に、
「数学は科学の女王であり、整数論は数学の女王である」
という名言があります。
彼は生涯にわたって整数論を研究し、複素数（実際に存在する数と実際には存在しない数を組み合わせて作る数）の研究にも大きな功績を残しました。
ガウスは複素数について明確な解説をお混って、複素数の変数に対して詳しい研究を行った初めの人物です。
複素数はガウスが登場する約200年前の16世紀初頭から、通常の数（実数）を使った方法では解けなかった方程式を解くために使用されていました。
あのガウスに唯一対抗できると言われている、もう一人の天才数学者レオンハルト・オイラーもガウスの少し前（18世紀）に複素数の分野を研究しています。
しかし、ガウスが登場するまでは、実数にどのように虚数が結びついているかの明確なイメージはありませんでした。
ガウスの複素数に対する功績の一つに、複素数を、
$$a + ib$$
と表現したことが挙げられます。
この表記は現代も受け継がれ、使用されています。
ガウスについても偉大な業績や逸話はまだまだ書ききれないほどにありますが、今回はこのあたりで終わります。
また、機会があれば続きを書いていこうと思います。
ちなみに、私が独断で選んだ天才数学者ランキングではガウスは第2位としています。
さて、第1位はだれでしょうか？興味のある方は、以下の記事をどうぞ。
https://analytics-notty.tech/ranking-of-genius-mathematician/スポンサーリンク
まとめ
- ガウスは幼いときから、すでにその才能を発揮していた
- 小学生のとき、1から100までのすべての数を足すという課題を一瞬で解き、先生を驚かせた逸話は有名
- 数学・物理学・天文学とすべての分野で偉大な業績を残してきた天才中の天才
- 特に数学の整数論を好み、「数学は科学の女王であり、整数論は数学の女王である」という名言を生んだ
- ここでは書ききれなかったほど、まだまだ業績や逸話が存在する