142857 – 答えが循環する不思議な数字

2018年1月18日2020年5月21日

一見何の規則性もない数字”142857″が…

“142857”という一見何の規則性もない数字が、ある面白い法則をもっています。

実は、この数字”142857″は循環する数として知られているのです。

“142857”のもつ様々な不思議な現象を紹介しましょう。

 

スポンサーリンク

“142857”に一桁の数字を掛けると…

“142857”に一桁の数字を掛けてみましょう。1から6までの数を掛けた値を下に示します。

\begin{align}
142857 \times 1 & = 142857 \\
142857 \times 2 & = 285714 \\
142857 \times 3 & = 428571 \\
142857 \times 4 & = 571428 \\
142857 \times 5 & = 714285 \\
142857 \times 6 & = 857142
\end{align}

答えを見てみましょう。一見、何の規則性もなさそうですが、良く見るとすべて同じ数字、同じ順番で数字が並んでいます。数字が循環しているのです。

違うのは、どの数字から始まっているかですね。

わかりにくい場合は、”1″がどの位置から始まっているかを探せばよいでしょう。

 

例えば、当然1を掛けた場合の答えは”142857″であり、次に5を掛けた場合は一つだけ1の位置が右にずれて”714285″となっています。

さらに1が右に一つずれたものが掛ける4の場合ですね。

これを分かりやすいように、並び替えてみましょう。すると、

\begin{align}
142857 \times 1 & = 142857 \\
142857 \times 5 & = 714285 \\
142857 \times 4 & = 571428 \\
142857 \times 6 & = 857142 \\
142857 \times 2 & = 285714 \\
142857 \times 3 & = 428571
\end{align}

となります。下の図のように、数字がどんどん右下にずれていっているのがわかりますか？

このように、”142857″に一桁の数を掛けることで数字が循環する答えを作ることができます。

このような数字のことを巡回数（じゅんかいすう）と呼ぶようです。

巡回数（じゅんかいすう、Cyclic Number）とは、2倍、3倍、4倍…と乗算したとき（あるいは同じ数を連続して加算したとき）に、その各桁の数を順序を崩さずに巡回させた数になる、整数のことである。ダイヤル数ともいう。
出典：巡回数：ウィキペディア（Wikipedia）

 

ここで、

「あれ？１～６までは掛けてるけど７以降は？」

と思いましたか？

 

では、7を掛けてみましょう。

すると、

$$142857 \times 7 = 999999$$

と9だけの答えとなるのです。これも美しいですね。

 

ちなみに、8と9を掛けた答えはこちらです↓

\begin{align}
142857 \times 8 & = 1142856 \\
142857 \times 9 & = 1285713
\end{align}

う～ん、これは何の特徴もなさそうですね。少なくとも私にはそう見えました。

「この数字にこんな規則があるんだ！」

という人は是非教えてください！

 

7と密接は関係がある”142857″

142857は”7″と密接な関係があります。まずは、1を7で割ってみてください。

$$1 \div 7 = 0.142857142857\cdots$$

答えの小数点以下の数字に注目です。なんと、”142857″の繰り返しになっています。

 

次に、2から6までの数を”7″で割った結果を示しましょう。

\begin{align}
1 \div 7 & = 0.142857142857\cdots \\
2 \div 7 & = 0.285714285714\cdots \\
3 \div 7 & = 0.428571428571\cdots \\
4 \div 7 & = 0.571428571428\cdots \\
5 \div 7 & = 0.714285714285\cdots \\
6 \div 7 & = 0.857142857142\cdots
\end{align}

こちらも数字が循環していることがわかると思います。またまたわかりやすいように並べ替えてみましょう。

\begin{align}
1 \div 7 & = 0.142857142857\cdots \\
5 \div 7 & = 0.714285714285\cdots \\
4 \div 7 & = 0.571428571428\cdots \\
6 \div 7 & = 0.857142857142\cdots \\
2 \div 7 & = 0.285714285714\cdots \\
3 \div 7 & = 0.428571428571\cdots
\end{align}

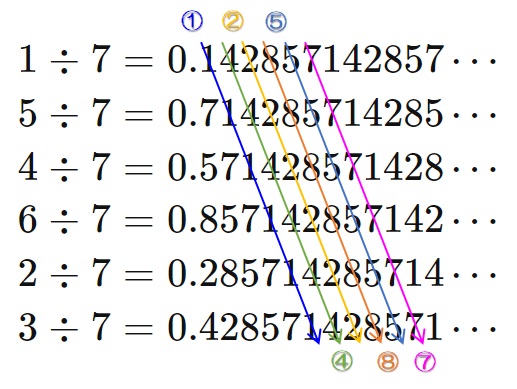
誰が見つけたんでしょうね。こんなこと。すごいです！

 

スポンサーリンク

9が連続した答えを作り出す

142857は”9″が連続した数を作り出すことも得意です。

すでに述べたように、142857に7を掛けると、

$$142857 \times 7 = 999999$$

となることを紹介しましたが、それ以外にも連続した9を作り出す方法があります。

 

まず、142857を二桁ずつに分けてください。

142857 → 14 | 28 | 57

そして、これらの分割した数を足します。

$$14 + 28 + 57 = 99$$

となり、99が出てきました。

 

三桁ずつに分けた場合もやってみましょう。

142857 → 142 | 857

これらの数を足します。

$$142 + 857 = 999$$

今度は9が三つ連続した答えが出てきました。

 

まとめると、

\begin{align}
142857 \times 7 & = 999999 \\
14 + 28 + 57 & = 99 \\
142 + 857 & = 999
\end{align}

となります。

９という数字とすごく相性がいいのですね。

 

ちなみに、９という数字も実はすごく特別な数字なんです。興味のある人は以下の記事も見てみてください。きっとビックリしますよ！

 

同じ数に戻ってくる性質を持つ

最後に、同じ数に戻ってくる面白い性質を紹介します。

まず、142857を二乗してください。

$$142857^2 =142857 \times 142857 = 20408122449$$

となります。※これは桁が多すぎて通常の電卓では計算できないかもしれません。私はGoogleの電卓を使って計算しました↓

 

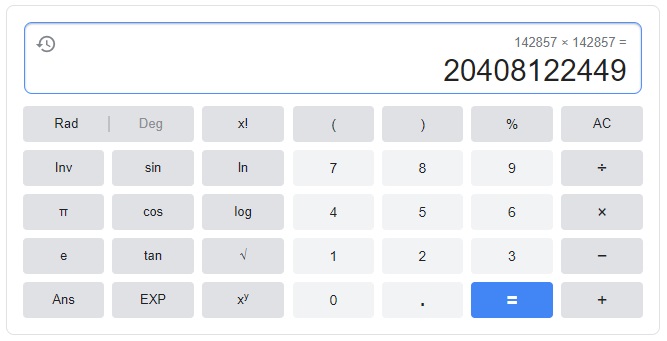
出てきた答え”20408122449″を左5桁と右6桁に分解します。

20408122449 → 20408 | 122449

そして、この二つの数を足してみましょう。

$$20408 + 122449 =142857$$

なんと、142857へ戻ってきました。これはなんとも不思議ですね。

 

元に戻ってくる性質を持つ数を”カプレカ数”と呼びます。

またこことは少し違った”カプレカ数”が持つ不思議な性質については、下の記事でも紹介していますので、興味のある方はどうぞ。

 

スポンサーリンク

まとめ

• “142857”に1～6までの数を掛けると、それらの答えは”142857″の循環になっている
• “142857”に7を掛けると、答えは999999となる
• 1～6までの数を7で割ると、それらの答えは”142857″の循環になっている
• “142857”は色々な方法で連続した9を作り出すことができる