素数の不思議 – 素数の魅力を紹介しています!
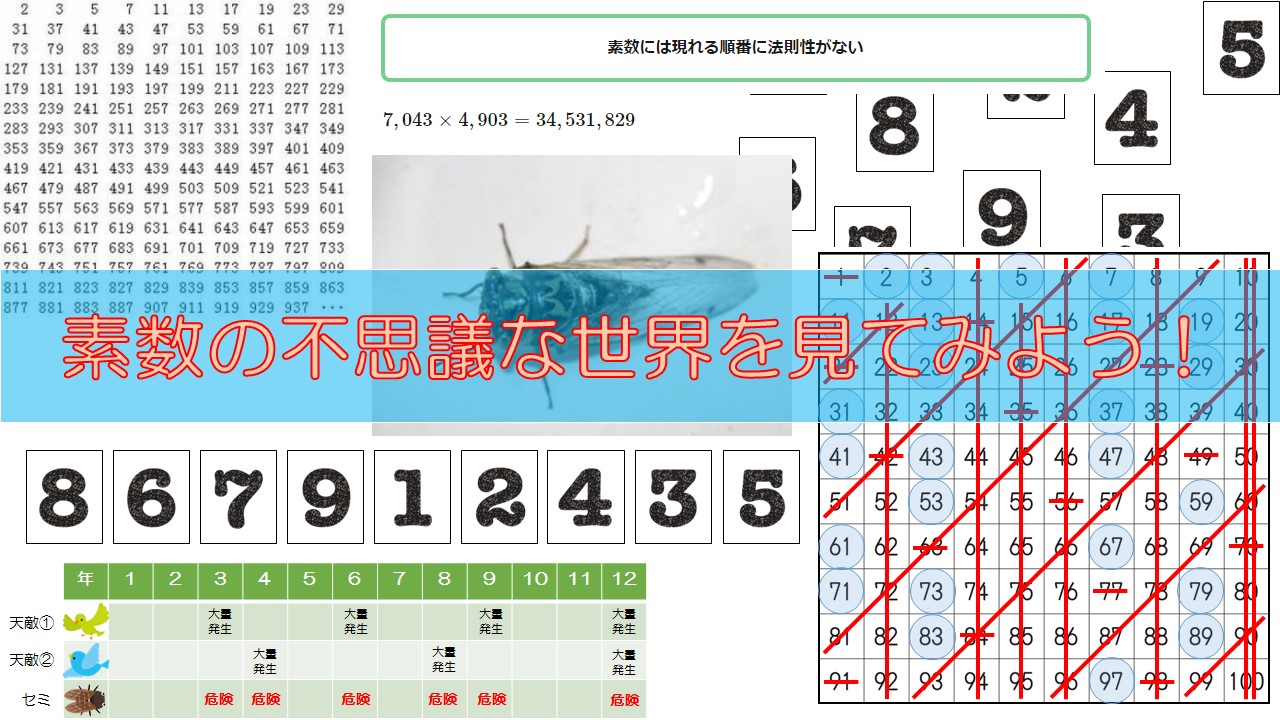
素数には不思議なことがたくさんあります。
自然界には生存競争を勝ち抜くために、素数を使っている生物が多くいます。
まだまだわかっていないことも多いです。そんな素数の分からない部分を逆に利用して、我々の情報を守るセキュリティシステムに利用されていたりもします。
そんな不思議で面白い素数の世界を紹介しましょう。
素数の簡単な復習
はじめに少しだけ素数とはどんな数字であるかを復習しておきましょう。
素数とは、
\(2\)以上の整数のうち、\(1\)と自分自身でしか割り切ることができない数
のことです。

例えば、\(7\)は素数です。
その理由は、”\(7\)は\(1\)と自分自身(\(7\))でしか割り切ることができない”からです。
その他にも、素数には、
$$2, 3, 5, 7, 11, 13, 17, 19, 31$$
などがあります。
スポンサーリンク
素数の不思議①:現れる順番に法則性がない
上で紹介した素数のように、1桁やせいぜい2桁程度の数であれば、その数が簡単に素数であるかどうは判断できるでしょう。
しかし、もっと桁数が大きい数字を素数どうか判断するのはかなり至難のわざです。
例えば、以下の数は素数でしょうか?考えてみましょう。
$$119$$
一見、素数のようにも思えますが、\(119\)は素数ではありません。
この数は\(7\)と\(17\)で割り切れるのです。
\begin{align}
119 \div 7 = 17 \\
119 \div 17 = 7
\end{align}
このように、素数であるかどうかの判断は難しいものです。
素数であるかどうかの判断が難しければ、素数を求める式を作ってしまえばよいのではないでしょうか?
例えば、\(3\)の倍数を見つけ出すには、\(3\)の倍数の式、
$$\text{\(3\)の倍数} = 3 \times n, \quad n=1, 2, \cdots$$
という式を使えば、\(n\)に適当な数を入れるだけで\(3\)の倍数ができてしまします。
こんな式を素数に対しても作ればよいのです。
しかし、これが作れないです。その理由は、
素数には現れる順番に法則性がない
からです。
先ほど例に出した\(3\)の倍数の式であれば、\(9\)の次に三の倍数になるのは、\(12\)であることがすぐに分かります。
これは、”いまの数に\(3\)を足すと次の目的の数になる”という法則があるからです。
しかし、素数には”いまの数に何か操作(足したり掛けたり)をして次の数にする”ということができないのです。これは素数が現れる順番に法則性が無いからです。
もしかすると、私たちが法則性に気づいていないだけかもしれませんが、過去の偉人たちや現代のテクノロジーをもってしても未だに見つけられていません。
以下の記事では、過去の天才達が素数の法則を見つけようとした努力の航跡を紹介しています。
素数の不思議②:素数を効率的に見つける方法はあるが…
上で見てきた通り、素数を見つけるのは至難の業(わざ)です。
法則性が見つからない限り、手あたり次第にその数が割れるかどうかを判断する必要があるからです。
ただ、その中でも効率的に素数を見つける方法も考え出されました。
それが”エラトステネスの篩(ふるい)”という方法です。この方法は簡単に言ってしまうと、消去法です。
まず、調べたいすべての整数を一覧表にします。以下のような表ですね。
一覧表ができたら、最初は\(2\)の倍数を消します。ただし、\(2\)自体は残しておきます。
次に\(3\)の倍数を消します。ここでも\(3\)自体は残してください。
次は\(4\)ですが、これはもう消えていますので飛ばします。
さらに、\(5\)の倍数を消します…というふうに次々に素数の倍数を消していけば最後には素数だけが一覧表に残るのです。以下の表が完成したものです。
これが”エラトステネスの篩”です。
上の操作に加えて、どの段階で倍数を消す作業をやめるかといった細かいルールがありますので、詳しく知りたい人は以下の記事をご覧ください。
この方法は古代ギリシャのエラトステネスというっ数学者によって考案されました。
今から2000年以上前の時代です(紀元前276年~紀元前194年)。
そして、2000年たった現在でも、エラトステネスの篩に勝る方法は見つかっていません。
コンピュータを使って素数だけを抜き出す場合でも、基本的には、素数の倍数を消していくという計算を行っているだけなのです。
このように、素数を見つけ出すのはものすごく難しいのです。
しかし逆に、この見つけにくさが、私たちのメールやデータの情報を守るための暗号化に役立っています。
例えば、\(34,531,829\)は二つの素数を掛けたものですが、その二つの素数を見つけ出すのはコンピュータを使わないとほとんど不可能でしょう。
答えは、
$$7,043 \text{と} 4,903$$
です。
上の例では”素数同士を掛け合わせた数”として、\(34,531,829\)を例に出しましたが、もっともっと大きな素数になると、コンピュータでもほとんど不可能になります。
逆に、この二つの数から\(34,531,829\)を導き出すのは比較的簡単です。
$$7,043 \times 4,903 = 34,531,829$$
頑張れば手計算でも計算できそうですね。
このように、”素数”から”素数同士を掛け合わせた数”は簡単に求まります。
逆に、”素数同士を掛け合わせた数”から”素数”を見つけ出すのは難しいのです。
\begin{align}
\text{素数} \rightarrow \text{素数同士を掛け合わせた数} : 簡単 \\
\text{素数同士を掛け合わせた数} \rightarrow \text{素数} : 難しい
\end{align}
このことを利用して現代の暗号化は行われています。
詳しくは以下の記事でご覧ください。
スポンサーリンク
素数の不思議③:素数を使って生き残る”素数ゼミ”
日本にも生息している”セミ”は、十数年間、幼虫として地中で暮らし、最後の数日間だけ地上に出て成虫として暮らす昆虫です。

地中にいた幼虫が地上に出てきて成虫になることを羽化といいます。
アメリカには、羽化の周期が正確に13年や17年ごとであるセミが生息しているのです。
13と17は素数ですので、これらのセミのことを”素数ゼミ”と呼んでいます。
13年ごとに羽化するのは主にアメリカの南部に生息する素数ゼミ、17年ごとに羽化するのは北部に生息する素数ゼミです。
素数ゼミの羽化する周期が13年や17年と素数なのは、単なる偶然ではありません。
これには彼ら素数ゼミが生き残るために選んだ戦略の一つなのです。
その理由は、
素数の倍数で羽化することにより、
- 天敵が大量発生する周期となるべく一致しないようにする
- 他の種類のセミの周期と一致しないようにすることで、異なる種との交配を避け、種の保存を守る
ためと考えられています。
つまり、天敵や別のセミの周期的な大量発生をできるだけ避けているのです。
これは、
素数を使って、ほかの数との最小公約数をできるだけ大きくしている
という言い方もできます。
素数が人間だけでなく、自然界でも使われているとは面白いですね。
詳しい説明は以下の記事をご覧ください。素数ゼミの謎について解説しています。
素数の不思議④:数学的な素数の性質
ここでは、数学や数字としての素数の不思議な面を紹介していきましょう。
まずは、二つ問題形式で紹介します。まずは自分で考えてみてくださいね。
1~9までの数字を1回ずつ使って素数は作れる?
さっそく問題です。
ここに、1~9の数字が書かれたカードが1枚ずつ、合計9枚あります。

これらのカードを自由に並び替えて9桁の整数を作ります。

その数が素数になるように並べることはできるでしょうか?
そのまま考えるのは難しいので、ヒントをお教えしましょう。
各桁の数字を足し算して作った整数が\(3\)で割り切れるとき、元の整数も\(3\)で割り切ることができる
です。
例えば、\(3621\)という数字があったとします。
この数の各桁の数字をすべて足すと、
$$3 + 6 + 2 + 1 = 12$$
ですね。\(12\)は\(3\)で割り切れる数です。
したがって、元の数の\(3621\)も\(3\)で割り切れる数ということが分かります。
答えです。
答えは、”作ることができない”です。
その理由は、1~9までの数を一回ずつ使ってできる数は、各桁の数を足したら必ず、
$$1+2+3+4+5+6+7+8+9=45$$
となります。どのように並べ替えてもこのことは変わりません。
\(45\)は\(3\)で割り切れる数なので、元の数も\(3\)で割り切れる数に必ずなるのです。
\(1\)と自分自身以外で割り切れる数は素数ではありませんから、素数を作ることはできないのです。
素数かどうかを判断してみよう
では次の問題です。
次の数字のうち素数でないものを探してみましょう。
- \(31\)
- \(331\)
- \(3331\)
- \(33331\)
- \(333331\)
- \(3333331\)
- \(33333331\)
- \(333333331\)
この中に一つだけ素数ではない数字が存在します。
それはどれでしょう?
どれも素数っぽい数ですよね。
でもこの中に一つだけ”素数もどき”がいるのです。見つけ出しましょう。
これもヒントなしでは難しいです。
ヒントは、”\(17\)で割り切れるかどうか”です。
電卓を使って探してみてくださいね。
答えです。
素数でない数字は、最後の”\(333333331\)”です。
この数字は、\(17\)で割り切れてしまいます。
$$333333331 \div 17 = 19607843$$
他の数はすべて素数です。
この問題はヒントがないとかなり難しいでしょう。
このように、素数を探す作業というのは未だに効果的な方法が見つかっていないので難しいのです。※エラトステネスの篩(ふるい)くらいですが、これももの凄く効率的というわけではありません
特に、\(17\)や\(31\)など大きい素数の倍数は、人間の感覚では素数であるように見えてしまいます。
例えば、
- 119
- 341
などもパッと見は「素数かな?」と思いますがこれらは、素数ではありません。
まだまだ素数には不思議な性質がいっぱいありますが、今回はこの辺りで終わりにしましょう。
スポンサーリンク
まとめ
- 素数にはたくさんの不思議な性質がある
- 素数は現れる順番に法則がない(見つかっていない)
- 素数を見つけるための効果的な方法は現在存在しない。唯一”エラトステネスの篩(ふるい)”があるが、2500年以上前の方法であり現在もこの方法を使って素数を見つけ出している。
- 素数を利用して生存競争を生き抜いているセミ”素数ゼミ”がいる。素数ゼミは素数の倍数の年に羽化し、天敵や他の種のセミと会うことをできるだけ避けている
- 素数の数学的な性質には分からないことがまだ多い































ディスカッション
コメント一覧
2を除く素数は、『モナドカード』の『でんぐり返し』で消し去れない『おっとり刀』(ひだり流れの刀模様)で終わる数のようだ。
奇数の素数は、両端に『おっとり刀』を持つ唯一の模様を持つ(DNA)
の数と模様の限定(見える化)でイメージできそうだ・・・
自然数は、[絵本][もろはのつるぎ]で・・・
素数というのは絶対値が1の整数と絶対値が自分自身の数で割りきれない数ですね。
341÷31=11
むじー