【高校数学（因数分解）】割り算を使った因数分解のやり方を丁寧に説明

2018年9月8日

まずは、整式の割り算をできるようになろう

割り算を使用した因数分解をマスターするには、まず整式の割り算をしっかり理解する必要があります。

整式の割り算さえできるようになれば、あとは簡単です。

 

割り切れる整式の計算

実際に問題を解いていきながら、整式の割り算を理解していきましょう。

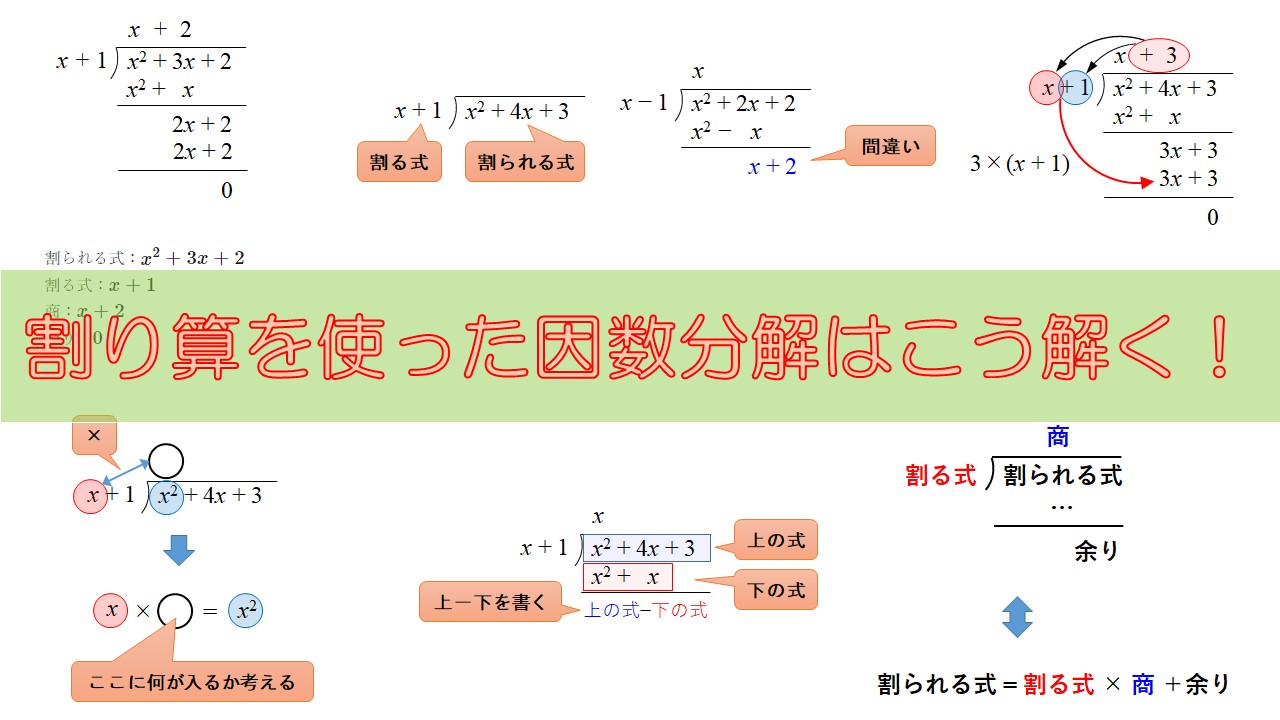
まず、下の図のように割られる式を右側、割る式を左側に配置します。

これは通常の割り算を筆算するときの形と同じですね。

 

次に、下の図で黒丸がついている箇所と\(x\)（赤丸）を掛け算をした時に\(x^2\)（青丸）となるには、何をかければ良いかえを考えましょう。

$$\bigcirc \times x = x^2$$

〇には\(x\)を入れればよいことがわりますね。

 

よって、以下のようになります。

 

上の図の赤い\(x\)がわかったので、この\(x\)を割る式\((x+1)\)の\(x\)と\(+1\)に掛け算して下の図の矢印の場所に計算結果を書きましょう。

 

書けたら上の式と下の式ができますよね。

(上の式)-(下の式)をして、その結果を棒線の下に書きましょう。

\begin{align}
& \text{上の式：} x^2+4x+3 \\
& \text{下の式：} x^2+x
\end{align}

ですので、(上の式)-(下の式)は、

$$(x^2 +4x+3)-(x^2 +x)=3x+3$$

となります。

 

この\(3x+3\)を棒線の下に書きましょう。すると、下の図のようになります。

 

さらに、同じ操作を割られる数の\(+4x\)についても行っていきます。

今度は下の図の黒丸がついている箇所と\(x\)（赤丸）が掛け算をした時に\(3x\)（青丸）となるには、何を掛ければ良いか考えます。

 

$$\bigcirc \times x = 3x$$

を成り立たせるには〇に3を入れてあげれば良いですね。

 

よって図の黒丸の場所には\(+3\)が入ります。

 

あとは先ほどと同じように\(x \times 3\), \(3 \times 1\)を計算し結果を書き足しましょう。

ここまで出来たらあとは(上の式)-(下の式)を行うだけです（下の図）。

(上の式)-(下の式)は、

$$(3x+3)-(3x+3)=0$$

となりますので、この式はちょうど割り切れたということですね。

\((x^2 +4x+3)\)は\(x+1\)で割り切れる

 

最終目標はここから、因数分解の解を導くまでですが、とりあえず今はここまでにしておきます。

 

割り切れない整式の計算

因数分解の解を導く前にもう一問、別の割り算を考えましょう。

やることは、例題①と同じです。

まず割る式と割られる式に分けましょう。

\begin{align}
& \text{割る式：}x-1 \\
& \text{割られる式：}x^2 +2x+2
\end{align}

 

次に下の図で、黒丸がついている箇所と\(x\)（赤丸）を掛け算した時に\(x^2\)（青丸）となるには、\(x\)が〇に入れば良いですね。

よって、図の○には\(x\)が入ります。

 

次に、この\(x\)と割る式\(x-1\)をかけ算しましょう。その答えを下に書きます。

書けたら次の図のように(上の式)-(下の式)をしましょう。

すると、

$$(x^2 + 2x + 2) – (x^2 – x)=3x+2$$

となるので、

となります。

 

ここまで大丈夫でしょうか？

あとは同じ作業を繰り返しましょう。

下の図で、〇と\(x\)（赤丸）と掛け算をした時に\(3x\)（青丸）となるには、〇に3を入れれば良いですね。

よって、〇には\(+3\)が当てはまります。

\(3 \times (x-1)\)を計算して\(3x-3\)を下に書きます。

 

さらに、(上の式)-(下の式)をし、その結果を棒線の下に書きましょう。

ここでも、上の「よくある間違い」で示した点に注意してください。

\(2-(-3)\)なので最終的な余りは\(5\)になります。\(-1\)にならないよう注意しましょう。

 

例題①では余りが\(0\)になりました。つまり、余りなしですね。

一方、例題②では余りが\(5\)です。余りが出たということを覚えておきましょう。

 

この計算は、これ以上計算を行おうとしても、\(x\)と何を掛け算しても\(5\)にはならないですよね。

ですので、以上で計算は終わりです。

 

スポンサーリンク

因数分解を考えよう

さて，整式の割り算が終わったら、次は最終目的の因数分解です。

 

ここで覚えてほしい公式があります。それは、

$$\text{割られる式}=\text{割る式} \times \text{商} + \text{余り}$$

です。

 

文字だけだとわかりづらいので、図で覚えましょう！

位置関係は大丈夫でしょうか？しっかりと覚えましょう。

 

例題①を因数分解してみる

$$\text{割られる式}=\text{割る式} \times \text{商} + \text{余り}$$

の式を例題①に当てはめてみましょう。

\begin{align}
& \text{割られる式：} x^2 +4x+3 \\
& \text{割る式：} x+1 \\
& \text{商：} x+3 \\
& \text{余り：} 0
\end{align}

でしたので、これらを公式に当てはめます。

\begin{align}
\text{割られる式} & ＝ \text{割る式} \times \text{商} + \text{余り} \\
x^2+4x+3 & = (x+1)(x+3)+0 \\
& =(x+1)(x+3)
\end{align}

となり、因数分解できてきることがわかります。

 

よって、\(x^2+4x+3\)を因数分解すると、\((x+1)(x+3)\)ですね。

 

例題②を因数分解してみる

次に例題②についても同じように、

\begin{align}
& \text{割られる式：} x^2 +2x+2 \\
& \text{割る式：} x-1 \\
& \text{商：} x+3 \\
& \text{余り：} 5
\end{align}

を公式に当てはめてみましょう。

すると、

\begin{align}
\text{割られる式} & ＝ \text{割る式} \times \text{商} + \text{余り} \\
x^2+2x+2 & = (x-1)(x+3)+5 \\
\end{align}

 

となります。

余りがあったので、\(+5\)という余分なものがついてしまいましたね。

この状態では因数分解できたとは言えません。

 

整式の割り算と因数分解は深い関係があることが理解できましたでしょうか？

少し複雑ですが、高次方程式を因数分解するためにしっかりと理解しましょう！

 

因数分解の問題を解いてみよう

では、ここまで学んだことを使って因数分解の問題へチャレンジしましょう。

以下の問題を考えます。

問題の式を因数分解するには、この式を割れきることができる整式を探さなければいけないことを、ここまでで知りました。

この式を割り切る整式は、どんなものがあるでしょうか？

 

それを見つけるには、\(x^2+3x+2\)の\(x\)に値を入れてみればわかります。

例えば、\(x=-1\)を入れてみましょう。

すると、

\begin{align}
x^2+3x+2 &= (-1)^2+3(-1)+2 \\
& = 1-3+2 \\
& = 0
\end{align}

となります。

答えが\(0\)になりましたね。

このとき、\(x^2+3x+2\)は\((x+1)\)で割り切れるということがわかります。

 

このように、\(x\)に代入して答えが\(0\)になる値を\(a\)とすると、問題の式は\((x-a)\)で割り切れるのです。※符号に注意です

これを因数定理というのですが、詳しくは以下のページをご覧ください。

[ブログカード]

 

ここでは、問題の式（\(x^2+3x+2\)）は\(x+1\)で割り切れることがわかりました。

あとは、実際に割ってから、その答えを以下の公式に当てはめるだけでしたね。

$$\text{割られる式}=\text{割る式} \times \text{商} + \text{余り}$$

 

では、割ってみましょう。途中の計算は今回は省略します。

\begin{align}
& \text{割られる式：} x^2+3x+2 \\
& \text{割る式：} x+1 \\
& \text{商：} x+2 \\
& \text{余り：} 0
\end{align}

必ず、余りが\(0\)になるはずです。

ここが\(0\)以外になれば、何が計算間違いをしている可能性があるので、チェックしましょう。

 

最後に、これを公式に代入します。

\begin{align}
\text{割られる式} & ＝ \text{割る式} \times \text{商} + \text{余り} \\
x^2+3x+2 & = (x+1)(x+2)+0 \\
& = (x+1)(x+2) \\
\end{align}

 

これで、因数分解完成ですね。

$$x^2+3x+2 = (x+1)(x+2)$$

 

3乗が登場する割り算を使った因数分解を行う問題については、以下の記事を参考にしてください。

 

スポンサーリンク

まとめ

割り算を使った因数分解は少し複雑な操作が必要です。

一見難しく感じるかもしれませんが、やることを覚えれば簡単に感じるようになるでしょう。

反復して理解、練習を重ねましょう。

 

以下、重要なポイントをまとめて終わります。