\(x^2-y^2=(x+y)(x-y)\)は図形を使えば簡単に証明・理解できる

2018年1月16日2020年5月19日

\(x^2-y^2=(x+y)(x-y)\)について

$$x^2-y^2 = (x+y)(x-y)$$

という数学の公式を覚えていますか？この公式は中学校で習います。

”因数分解”というもので、左の式”\(x_2-y_2\)”を右の式”\((x+y)(x-y)\)”へ分解しているのですね。

”\(x\)の二乗から\(y\)の二乗を引いたもの”（左辺）は”\(x\)と\(y\)の足し算と引き算をして掛けたもの”（右辺）と等しいという式です。

 

わたしは中学生の頃、この公式は単に暗記していました。なぜこの公式が成り立つのかは考えたことがありませんでした。

実は、この公式は図形を利用すると、簡単に理解・証明できてしまうのです。その面白い方法を紹介しましょう。

 

スポンサーリンク

公式の図形を利用した証明

まずは、

$$x^2-y^2 = (x+y)(x-y)$$

の左辺、

$$x^2-y^2$$

に注目しましょう。

\(x\)の二乗と\(y\)の二乗が引き算されています。

”\(x\)の二乗”とは、言い換えれば”一辺が長さ\(x\)の正方形の面積”ということができます。同様に、”\(y\)の二乗”とは”一辺が長さ\(y\)の正方形の面積”です。

\begin{align}
x^2 & = \text{一辺の長さが$x$の正方形の面積} \\
y^2 & = \text{一辺の長さが$y$の正方形の面積}
\end{align}

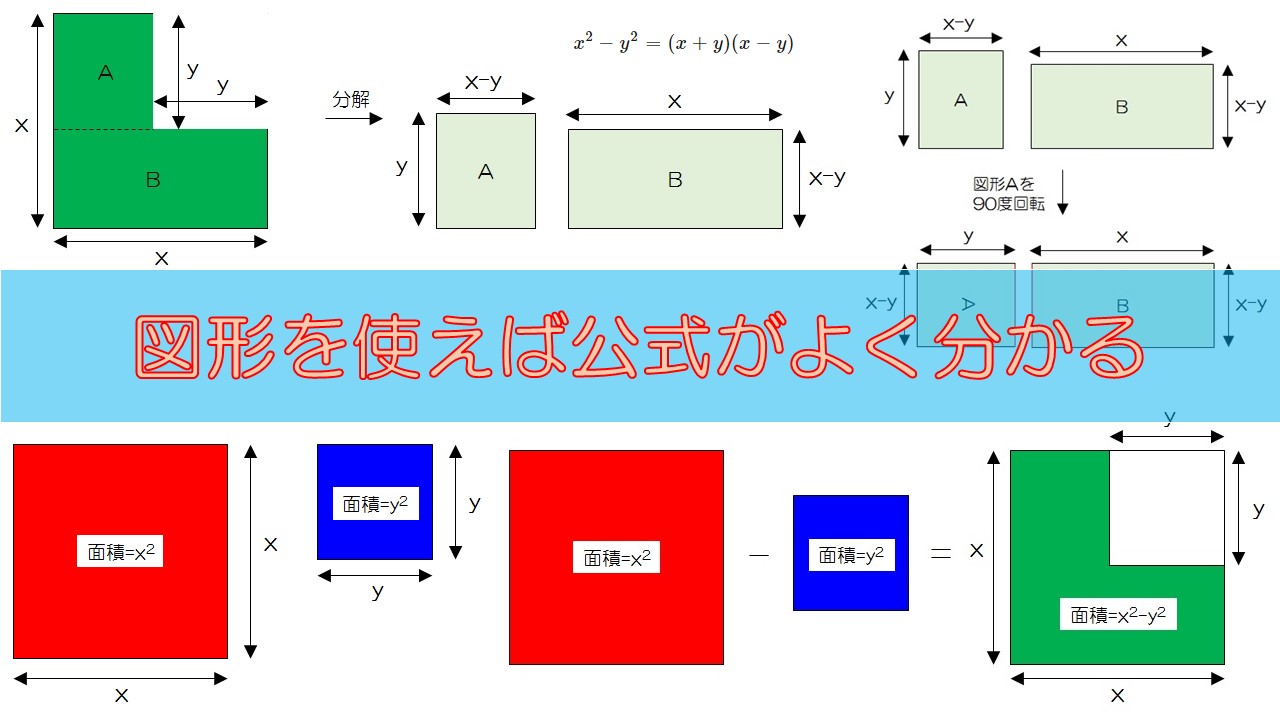
図に描くとこんな感じでですね。

ここで、”\(x_2-y_2\)”とは、”赤い正方形から青い正方形の面積を引いたもの”と理解することができますね。

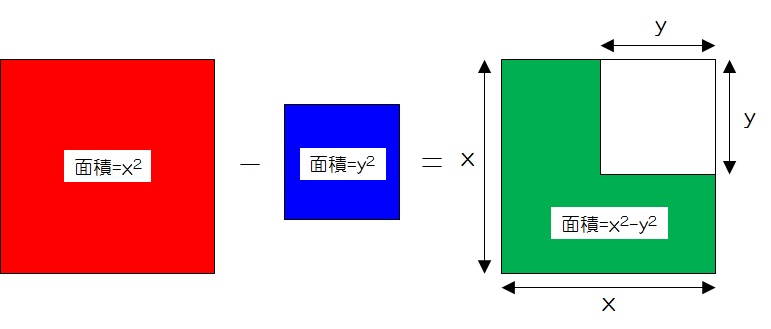
二つの正方形の面積を引き算したものは、緑の図形になります。緑の図形の右上の欠けた部分が青の正方形を引いた部分ですね。

ここで、緑の図形を二つの四角形に分解してみましょう。

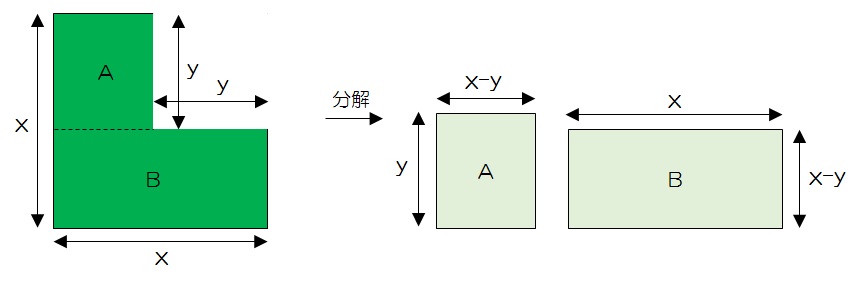
緑の図形を点線の部分から切り離し、図形AとBという二つの図形に分解しました。

各図形は長方形となり、長さはそれぞれ上の図に示している通りです。

 

次に、図形Aを90度回転させてみます。

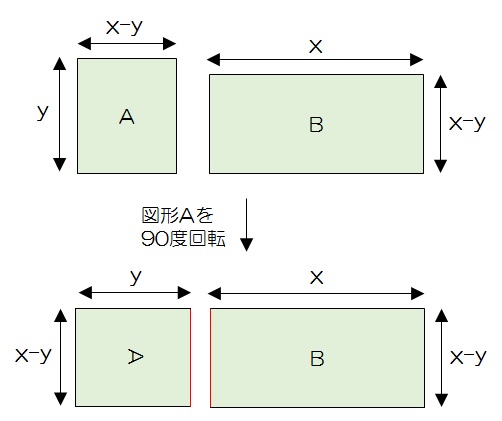
すると、二つの長方形の縦の長さが等しくなったことがわかります。その長さは、\(x-y\)です。

最後に、二つの長方形の図で示した赤いを辺をくっつけるようにして、結合させます。

すると、一つの長方形ができあがりました。

この長方形の横の長さは\(x+y\)、縦の長さは\(x-y\)です。したがって、面積は、

$$(x+y)(x-y)$$

となります。

ここで思い出して欲しいのですが、もともとこの図形は、

$$x^2-y^2$$

を切ったり、繋げたりして作ったものでした（下の図）。

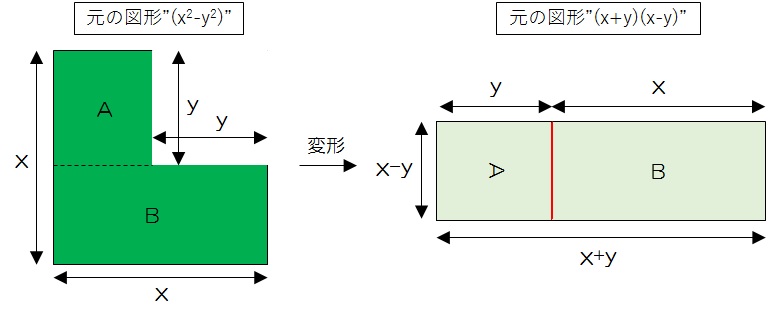
これで、

$$x^2-y^2 = (x+y)(x-y)$$

が証明できましたね。

 

数式をビジュアル化すること

公式をなんとなく覚えるだけよりも、このようにどうしてその公式が成り立つかを考えることは面白いですね。公式を忘れにくくもなります。

数式は、そのままではイメージしづらいものです。しかし、ここで紹介したように、図形を使って表現することで、視覚的に数式を理解できるようになります。

すべての公式でこのような図形による分かりやすい証明があるわけではないですが、視覚的に数式にアプローチする思考は大切ではないかとわたしは思っています。

図形を使った公式の証明は以下のようなものもあります。興味のある方はご覧ください。

 

スポンサーリンク

まとめ

• \(x^2-y^2=(x+y)(x-y)\)は二つの図形を引くと考えることで証明できる
• 図形を使って公式を証明する方法は視覚化できるため理解しやすい
• 他にも図形を使った証明は多くある