数学の面白い公式8選 – 私が選んだ美しくて面白い公式を紹介します
数ある数学の公式の中で、面白く、そして美しい公式を紹介します。
面白い数学公式①：オイラー積の公式
\begin{align}
\sum_n \frac{1}{n^s} & = \prod_p \frac{1}{1-\frac{1}{p^s}} \\
\\
n & = 1, 2, 3, \cdots \\
p & = 2, 3, 5, 7, 11, 13, 17, \cdots \\
s & = \text{\(2\)以上の任意の自然数}
\end{align}
左辺はリーマンのゼータ関数と呼ばれるもので、自然数\(n\)を使った形となっています。
一方、右辺は素数\(p\)についての関数となっており、オイラー積の公式は自然数と素数の関係をつなぐ式となっているのです。
例えば、\(s=2\)の場合について、\(\sum\)と\(\prod\)を使わずに書き直すと、
\begin{align}
\frac{1}{1^2}+\frac{1}{2^2}&+\frac{1}{3^2}+\cdots = \\
&\left( \frac{1}{1-\frac{1}{2^2}} \right)\left( \frac{1}{1-\frac{1}{3^2}} \right)\left( \frac{1}{1-\frac{1}{5^2}} \right)\left( \frac{1}{1-\frac{1}{7^2}} \right)\left( \frac{1}{1-\frac{1}{11^2}} \right)\cdots
\end{align}
となります。
きれいな数式ですね…
スポンサーリンク
面白い数学公式②：オイラーの等式
\begin{align}
e^{i\pi} + 1 & = 0 \\
\\
e & = \text{ネイピア数} \\
\pi & = \text{円周率} \\
i & = \text{虚数単位}
\end{align}
オイラーの等式と呼ばれる公式です。多くの数学の公式の中で、オイラーの等式はもっとも美しい式であると言われています。
その理由は、数学には無くてなならないもっとも有名な定数である\(\pi\)と\(e\)を含み、さらに虚数単位\(i\)の三つをつなぐ式であるからです。
さらに、見ての通り非常にシンプルに表現されています。数学の世界ではシンプルであることこそ美しいとされています。
オイラーの等式は、オイラーの公式、
\begin{align}
e^{i\theta} = cos(\theta) + i \sin(\theta)
\end{align}
の\(\theta=\pi\)とした場合の等式となっています。
面白い数学公式③：フィボナッチ数列の一般項
\begin{align}
F(n) & = \frac{(\phi)^n – \left( -\frac{1}{\phi} \right)^n }{\sqrt{5}} \\
\\
\phi & = \frac{1+\sqrt{5}}{2}
\end{align}
フィボナッチ数列を表すことのできる数式です。
フィボナッチ数列とは、\((1, 1)\)から始まり、前の二つの数を足したものが次の数になるという決まりを持った数列です。
フィボナッチ数列は以下のようになります。
$$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, \cdots$$
例えば、\(34\)に注目してください。\(34\)の前の二つの数は\(13\)と\(21\)ですが、この二つの数を足すと、\(34\)になります。
$$13+21=34$$
このようにして、数字をどんどん並べていったものがフィボナッチ数列です。
このフィボナッチ数列を表すことのできる式が、ここで紹介したフィボナッチ数列の一般項です。
この式に\(n=1, 2, 3, \cdots\)を代入していきましょう。
| \(n\) | \(F(n)\) |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
ちゃんと、前の二つの数を足した数が続いていますね。
初めて私がこの式を見たとき、「整数だけで構成された数列を表すのに、なぜ式に\(\sqrt{5}\)なんて入っているんだろう？」と思いました。
なので、「本当にこの式でフィボナッチ数列が導けの？」と疑っていたのですが、実際計算してみると見事にフィボナッチ数列が現れ少し感動したのを覚えています。
フィボナッチ数列について詳しく知りたい方は、以下の記事がお勧めです。
https://analytics-notty.tech/fibonacci-and-goldenratio-in-sunflower/
https://analytics-notty.tech/fibonacci-and-spiral/スポンサーリンク
面白い数学公式④：バーゼル問題
\begin{align}
\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots = \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}
\end{align}
自然数の二乗を分母にとった分数をすべて足し合わせると、なんと円周率\(\pi\)が出てきます。
これは不思議で面白い式ですね。
バーゼル問題を証明したのは、あの天才数学者レオンハルト・オイラーです。
まったくこの人はどこまで凄いんだ。
面白い数学公式⑤：調和数（発散列）
\begin{align}
\frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots = \sum_{n=1}^\infty \frac{1}{n} = \infty
\end{align}
先ほどのバーゼル問題と関連して、調和数（発散列）を紹介しましょう。
これは、バーゼル問題の式と似ていますね。
バーゼル問題では、二乗した数を分母に持ってきていましたが、これは二乗はせずに分母に置き、すべての自然数に対して足していきます。
バーゼル問題の式では、円周率\(\pi\)が登場しましたが、調和数の場合は、無限大に発散してしまいます。
面白いのは、数列、
$$\frac{1}{n}$$
自体は\(n\)が無限大へ向かうと\(0\)に収束するにも関わらず、それを足した数は無限大に発散するという事実でしょう。
スポンサーリンク
面白い数学公式⑥：ガウス積分
$$\int^\infty_{-\infty} e^{-x^2} dx = \sqrt{\pi}$$
ガウス積分もしくはオイラー・ポアソン積分と呼ばれる積分の式です。
通常、\(e^{-x^2}\)は積分できないものです。
しかし、積分区間を\(-\infty\)から\(\infty\)にすることで積分が可能になり、その値は円周率\(\pi\)のルートとなります。
以下は\(\int^\infty_{-\infty} e^{-x^2} dx\)のイメージ図です。
引用元：
面白い数学公式⑦：三平方の定理（ピタゴラスの定理）
$$a^2+b^2=c^2$$
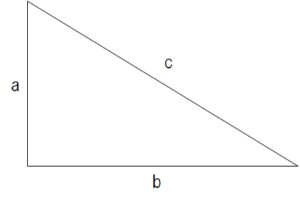
中学校で勉強する三平方の定理は、直角三角形の各辺の長さの関係を表した公式です。
シンプルにして美しい公式です。
この三平方の定理の証明方法は非常に多くあり、100種類以上あると言われています。
興味のある人は以下の記事をご覧ください。
https://analytics-notty.tech/proof-of-pythagoras-theorem-using-square/
https://analytics-notty.tech/proof-of-pythagoras-theorem-using-circle/
https://analytics-notty.tech/proof-pythagorean-theorem-with-puzzle/
面白い数学公式⑧：円周率と素数の美しい繋がり
\begin{align}
\frac{\pi^2}{6} & =
\prod_p \frac{1}{1-\frac{1}{p}} \\
\\
p & = 2, 3, 5, 7, 11, 13, 17, \cdots
\end{align}
左辺には円周率、右辺には素数を使った式であり、円周率と素数を美しく繋いだ面白い式です。
右辺の\(\prod\)は、\(\sum\)の掛け算バージョンであり、\(\prod\)の後に書いた式を掛け算します。
右辺を\(\prod\)を使わずに書くと、
\begin{align}
\frac{\pi^2}{6} & =
\left( \frac{1}{1-\frac{1}{2^2}} \right)\left( \frac{1}{1-\frac{1}{3^2}} \right)\left( \frac{1}{1-\frac{1}{5^2}} \right)\left( \frac{1}{1-\frac{1}{7^2}} \right)\left( \frac{1}{1-\frac{1}{11^2}} \right)\left( \frac{1}{1-\frac{1}{17^2}} \right)\cdots
\end{align}
となります。
これは、上で紹介したバーゼル問題の式とオイラー積を組み合わせた形になっています。
バーゼル問題では、円周率と自然数の関係を表した式でした。
一方、オイラー積は、自然数と素数の関係を表した式です。
この二つの式を使って、円周率と素数を繋いだ式がここで紹介した式だったのです。
この式の導き方は以下の記事で丁寧に解説しています。興味のある方はどうぞ。
https://analytics-notty.tech/relationship-between-pi-and-prime-numbers...
以上で終わりです。お疲れ様でした。
楽しんでいただけたでしょうか？数学の世界はなんとも面白くて美しいのでしょうか。
これを機にみなさんに数学を好きになってもらえるとうれしいです。
まとめ
- 数学の面白くて美しい式（公式）を8つ紹介した
- オイラー積の公式
- オイラーの等式
- フィボナッチ数列の一般項
- バーゼル問題
- 調和数（発散列）
- ガウス積分
- 三平方の定理（ピタゴラスの定理）
- 円周率と素数の美しい繋がり
- 結論、数学の世界は美しい