円周率と素数の関係 – 数の美しい繋がりをご覧ください

2018年3月12日2020年5月20日

円周率と素数は繋がっている

円周率とは、\(\pi \simeq 3.14\)という値で知られている数学の分野でもっとも有名な定数です。

円周率は元々、円の円周の長さと直径を結びつける数です。

円周の長さは直径の何倍か？

という値が円周率でしたね。

 

一方、素数とはまったく別の分野から生じたものです。素数は、

\(1\)と自分自身以外で割ることのできない\(1\)以外の数

のことです。

例えば、\(5\)や\(13\)は素数ですね。両方とも\(1\)か自分自身（\(5, 13\)）でしか割ることができません。

 

このように、円周率と素数はまったく無関係の考え方から生じた数字です。

しかし、数学の世界とは不思議なもので、この二つの数が繋がってしまうことがあるのです。

 

スポンサーリンク

出発点はゼータ関数

”円周率と素数の繋がり”までたどり着くためには、”ゼータ関数”を避けて通れません。※少なくとも私はそう思います

「ゼータ関数！難しそう…」

と思いましたか？

安心してください。すごく簡単です。

以下がゼータ関数です。

$$\zeta (x) = \frac{1}{1^x} + \frac{1}{2^x} + \frac{1}{3^x} + \frac{1}{4^x} + \frac{1}{5^x} + \cdots \frac{1}{n^x} + \cdots$$

分数をいくつも足し合わせていった数になってますね。

その分子は常に\(1\)ですが、分母の数は\(1\)から\(+1\)ずつ増えていってます。

そして、分母の数は何やら\(x\)乗されています。この\(x\)にはいろんな数が自由に入ります。

ゼータ関数とは\( 1 \sim \infty \)まで自然数を使った関数なのです。

 

余談ですが、このゼータ関数を最初に発見したのはレオハルト・オイラーという天才数学者でした。

私の独断と偏見のみで作った天才数学者ランキングでは、見事1位に輝いております。

 

ゼータ関数を計算してみよう

さて、このゼータ関数、

$$\zeta (x) = \frac{1}{1^x} + \frac{1}{2^x} + \frac{1}{3^x} + \frac{1}{4^x} + \frac{1}{5^x} + \cdots \frac{1}{n^x} + \cdots$$

の\(x\)に実際に値を代入してみましょう。

 

まずは、\(x=1\)を入れてみます。すると、

$$\zeta (1) = \frac{1}{1^1} + \frac{1}{2^1} + \frac{1}{3^1} + \frac{1}{4^1} + \frac{1}{5^1} + \cdots \frac{1}{n^1} + \cdots$$

となり、これを計算すると、※計算過程（証明）は省略します。

\begin{align}
\zeta (1) & = \frac{1}{1^1} + \frac{1}{2^1} + \frac{1}{3^1} + \frac{1}{4^1} + \frac{1}{5^1} + \cdots \frac{1}{n^1} + \cdots \\
& = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots \frac{1}{n} + \cdots \\
& = \infty
\end{align}

となり無限大になってしまいます。つまり、発散してしまうということですね。

 

では、次は\(x=2\)を入れてみましょう。すると、※またも計算過程は省略します（ちょっと難しいです）

\begin{align}
\zeta (2) & = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \cdots \frac{1}{n^2} + \cdots \\
& = \frac{1}{1} + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \cdots \frac{1}{n^2} + \cdots \\
& = \frac{\pi^2}{6}
\end{align}

なんとここで、円周率\(\pi\)が登場しました。

\(x=1\)のときは、発散しましたが、今回はちゃんと収束しました。

実は、\(x=2\)以上のときのゼータ関数は収束することが証明されており、\(x=4,6,\cdots\)など偶数のときに\(\pi\)が登場します。

\begin{align}
\zeta (2) & = \frac{\pi^2}{6} \\
\zeta (4) & = \frac{\pi^4}{90} \\
\zeta (6) & = \frac{\pi^6}{945} \\
\cdots
\end{align}

このように、自然数と円周率が繋がっていることがここで分かりました。

 

ゼータ関数から素数を導き出す

さて、ゼータ関数から円周率\(\pi\)が出てくるのは分かりましたが、まだ素数が登場していません。

ここでは、円周率と素数の関係を探しているのでしたね。

 

ゼータ関数の\(x=2\)の場合をもう一度みてみましょう。前よりも長く書いてみます。

\begin{align}
\zeta (2) & = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \frac{1}{7^2} + \frac{1}{8^2} + \cdots
\end{align}

これの分母の数を分解できるものは分解してしまいましょう。素因数分解です。

\begin{align}
\zeta (2) & = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{(2^2)^2} + \frac{1}{5^2} + \frac{1}{(2 \cdot 3)^2} + \frac{1}{7^2} + \frac{1}{(2^3)^2} + \cdots
\end{align}

分母が\(4\)、\(6\)、\(8\)だった項が素因数分解されていることに気づくと思います。

ここが少し難しいのですが、上の式は以下のように書き直すことができます。

\begin{align}
\zeta (2) & = \left( \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{(2^2)^2} + \frac{1}{(2^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{(3^2)^2} + \frac{1}{(3^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{5^2} + \frac{1}{(5^2)^2} + \frac{1}{(5^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{7^2} + \frac{1}{(7^2)^2} + \frac{1}{(7^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{11^2} + \frac{1}{(11^2)^2} + \frac{1}{(11^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{13^2} + \frac{1}{(13^2)^2} + \frac{1}{(13^3)^2} + \cdots \right) \\
& \cdots \\
& \cdots \\
& \cdots
\end{align}

分母に素数だけが使われた式になりました。ようやく素数の登場です。

素数は素因数分解によって登場したのですね。

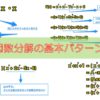
この式と元の式が同じであることを理解するには、以下のように考えてください。

例えば、元の式の、

$$\frac{1}{2^2}$$

の部分が、変形した式のどの部分かというと、

このように、緑で囲んだ部分を掛けたもので表すことができます。

もう一つ例を示すと、元の式の、

$$\frac{1}{(2 \cdot 3)^2}$$

の部分が、変形した式のどの部分かというと、

このように、青で囲んだ部分を掛けたもので表すことができます。

どうでしょうか？少し分かりにくいので、じっくりと考えてみてくださいね。

 

上の変形した式は、\(\prod\)を使って、

\begin{align}
\zeta (2) & = \left( \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{(2^2)^2} + \frac{1}{(2^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{(3^2)^2} + \frac{1}{(3^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{5^2} + \frac{1}{(5^2)^2} + \frac{1}{(5^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{7^2} + \frac{1}{(7^2)^2} + \frac{1}{(7^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{11^2} + \frac{1}{(11^2)^2} + \frac{1}{(11^3)^2} + \cdots \right) \\
& \times \left( \frac{1}{1^2} + \frac{1}{13^2} + \frac{1}{(13^2)^2} + \frac{1}{(13^3)^2} + \cdots \right) \\
& \cdots \\
& \cdots \\
& \cdots \\
& = \prod_{p;prime} \left( 1+\frac{1}{p^2}+\frac{1}{(p^2)^2}+\frac{1}{(p^3)^2}+\cdots \right)
\end{align}

と書けます。

\(\prod\)は、\(\sum\)の掛け算バージョンです。

なので、”\(\prod_{p;prime}\)は直後の括弧内の式の\(p\)を素数として掛けていく”という意味ですね。

もう一度書きます。

\begin{align}
\zeta (2) = \prod_{p;prime} \left( 1+\frac{1}{p^2}+\frac{1}{(p^2)^2}+\frac{1}{(p^3)^2}+\cdots \right)
\end{align}

ですね。これをオイラー積と言います。

 

スポンサーリンク

いよいよ円周率と素数が出会う

ここまででだいぶ疲れたかもしれませんが、あと一息です。

\begin{align}
\zeta (2) = \prod_{p;prime} \left( 1+\frac{1}{p^2}+\frac{1}{(p^2)^2}+\frac{1}{(p^3)^2}+\cdots \right)
\end{align}

の式の右辺の、

$$1+\frac{1}{p^2}+\frac{1}{(p^2)^2}+\frac{1}{(p^3)^2}+\cdots$$

を変形していきましょう。

まず、以下のように変形します。

\begin{align}
& 1+\frac{1}{p^2}+\frac{1}{(p^2)^2}+\frac{1}{(p^3)^2}+\cdots \\
= & 1+\left(\frac{1}{p^2}\right)+\left(\frac{1}{p^2}\right)^2+\left(\frac{1}{p^2}\right)^3+\cdots
\end{align}

ここで、\(r=1/p^2\)と置くと、

$$1+r+r^2+r^3+\cdots$$

となります。

ここで、高校数学で習う”べき乗の和の公式”

を使いましょう。

\(r\)は0と1の間をとる必要がありますが、ここでは、\(p\)は素数であり\(2\)以上なので、

$$r=\frac{1}{p^2}$$

は必ず(\(0 < r < 1\))となります。

 

これを使って、式を書き直すと、

\begin{align}
\zeta (2) & = \prod_{p;prime} \frac{1}{1-r} \\
& = \prod_{p;prime} \frac{1}{1-\frac{1}{p^2}}
\end{align}

となります。

ここで、\(\zeta (2)\)は、

$$\zeta (2) = \frac{\pi^2}{6}$$

であったことを思い出してください。

すると、最終的に、

\begin{align}
\frac{\pi^2}{6} & = \prod_{p;prime} \frac{1}{1-\frac{1}{p^2}} \\
& = \left(\frac{1}{1-\frac{1}{2^2}}\right) \left(\frac{1}{1-\frac{1}{3^2}}\right) \left(\frac{1}{1-\frac{1}{5^2}}\right) \left(\frac{1}{1-\frac{1}{7^2}}\right) \left(\frac{1}{1-\frac{1}{11^2}}\right) \cdots
\end{align}

となり、見事に円周率と素数がつながりましたね。

 

これで、円周率と素数が繋がっていることが分かりました。

しかし、ここまでの導出過程から分かるように、円周率と素数は直接繋がっているわけではなく、円周率が自然数と繋がっていて、自然数が素数と繋がっているのですね。

$$\text{円周率} \rightarrow \text{自然数} \rightarrow \text{素数}$$

 

まとめ

• 円周率と素数は自然数を介して繋がっている
• ゼータ関数が重要な関数となる