ベイズの定理とは – 初心者へ向けて分かりやすく解説します
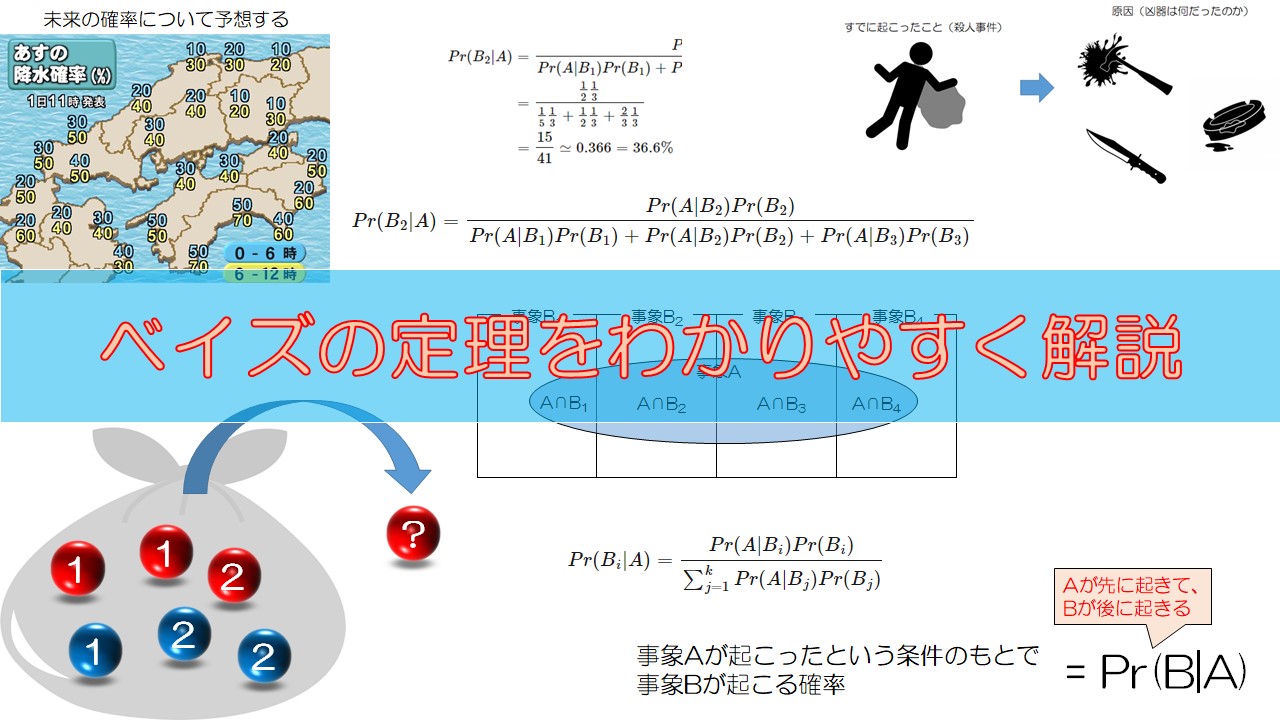
ベイズの定理を理解するために、一つひとつ順を追って、例題を交えながら解説していきます。一歩ずつ確実に理解しながら読み進めていってくださいね。
この記事を読み終わったときには、必ずベイズの定理を理解できているはずですよ。
ベイズの定理のイメージはこんな感じ
「ベイズの定理」は数学の確率の分野に属してしますが、普通の確率と少し違うポイントがあります。
まずは、その違いについてイメージを持つことからはじめましょう。
例えば、普段の生活で確率という言葉がよく登場するものの一つに天気予報があります。
「明日の降水確率は80%です。」
といったものです。
このように、日常生活で一般的な確率の概念は、
未来のことに対して、その事柄(事象)が起こる期待度を数値化したもの
です。ここで「未来のことに対して」というところがポイントです。

通常、確率は未来の予想に使うのが一般的ですね。
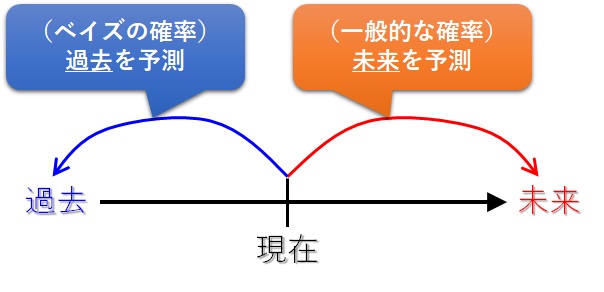
しかし、ベイズの定理では、時間軸が逆になります。次のような感じです。
ある事象が起こった。この事象が起きるような原因はいくつかあるが、これがその原因である確率は何パーセントである
のように、既に起こったことから過去の原因の確率を導いていくのがベイズの定理です。
つまり、言い換えると、
ベイズの定理とは、「結果」から「原因」を予測すること
となります。
現在すでに起こった結果から、それが起こった原因を推測するのですね。以下にその実例を紹介しましょう。
過去を予測する例
例えば、ある犯罪が起きたとします。それは以下のような殺人事件でした。
- 被害者は男性
- 犯行現場は被害者の庭
- 殺害方法は刺殺
- 犯行時刻は午後3時
容疑者は、A氏、B氏、C氏の三人です。
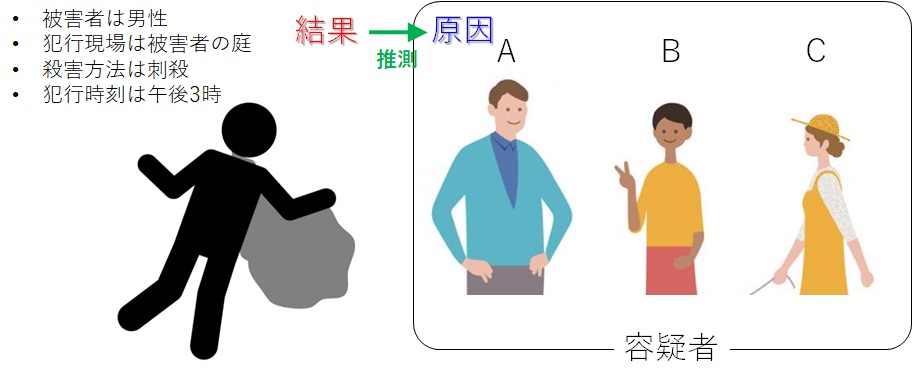
「このような手口の犯罪が発生したが、このような条件での殺害方法ははA氏の犯行である可能性が一番高い!」
といった感じです。
殺害状況という現在分かっている「結果」から、その「原因」である容疑者を探し出すのです。
ベイズの定理特有の、この時間軸の方向を常に意識しておくことが初学者にとってもっとも大切なことだと私は思っています。
私も理解するまでに、何度もこの基本概念に立ち返っては本を読み直していました。
では、以下からベイズの定理の理解へ向けて、必要なことを学んでいきましょう。
一つずつ確実に理解していけば、この記事を読み終わるときには、ベイズの定理とは何かを理解して、実際に使えるようになっているはずですよ!
スポンサーリンク
条件付き確率とは
まず、ベイズの定理を理解する上での第一歩として、”条件付き確率”を理解する必要があります。
条件付き確率とは、参考書などの説明によると、
”ある事象Aが起こったという条件のもとで、事象Bが起こる確率”
ということです。
しかし、初めて聞いた人はいまいちイメージが湧かないかもしれません。
実際に、例を使って説明しましょう。
いま袋の中に赤い玉と青い玉が三つずつ入っているとします。
さらに、玉にはそれぞれ1,2と番号が振ってあります。下の画像のような感じです。

赤い玉は(1,1,2)の三つが、青い玉には(1,2,2)の三つがあります。
この袋の中から一つの玉をランダムに取り出したところ、赤い玉でした。
この赤い玉の数字が1である確率はなんでしょう。
この場合の「一つの玉をランダムに取り出したところ、赤い玉でした。」というところが、条件付き確率の条件の部分です。
取り出した玉が赤い玉がであったという条件のもとで、数字が1である確率はなんでしょう
ということですね。
このように、”という条件のもとで”というフレーズが入るのが条件付き確率の特徴です。
このような条件付き確率を解くときには、以下の公式を使います。※この公式がなぜ成り立つかについては後ほど説明します。
$$Pr(B|A) = \frac{Pr(A \cap B)}{Pr(A)}$$
初学者には見慣れない記号ばかりだと思いますので、一つ一つ説明しましょう。
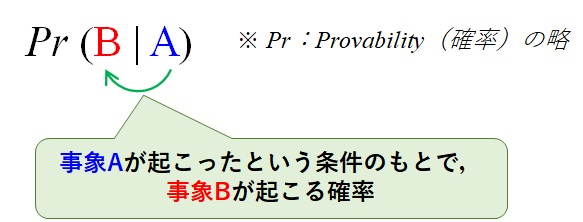
まず、\(Pr(B|A)\)は、
$$Pr(B|A) = \text{事象Aが起こったという条件のともで、事象Bが起こる確率}$$
を表現しています。
\(Pr(A)\)と\(Pr(A \cap B)\)は、
\begin{align}
Pr(A) & = \text{事象Aが起こる確率} \\
Pr(A \cap B) & = \text{事象Aと事象Bが同時起こる確率}
\end{align}
を表しています。
では、この公式を使って例題を解いてみましょう。事象Aと事象Bを以下のように考えます。
- 事象A:赤い玉を取り出した
- 事象B:番号は1であった
と置けば、\(Pr(B|A)\)は上記の定義により、
「赤い玉を取り出したときに、その玉の番号が1である確率」
となります。これはまさに今考えている問題で欲しい答えですね。
ですので、\(Pr(B|A)\)を上記の公式を使って求めていくことになります。
事象Aは「赤い玉を取り出した」ということです。これが起こる確率\(Pr(A)\)は、
$$Pr(A) = \frac{3}{6} = \frac{1}{2}$$
です。
次に、事象Aと事象Bが同時に起こるというのは、赤い玉でなおかつ数字が1の玉を取り出すということです。
よって、この確率\(Pr(A \cap B)\)は、
$$Pr(A \cap B) = \frac{2}{6} = \frac{1}{3}$$
ですね。
これで、\(Pr(A)\)と\(Pr(A \cap B)\)が分かりました。
これを、条件付き確率の公式、
$$Pr(B|A) = \frac{Pr(A \cap B)}{Pr(A)}$$
に代入すると、
\begin{align}
Pr(B|A) & = \frac{Pr(A \cap B)}{Pr(A)} \\
& = \frac{\frac{1}{3}}{\frac{1}{2}} \\
& = \frac{2}{3}
\end{align}
となります。\(Pr(B|A)\)が求まりました。
よって、
取り出した玉が赤い玉がであったという条件のもとで、数字が1である確率は\(\frac{2}{3}\)
であるとなります。
公式を使わなくても解けるけど?
この問題は公式を使わなくても感覚的に、
”取り出した玉が赤いときは、その数字が1である確率が\(\frac{2}{3}\)”
であることが分かったかもしれません。
確かに、この例題のように単純な問題は、感覚的に解くこともできます。
しかし、少し複雑な問題になると、感覚では解けなくなるので、この例題のような簡単な問題で条件付き確率の公式を使うことに慣れておくことが大切です。
ここで学んだ条件付き確率の詳しい解説は、以下のページで行っています。
不安な人は、一読しておきましょう。
乗法定理(じょうほうていり)
ベイズの定理への第一ステップは、上で解説した条件付き確率でした。
次に、第二ステップは”乗法定理”です。安心してください。まったく難しくありません。
これは、条件付き確率の式をちょっとだけ変形したものです。
ベイズの定理を構成する重要な要素となりますので、ここもしっかりと理解して先へ進みましょう。
復習ですが、条件付き確率の式は、
$$Pr(B|A) = \frac{Pr(A \cap B)}{Pr(A)}$$
と表現することができました。
この式は、
”事象Aが起こったという条件のともで、事象Bが起こる確率”
を表現しているのでしたね。
ここから両辺に\(Pr(A)\)を掛けて、以下のように式を変形しましょう。
$$Pr(A \cap B) = Pr(B|A) \times Pr(A)$$
※右辺と左辺を入れ替えています。
これが乗法定理です。
乗法定理のちょっとした性質
以上が乗法定理の式ですが、この式のちょっとした性質も知っておきましょう。
上の乗法定理の式は、事象Aと事象Bを入れ替えても何も問題ないはずです。ですので、
$$Pr(B \cap A) =Pr(A|B) \times Pr(B)$$
も成り立ちます。
ここでよく考えると、\(Pr(A \cap B)\)と\(Pr(B \cap A)\)はどちらも「事象Aと事象Bが同時に起こる確率」を表しているため、
$$Pr(A \cap B) = Pr(B \cap A)$$
ですね。よって、上記2式より、
$$Pr(A \cap B) =Pr(A|B) \times Pr(B)$$
が成り立ちます。これが紹介したかったちょっとした性質です。
要は、右辺のAとBを入れ替えても成り立ちますよ!ということです。
乗法定理は何を表しているのか?
$$Pr(A \cap B) = Pr(B|A) \times Pr(A)$$
は、何を表しているのでしょうか?それを少しだけ考えておきましょう。
それぞれの\(Pr\)は、
\begin{align}
Pr(A \cap B) & = \text{事象Aと事象Bが同時に起こる確率} \\
Pr(B|A) & = \text{事象Aが起こったという条件のもと、事象Bが起こる確率} \\
Pr(A) & = \text{事象Aが起こる確率} \\
\end{align}
です。
つまり、乗法定理は、
事象Aと事象Bが同時に起こる確率\(Pr(A \cap B)\)は、事象Aが起こったという条件のもと事象Bが起こる確率\(Pr(B|A)\)に事象Aが起こる確率\(Pr(A)\)を掛けたものである
ということです。

乗法定理を使った例題
以下は乗法定理を使った例題です。
袋の中に赤い玉と青い玉が三つずつ入っているとします。

ここから、Aさんが一つ玉を取り出します。玉の色を確認した後、その玉を袋に戻します。
次に、Bさんが同じように一つ玉を取り出します。
このとき、AさんもBさんも赤い玉を取り出す確率を求めましょう。
この問題を解いてみましょう。
乗法定理を考えます。
$$Pr(A \cap B) = Pr(B|A) \times Pr(A)$$
事象Aと事象Bを、
- 事象A:Aさんが赤い玉を取り出す
- 事象B:Bさんが赤い玉を取り出す
とすれば、\(Pr(A \cap B)\)は、
$$Pr(A \cap B) = \text{AさんとBさんがどちらも赤い玉を取り出す確率}$$
となります。これがいまの問題で求めたい答えそのものですね。
また、\(Pr(B|A)\)は、
$$Pr(B|A) = \text{Aさんが取り出したのは赤い玉だったという条件のもとBさんが赤い玉を取り出す確率}$$
です。
しかし、Aさんは取り出した玉を袋に戻すため、Bさんが赤い玉を取り出す確率はAさんの結果に左右されません。
※一方の結果に、もう一方の結果が左右されない(依存しない)ということを”独立である”と言います。いまの場合は、一度取り出した玉を袋の中に戻すため独立が成り立ちます。
なので、\(Pr(B|A)\)は単に、\(Pr(B)\)と同じことですので、
$$Pr(B|A) = Pr(B) = \frac{3}{6} = \frac{1}{2}$$
となります。
最後に、Aさんが赤い玉を取り出す確率\(Pr(A)\)も、
$$Pr(A) = \frac{3}{6} = \frac{1}{2}$$
ですので、これらを乗法定理に代入して、
$$Pr(A \cap B) = Pr(B|A) \times Pr(A) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$$
です。
よって、
$$\text{AさんとBさんがどちらも赤い玉を取り出す確率} = \frac{1}{4}$$
となります。
これが、乗法定理の使い方です。
スポンサーリンク
ベイズの定理の説明
いよいよ、ベイズの定理の説明です。
ベイズの定理の導出
まずは、ベイズの定理を導出してみましょう。
ここまでに学んできた式の整理します。
まず、第一ステップでは、条件付き確率の式を学びました。
$$Pr(B|A) = \frac{Pr(A \cap B)}{Pr(A)}$$
です。
それぞれの確率\(Pr\)の意味は、
\begin{align}
Pr(B|A) & = \text{事象Aが起こったという条件のもとで、事象Bが起こる確率} \\
Pr(A \cap B) & = \text{事象Aと事象Bが同時に起こる確率} \\
Pr(A) & = \text{事象Aが起こる確率}
\end{align}
ですね。
第二ステップでは、乗法定理を学びました。
この式は、条件付き確率の式を少し変形して、
$$Pr(A \cap B) = Pr(A|B) \times Pr(B)$$
と書けました。※AとBが入れ替わっても成り立つ「乗法定理のちょっとした性質」で導出した式となっていることに注意してください。
ここで、上式の乗法定理を条件付き確率の式に代入しましょう。すると、
$$Pr(B|A) = \frac{Pr(A|B) \times Pr(B)}{Pr(A)}$$
と書けます。
これがもっとも簡単なベイズの定理です。
一般的な定理への拡張
上の式は、もっとも簡単なベイズの定理でしたが、さらに一般的な形へ変形していきます。
まず、事象Bは事象Aが起こるという条件のもとで、複数の事象(\(B_1, B_2, B_3, \cdots\, B_k\))が起こる可能性があるとします。
これは、例えばサイコロを二回振ることを考えると理解できます。
サイコロを一回振って3の目が出た(事象A)という条件のもと、次にサイコロを振ったときに起こる事象Bは、サイコロの目が1,2,3,4,5,6の六パターンあり、複数事象あります。
※一回目に振ったサイコロは二回目のサイコロの目になんの影響も及ぼしません(すなわち独立です)。
なので、ここで複数の事象の中のある一つの事象という意味で、事象\(B\)を事象\(B_i\)とします。すると、上式は、
$$Pr(B_i|A) = \frac{Pr(A|B_i) \times Pr(B_i)}{Pr(A)}$$
と書けます。
さらに、右辺の分母\(Pr(A)\)は、
$$Pr(A) = Pr(A \cap B_1)+Pr(A \cap B_2)+ \cdots Pr(A \cap B_k)$$
と書けます。
事象\(A\)が起こる確率は、事象\(B_i\)が起こったという条件のもとで事象\(A\)が起こる確率をすべて足し合わせたものであるという式です(下のイメージ図)。
例えば、サイコロを考えます。
事象\(A\)を”1の目が出る確率”とすれば、確率\(Pr(A)\)は、
$$Pr(A) = \frac{1}{6}$$
というのは、すぐに分かるでしょう。
事象\(B_i\)はサイコロの場合、六パターンあり、
- \(B_1\):サイコロで一の目が出る確率
- \(B_2\):サイコロで二の目が出る確率
- \(B_3\):サイコロで三の目が出る確率
- \(B_4\):サイコロで四の目が出る確率
- \(B_5\):サイコロで五の目が出る確率
- \(B_6\):サイコロで六の目が出る確率
となります。
\(Pr(A \cap B_1)\)であれば、事象\(A\)と事象\(B_1\)が同時に起こる確率であり、この場合はどちらも一の目が出る確率となります。
よって、
$$Pr(A \cap B_1) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36}$$
となります。
これは、\(B_i\)の\(i=1,2,3,4,5,6\)についてすべて同じ確率ですので、
$$Pr(A \cap B_1)+Pr(A \cap B_2)+ \cdots Pr(A \cap B_6) = \frac{1}{36} \times 6 = \frac{1}{6}$$
ですね。
よって、
$$Pr(A) = Pr(A \cap B_1)+Pr(A \cap B_2)+ \cdots Pr(A \cap B_k)$$
が成り立つことが分かったと思います。
では、この\(Pr(A)\)を、
$$Pr(B_i|A) = \frac{Pr(A|B_i) \times Pr(B_i)}{Pr(A)}$$
に代入すると、
$$Pr(B_i|A) = \frac{Pr(A|B_i) \times Pr(B_i)}{Pr(A \cap B_1)+Pr(A \cap B_2)+ \cdots Pr(A \cap B_k)}$$
となり、さらに乗法定理(\(Pr(A \cap B_i) = Pr(B_i) Pr(A|B_i)\))を使うと、
$$Pr(B_i|A) = \frac{Pr(A|B_i) \times Pr(B_i)}{Pr(B_1) Pr(A|B_1)+Pr(B_2) Pr(A|B_2)+ \cdots Pr(B_k) Pr(A|B_k)}$$
です。
最後に、シグマ記号を使って表現すると、
$$Pr(B_i|A) = \frac{Pr(A|B_i) Pr(B_i)}{\sum_{j=1}^{k} Pr(A|B_j) Pr(B_j)}$$
となります。
これが一般的なベイズの定理です。
例題に挑戦しよう
公式だけではイメージが掴めません。最後に実際にベイズの定理を使ってみましょう。
以下の例題を解いてみましょう。
以下のように3つの箱の中に、当たりくじとはずれくじが入っています。
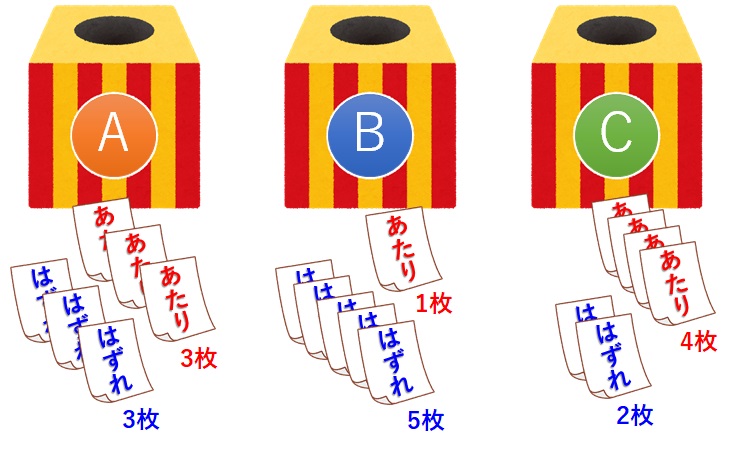
箱A、B、Cに入っているくじは、
- 箱A:あたりくじ3つ、はじれくじ3つ
- 箱B:あたりくじ1つ、はじれくじ5つ
- 箱C:あたりくじ4つ、はじれくじ2つ
です。
この箱の中からくじを一つ取り出したとき、そのくじは「あたり」でした。
ただし、このくじがどの箱から取り出されたものかは分かりません。
このとき、くじが箱Bから取り出された確率はいくらでしょうか?
まず、ベイズの定理を思い出しましょう。一般的な形は以下のような式でしたね。
$$Pr(B_i|A) = \frac{Pr(A|B_i) Pr(B_i)}{\sum_{j=1}^{k} Pr(A|B_j) Pr(B_j)}$$
この左辺\(Pr(B_i|A)\)は事象\(A\)が起こったという条件のもとで、事象\(B_i\)が起こる確率を表していますので、ここでは箱Bから取り出すということで\(i=2\)として、事象\(A\)と事象\(B_2\)は次のように設定しましょう。
- 事象\(A\):あたりくじが取り出された(結果)
- 事象\(B_2\):箱Bから取り出された(原因)
つまり、\(Pr(B_2|A)\)は、
取り出されたくじがあたりだったとき、そのくじが箱Bから取り出されたものである確率
ということになります。これを求めることが、例題を解くことになります。
次にベイズの定理の右辺ですが、事象\(B_j\)を袋\(j\)から玉を取り出すという行為に設定すると、いま袋は1,2,3の三つですので、\(j=1,2,3\)のみとなります。
よって、ベイズの定理は、
$$Pr(B_2|A) = \frac{Pr(A|B_2) Pr(B_2)}{Pr(A|B_1) Pr(B_1) + Pr(A|B_2) Pr(B_2) + Pr(A|B_3) Pr(B_3)}$$
となります。
まずは、右辺の\(Pr(B_1), Pr(B_2), Pr(B_3)\)を考えてみましょう。
これは、箱A、B、Cからくじが取り出された確率ですが、どの箱が選ばれるかはランダムと考えてよいので、
$$Pr(B_1)=Pr(B_2)=Pr(B_3)=\frac{1}{3}$$
とどの箱が選ばれたかという確率は平等として考えることが妥当です。
次に、\(Pr(A|B_1)\)ですが、これは事象\(B_1\)が起こった(箱Aからくじが取り出された)という条件のもと、事象Aが起こる(あたりくじが取り出される)確率です。
よって、箱Aに入っているあたりくじとはずれくじの数を考えると、
$$Pr(A|B_1) = \frac{3}{6} = \frac{1}{2}$$
です。
同様に、\(Pr(A|B_2)\)と\(Pr(A|B_3)\)は、
- \(Pr(A|B_2)\):箱Bから玉が取り出されたという条件のもと、あたりくじが取り出される確率
- \(Pr(A|B_3)\):箱Cから玉が取り出されたという条件のもと、あたりくじが取り出される確率
なので、
\begin{align}
Pr(A|B_2) & = \frac{1}{6}\\
Pr(A|B_3) & = \frac{4}{6} = \frac{2}{3}
\end{align}
です。
あとは、これらをベイズの定理に代入して、
\begin{align}
Pr(B_2|A) & = \frac{Pr(A|B_2) Pr(B_2)}{Pr(A|B_1) Pr(B_1) + Pr(A|B_2) Pr(B_2) + Pr(A|B_3) Pr(B_3)} \\
& = \frac{\frac{1}{6} \times \frac{1}{3}}{\frac{1}{2} \times \frac{1}{3} + \frac{1}{6} \times \frac{1}{3} + \frac{2}{3} \times \frac{1}{3}} \\
& = \frac{\frac{1}{18}}{\frac{3}{18}+\frac{1}{18}+\frac{4}{18}} \\
& = \frac{1}{8} \simeq 0.125 = 12.5\%
\end{align}
よって、取り出されたくじがあたりだったとき、そのくじが箱Bから取り出された確率は\(12.5\%\)となります。
どうでしょうか?自分の感覚と比べてベイズの定理から導かれた答えは妥当ですか?
まとめ
- ベイズの定理とは、既に起こったことからその原因の確率を求める手法である
- 以下のことをまず理解しよう
- 条件付き確率
- 乗法定理
- この二つの公式からベイズの基本公式が導かれる
- ベイズの定理に慣れるためには、例題にたくさん触れておくことが大切です
ここでは、くじ引きという例題を解いてみましたが、ベイズの定理を使った例題として有名なものに病気の確率を推測するというものがあります。
この例では自分の感覚と全く違う答えがベイズの定理によって明らかになります。面白いですので、ぜひご覧ください↓

























ディスカッション
コメント一覧
ベイズは、とても面白いですね。
本で知りました♪
本の内容と、同じように説明されていて、分かりやすかったです♪
ようやくわかりました。