【中学2年数学（確率）】赤い玉や白い玉など色付きの玉を使った確率の問題の解き方

2018年4月14日2018年6月11日

赤い玉や白い玉など色付きの玉を取り出す確率の問題

赤い玉や白い玉など色付きの玉が使われた確率の問題は、

袋や箱に入ったこれらの玉を取り出していき、取り出した玉の色がある条件になるときの確率を求めさせる問題

となっています。

このページでは、このような色付き玉が登場する確率問題を解くコツや重要なポイントを紹介しましょう。

実際に問題を解きながら、コツや重要ポイントを説明していくので、ゆっくりと理解しながら進めていってくださいね。

 

わからないところがあれば、下のコメント欄で質問も受け付けていますので、気軽に聞いてくださいね。

では、はじめていきましょう。

 

スポンサーリンク

色付き玉の問題は”くじ”の問題の発展バージョン

色付き玉を袋から取り出していく問題と同じような確率の問題に、”くじ”を使った問題があります。

くじを使った問題も、袋の中から”くじ”を取り出すという同じような操作を行いますが、

くじは”アタリ”と”ハズレ”の二種類しかない

のにたいして、色付き玉の問題は、

いろいろな色の玉が登場し、二種類以上の玉が使える

という違いがあります。

 

すなわち、色付き玉の問題はくじの問題の発展バージョンということができます。

 

よって、重要なポイントなども共通している部分が多く、少し簡単な”くじの問題”を先にマスターしておくと、ここで学ぶ色付き玉の問題がスムーズに理解できるでしょう。

まず、くじの問題についての重要ポイントやコツを知っておきたいという方は、以下のページをはじめに読んでみましょう。

それから、このページに戻ってきてくださいね。

 

では、実際に問題を解いていきながら、色付き玉の確率問題をマスターしていきましょう。

 

問題を解いてみよう

まずは、以下の問題を一緒にやってみましょう。

 

問題①の解き方

まずは、問題①から解いていきましょう。

2回袋から玉を取り出しますが、このとき赤い玉と白い玉が1個ずつになる場合は、

• 1回目に赤い玉を取り出し、2回目に白い玉を取り出す
• 1回目に白い玉を取り出し、2回目に赤い玉を取り出す

のどちらかです。

このそれぞれの場合について、そのようになる確率を求め、最後に足すことで答えが求まります。

 

1回目に赤い玉を取り出し、2回目に白い玉を取り出す

まずは、1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率を求めましょう。

1回目に赤い玉を取り出す確率はどうなったでしょうか？

全部で6個ある玉の中で、赤い玉は2個です。

よって、

$$\text{1回目に赤い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

ですね。

 

次に、2回目に白い玉を取り出す確率です。

2回目に袋から玉を取り出すとき、問題文から「1回目に取り出した玉は袋の中に戻す」とありますので、袋の状態は1回目に引いたときとまったく同じです。

よって、全部で6個ある玉の中で、白い玉は2個ですので、

$$\text{2回目に白い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

ですね。

 

最後に、1回目と2回目の確率を掛けると、1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率が求まります。

$$\text{1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率} = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}$$

 

まだ終わりではありません。

取り出した玉が赤い玉と白い玉である場合は、取り出す順番が逆の、1回目に白い玉を取り出し、2回目に赤い玉が取り出す場合があります。

次はその場合についても同じように考えましょう。

1回目に白い玉を取り出し、2回目に赤い玉を取り出す

この場合も玉の色が変わっただけで、上と同じように計算できます。

1回目に白い玉を取り出す確率は、全部で6個ある玉の中で、白い玉は2個ですので、

$$\text{1回目に白い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

です。

 

続いて、2回目に赤い玉を取り出す確率は、全部で6個ある玉の中で、赤い玉は2個ですので、

$$\text{2回目に赤い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

です。

 

最後に、これらの確率を掛けると、1回目に白い玉を取り出し、2回目に赤い玉を取り出す確率が求まります。

$$\text{1回目に白い玉を取り出し、2回目に赤い玉を取り出す確率} = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}$$

となります。

最後にすべての場合についての確率を足す

これで、2回袋から玉を取り出すとき、赤い玉と白い玉が1個ずつになるパターンである

• 1回目に赤い玉を取り出し、2回目に白い玉を取り出す
• 1回目に白い玉を取り出し、2回目に赤い玉を取り出す

の確率をそれぞれ求めることができました。

 

それは、

• \( \text{1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率} = \frac{1}{9} \)
• \( \text{1回目に白い玉を取り出し、2回目に赤い玉を取り出す確率} = \frac{1}{9} \)

です。

これを足して、2回袋から玉を取り出すとき、赤い玉と白い玉が1個ずつになる確率を求めると、

\begin{align}
\frac{1}{9} + \frac{1}{9} = \frac{2}{9}
\end{align}

となり、これが最終的な答えです。

 

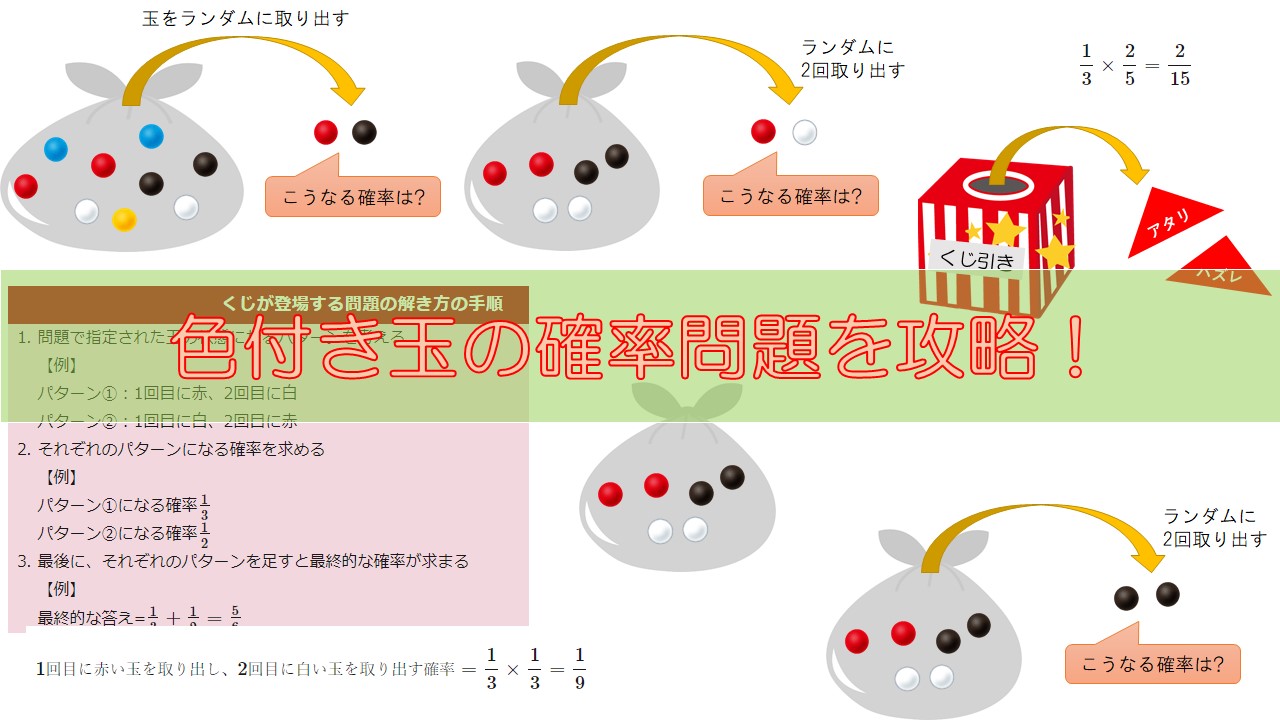
ここで、問題を解く手順を復習しておきましょう。

基本的には、この手順にそって解いていけばどんな問題でも解けるようになっています。

問題②の解き方

次に問題②を解いていきましょう。

問題を思い出しましょう。

でしたね。

この問題も何も特別なことはありません。

上で説明した解き方の手順にそって進めていけばよいです。

 

まずは、どちらとも黒い玉を取り出すパターンを考えます。

このパターンは、

• 1回目に黒い玉を取り出し、2回目も黒いを取り出す

です。

問題①は2つのパターンがありましたが、問題②では1パターンだけです。

 

次に、このパターンになる確率を求めます。

1回目に袋から黒い玉を取り出す確率は、全部で6個ある玉の中で、黒い玉は2個ですので、

$$\text{1回目に黒い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

です。

 

また、1回目に取り出した玉は袋に戻すため、2回目も袋の状態は変わらないです。

ですので、2回目に袋から黒い玉を取り出す確率も、

$$\text{2回目に黒い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

です。

 

最後に、これらを掛けて、

$$\text{1回目に黒い玉を取り出し、2回目も黒いを取り出す確率} = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}$$

となります。

 

今回はこの1パターンだけでしたので、これで終了です。

よって、2回袋から玉を取り出したとき、どちらとも黒い玉である確率は、

$$\text{2回袋から玉を取り出したとき、どちらとも黒い玉である確率} = \frac{1}{9}$$

となります。

 

問題①の”赤い玉と白い玉が1個ずつになる確率”は\(\frac{2}{9}\)でしたので、どちらの玉とも黒い確率は、その半分の確率であるということがわかりましたね。

どうですか？あなたの感覚と一致していましたか？

 

ここまでの重要なポイントは、解き方の手順です。

基本的な解き方はすべて一緒ですので、必ずここで覚えておきましょう。

 

スポンサーリンク

袋に玉を戻さない場合はどうなる？

次は、以下のような問題に挑戦してみましょう。

前に見た問題とほとんど同じですね。

違うところは、

1回目で取り出した玉を袋に戻さない

という点です。

ここに注意して解いていきましょう。

 

問題①の解き方

解き方は、これまでと同じです。

まず、どのような取り出し方をしたときに、”取り出した2つの玉が赤い玉1個、白い玉1個となる”かを考えていきます。

これは以下の2つのパターンが考えられますね。

• 1回目に赤い玉を取り出し、2回目に白い玉を取り出す
• 1回目に白い玉を取り出し、2回目に赤い玉を取り出す

 

1回目に赤い玉を取り出し、2回目に白い玉を取り出すパターン

一つ目のパターンから考えていきます。

1回目は、6個の玉から2個ある赤い玉を取り出すため、確率は、

$$\text{1回目に赤い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

です。

 

続いて、2回目には、白い玉を取り出す確率でが、ここで注意すべきは、

1回目に取り出した玉は、袋には戻さない

ということです。

つまり、1回目に取り出した赤い玉はもう袋にはありません。

なので、全部で5個の玉の中から2個の白い玉を取り出す確率を考えることになります。

$$\text{2回目に白い玉を取り出す確率} = \frac{2}{5}$$

 

最後に、二つの確率を掛けて、”1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率”を求めると、

$$\text{1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率} = \frac{1}{3} \times \frac{2}{5} = \frac{2}{15}$$

となります。

 

まだ終わりではないですよ。

もう一つのパターンの確率も考える必要があります。

 

1回目に白い玉を取り出し、2回目に赤い玉を取り出すパターン

次は、1回目に白い玉を取り出し、2回目に赤い玉を取り出すパターンの確率です。

これも同じです。

1回目は、6個の玉から2個ある白い玉を取り出すため、確率は、

$$\text{1回目に白い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

です。

 

また、2回目は白い玉が1個減っている袋から、赤い玉を取り出す確率です。

5個の玉から2個ある赤い玉を取り出すため、確率は、

$$\text{2回目に赤い玉を取り出す確率} = \frac{2}{5}$$

です。

 

よって、これら二つの確率を掛けて、”1回目に白い玉を取り出し、2回目に赤い玉を取り出す確率”を求めると、

$$\text{1回目に白い玉を取り出し、2回目に赤い玉を取り出す確率} = \frac{1}{3} \times \frac{2}{5} = \frac{2}{15}$$

となります。

 

最後にすべての場合についての確率を足す

そして、最後に、すべてのパターン（ここでは、上で求めた以下の2つ）の確率

• \(\text{1回目に赤い玉を取り出し、2回目に白い玉を取り出す確率} = \frac{2}{15}\)
• \(\text{1回目に白い玉を取り出し、2回目に赤い玉を取り出す確率} = \frac{2}{15}\)

を足すと、”取り出した2つの玉が赤い玉1個、白い玉1個となる”確率が求まります。

$$\text{取り出した2つの玉が赤い玉1個、白い玉1個となる確率} = \frac{2}{15} + \frac{2}{15} =\frac{4}{15}$$

よって、問題①の答えは、\(\frac{4}{15}\)です。

 

ここで、1回目の玉を取り出した後、袋に戻す場合と戻さない場合のときの確率の違いをみてみましょう。

両方の計算結果は、以下のようになりました。

\begin{align}
\text{1回目の玉を取り出した後、袋に戻す場合} = \frac{2}{9} = 22.22\% \\
\text{1回目の玉を取り出した後、袋に戻さない場合} = \frac{4}{15} = 26.66\%
\end{align}

わずかに、袋に戻さない方が、問題の条件を満たす確率が高くなっていることがわかります。

 

問題②の解き方

続いて、問題②の両方黒い玉になる確率です。

解き方は、まったく同じなので、途中の計算は省略気味で進めます。

 

まず、両方の玉が黒になるパターンは、

• 1回目で黒い玉を取り出し、2回目も黒い玉を取り出す場合

の1パターンしかありません。

 

1回目は6個の玉から2個の黒い玉を取り出すので、

$$\text{1回目で黒い玉を取り出す確率} = \frac{2}{6} = \frac{1}{3}$$

ですね。

 

次の2回目は、袋には全部で5個の玉しかなく、その中に黒い玉は1個だけです。

よって、

$$\text{2回目で黒い玉を取り出す確率} = \frac{1}{5}$$

です。

 

最後にこれらの確率を掛けて、”両方の玉が黒になる”確率を求めると、

$$\text{両方の玉が黒になる確率} = \frac{1}{3} \times \frac{1}{5} = \frac{1}{15}$$

です。

よって、問題②の答えは、\(\frac{1}{15}\)となります。

 

では、袋に玉を戻さない場合の確率と比べてみましょう。

それぞれは、以下のような確率になります。

\begin{align}
\text{1回目の玉を取り出した後、袋に戻す場合} = \frac{1}{9} = 11.11\% \\
\text{1回目の玉を取り出した後、袋に戻さない場合} = \frac{1}{15} = 6.66\%
\end{align}

玉を戻さない場合の方が、かなり低い確率になってしまいましたね。

 

問題①でみた”赤い玉と白い玉を取り出す確率”の場合は、ここまでの差は出なかったのですが、今回は、倍近くの差が出ました。

問題の条件によって、玉を戻すか戻さないかで差の大きさが違うのは面白いですね。

 

まとめ

お疲れさまでした。

色付きの玉が登場する確率の問題は、ここでの内容が理解できればあとは、応用問題を解いていくことで、どんな問題も解けるようになりますよ。

もしわからないことがあったら、以下のコメント欄から気軽に聞いてくださいね。

 

では、色付き玉の確率問題について、重要ポイントをおさらいして終わりましょう。

では、また会いましょうね。