【中学2年数学(確率)】区別して確率問題を解く理由 – なぜ区別しないとダメなのか?

- 確率で”区別して考える”がイマイチわからない
- なぜ区別して考えないといけないかを知りたい
- 確率の問題でよく同じ間違いをしてしまう
確率の問題ではよく、”区別して考えなさい”と言われます。
そんなとき、「区別って?」や「区別しないとなんでいけないの?」と思ったことはありませんか?
ここでは、そんな方の悩みを解決するためのページです。
【動画解説】
※記事の内容はもっと詳しい説明となっていますので、記事にも目を通してみてくださいね。
確率問題を区別して解くとは
よく確率を勉強していると、”区別して考える”という言葉が登場します。
まずはじめに、”区別する”とはどのような意味なのかを復習しておきましょう。
例題を使って説明します。
例えば、次のような問題が出題されたとします。
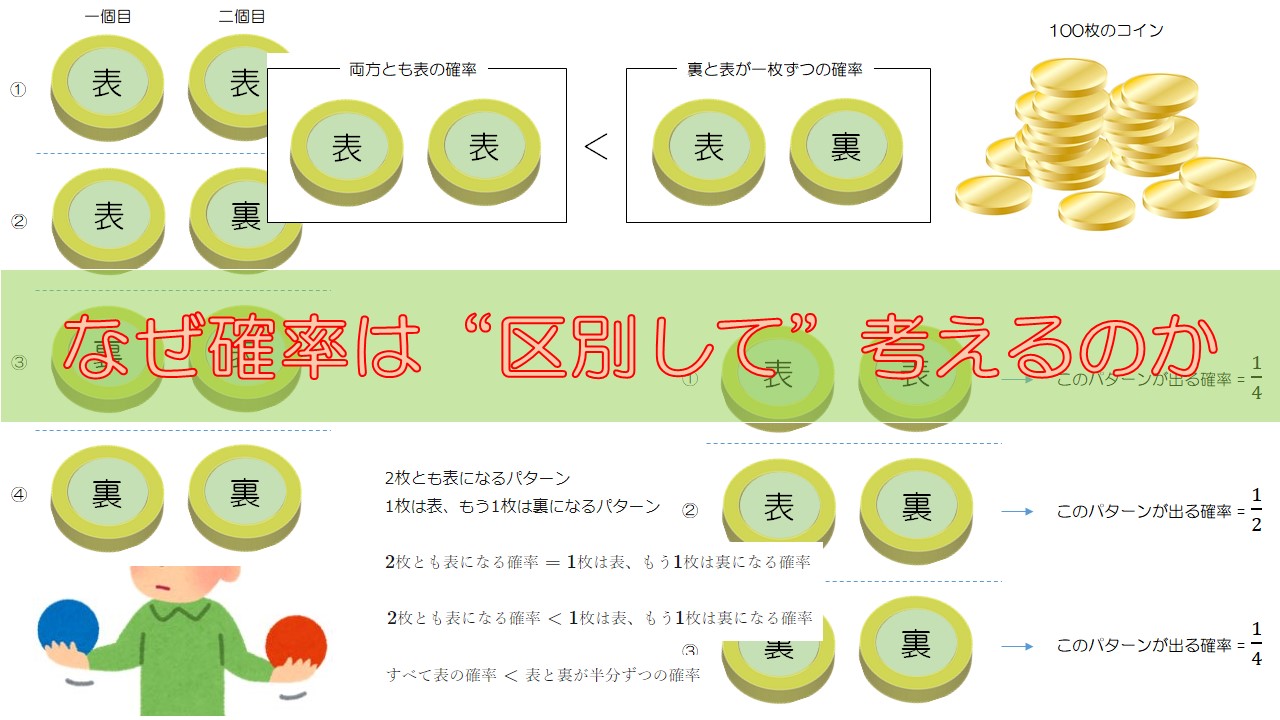
2枚のコインを同時に投げて、両方とも裏である確率を求めなさい
この問題を2枚のコインを区別して考えた場合と、区別しないで考えた場合の両方について見ていきましょう。
区別して考える
まずは、コインを区別して考える場合を説明します。
このとき、コインの裏表のすべてのパターンを描くと、
となります。
コインを区別しているので、コインに”1個目”と”2個目”というふうに名前を付けました。
このように、2つのコインに別の名前をつけて区別しているのですね。
②と③は表と裏が1枚ずつですが、1個目が表の場合と、2個目が表の場合では違うパターンとして扱います。
すべてのパターンは全部で4通りですね。
さて、問題は両方とも裏である確率を求めることです。
この4通りの中で、二つのコインが裏のパターンは④の1通りだけですね。
なので、
$$\text{2枚のコインを投げて、両方とも裏である確率} = \frac{1}{4}$$
となります。
これが正解の答えです。
区別しないで考える
次に、コインを区別しないで考える場合はどうなるでしょうか?
このとき、コインの裏表のパターンは、
のようになります。
コインを区別していないので、1枚のコインが表で、もう1枚のコインが裏であれば、それで1パターンとしています。
なので、表が1つと裏が1つである②のパターンは1つしかないのです。
よって、すべての場合の数は3通りとなります。
これより、答えは、
$$\text{2枚のコインを投げて、両方とも裏である確率} = \frac{1}{3}$$
となります。
しかし、この答えは間違っています。
それは、①や③が出る確率がそれぞれ\(\frac{1}{4}\)なのに対して、②が出る確率は\(\frac{1}{2}\)と①~③では出る確率が違っているからです。
\begin{align}
\text{①のパターンになる確率} = \frac{1}{4} \\
\text{②のパターンになる確率} = \frac{1}{2} \\
\text{③のパターンになる確率} = \frac{1}{4}
\end{align}

パターン分けして、場合の数から確率を求めるときは、すべてのパターンで出る確率が同じでなければいけません。
”すべてのパターンで出る確率が同じ”であることを確率の分野では「同様に確からしい」というのですが、授業などで聞いたことはありませんか。
確率の問題は、この「同様に確からしい」条件のもとで考えないといけません。
でも、なぜ②のパターンだけ出る確率が違うのでしょうか?
「②のパターンだけ出る確率が他のパターンよりも高いと言われても、感覚的にわからないよ」
と思うかもしれません。
わたしがそうでしたので。
以下では、
「②のパターンが出る確率が高いのはなぜ?」
「なぜ区別しないで出した答えは間違っているの?」
を納得してもらうために、様々な考え方を紹介します。
スポンサーリンク
たくさんのコインがあると考える方法
上で述べたような理由を感覚的に理解するために、多くの参考書やサイトで、
”たくさんのコインがあると考えてみるとよい”
とあります。
例えば、上で紹介した問題は、コインが2枚でした。
このコインを100枚にして考えてみるのです。

この100枚のコインを一斉に振った時、すべてが表になる確率はどのくらいでしょう?
すぐにはわかりませんが、か~なり低いことは想像できますよね。
次は、100枚のコインのうち、半分の50枚が表、残り50枚が裏になる確率を想像してみましょう。
こちらは、ちょうど半分半分でコインの表と裏が出る確率は、低いでしょう。
しかし、すべてのコインが表になる確率よりも高いと感じませんか?
つまり、100枚のコインを振ったとき、
$$\text{すべて表の確率} < \text{表と裏が半分ずつの確率}$$
ということになります。
このことはコインが100枚でなくとも、成り立つはずです。
なので、コインが2枚のときでも、
$$\text{すべて表の確率} < \text{表と裏が半分ずつの確率}$$
が成り立つとすれば、

上の図のようになり、確率が違うことが納得できるのではないでしょうか?
なので、
となるのですね。
ここまで読んで納得した人は、ラッキーです。
しかし、まだまだ納得できない人もいることでしょう。
そんな人は、次の説明を用意してあります。
連続でコインを振ると考える

上の図が納得できない人へ続いての説明です。
コインを2枚に戻しましょう。問題を思いだすと、
2枚のコインを同時に投げて、両方とも裏である確率を求めなさい
でした。
ここで、問題はコインを同時に振るとなっていますが、連続で振ると考えます。
連続で振っても、同時に振っても結果は変わらないはずです。
実際、コインを同時に振っても、どちらかがわずかに早く表か裏が決まりますよね。
ぴったり同時にコインが止まることの方が珍しいです。
これは、連続で振っているのと同じことです。
さて、コインを連続で振ると決めて、
- 2枚とも表になるパターン
- 1枚は表、もう1枚は裏になるパターン
のどちらの確率が大きくなるかを考えます。
まずは1枚目を振ります。
その結果が、表だったとします。
このとき、”2枚とも表になるパターン”と”1枚は表、もう1枚は裏になるパターン”のどちらの可能性も残っていますね。
続いて、2枚目を振り表であれば”2枚とも表”になりますし、裏になれば”1枚は表、もう1枚は裏”になります。
つまり、1枚目を振って表だったときは、
$$\text{2枚とも表になる確率} = \text{1枚は表、もう1枚は裏になる確率}$$
となるのです。
では、1枚目を振って裏だった場合はどうでしょうか?
このとき、”2枚とも表になるパターン”は、この時点で可能性が無くなりました。
一方、”1枚は表、もう1枚は裏になるパターン”はまだ可能性が残っています。
2枚目のコインが表であれば、”1枚は表、もう1枚は裏になるパターン”になれるのです。
よって、1枚目を振って裏だったときは、
$$\text{2枚とも表になる確率} < \text{1枚は表、もう1枚は裏になる確率}$$
となるのです。
トータルで考えると、
$$\text{2枚とも表になる確率} < \text{1枚は表、もう1枚は裏になる確率}$$

であることがわかりますね。
スポンサーリンク
まとめ
どうでしたでしょうか?
ここでわかって欲しかったのは、確率の問題ではなぜコインやサイコロなどを”区別する”必要があるかどうかでした。
区別しないと、それぞれのパターンが出る確率が変わってしまうからですね。
まだよくわからなかった人は、時間をおいてもう一度読み返してみてください。
きっといつかわかる日が来ます!勉強なんてそんなもんです。
質問もお待ちしていますので、下のコメントにメッセージを送ってくださいね。
では、このページの重要ポイントをまとめて終わりましょう。
確率の問題は、コインやサイコロ、くじや玉などは、基本的に、区別して考えること!
区別するとは、それぞれに名前を付けて違うものとして考えることです。
区別しないといけない理由は、区別しなかったら
それぞれのパターンになる確率が違ってくるから
です。
確率の問題は、どのパターンも同じ確率で起こる状況で考えないといけません。
これを”同様に確からしい”といいます。
では、また会いましょう。

】カードが登場する確率の問題の解き方-100x100.jpg)






















ディスカッション
コメント一覧
コイントスの確率の説明方法、どれもわかりやすいと感じました。先生は独立事象の確率計算に「区別できない」という考えを持ち込むと論理的な矛盾が生じてしまうことをご存知でしょうか。
例えば、2個のサイコロを投げて、①両方とも偶数になる確率②片方が偶数で片方が奇数になる確率③両方とも奇数になる確率
を考えてみて下さい。
【区別できるサイコロ】
偶奇だけ考えた場合の数①1通り②2通り③1通り
そこで確率は①1/4②1/2③1/4
目まで考えた場合の数①9通り②18通り③9通り
やはり確率は①1/4②1/2③1/4で合理性あり。
【区別できないサイコロ】
偶奇だけ考えた場合の数①1通り②1通り③1通り
そこで確率は①1/3②1/3③1/3
目まで考えた場合の数①6通り②9通り③6通り
確率は①2/7②3/7③2/7と矛盾した結果になって
しまいます。
これを生徒に教える必要はないと思いますが、教える側は知っておいた方が良いのではないでしょうか。
是非、先生に広めて頂きたいと思います。
よろしくお願いします。