【中学2年数学(確率)】”少なくとも”が出てくる確率の問題を攻略しよう

- 数学の確率で”少なくとも”が出てくる問題がわからない
- ”少なくとも”の問題の解き方やコツを詳しく解説して欲しい
- どんな問題があるのかを知りたい
このページでは、確率の問題で”少なくとも”という表現が出てきたときの解き方を丁寧に解説しています。
一見、難しそうな”少なくとも”の問題ですが、解き方がわかれば普通の問題よりも簡単にすばやく解けるようになります。
では、実際に問題を解きながら、コツや重要ポイントをみていきましょう。
”少なくとも”は問題を簡単に解けるチャンス
確率の問題では、よく
”少なくとも”
という表現が登場します。
この表現が登場したとき、普通どおりに確率の問題を解くと、すごく大変になる場合が多いです。
そのため解くのに時間がかかり、複雑な計算をしないといけないようになるのでミスも増えてしまいます。
それが、出題者の狙いです。意地悪ですね。
そんな”少なくとも”が登場する問題ですが、逆に問題を簡単に解くチャンスでもあります。
とても簡単に解ける方法が存在するからです。
これを知っていると、問題を解く時間の短縮になりますし、計算量が少なくなるためミスも減るでしょう。
ここでは、その方法を詳しく説明しましょう。
必ず、テストで役に立つはずですよ。
スポンサーリンク
”少なくとも”が出てくる問題ってどんな問題?
まずは、”少なくとも”という表現が出てくる問題はどんなものなのかを確認しておきましょう。
例えば、以下のような問題です。
4つのコインがあります。

この4つのコインを投げて、少なくとも1つが表(おもて)である確率を求めなさい。
問題文に”少なくとも”が登場していますね。
”少なくとも1つが表である場合”
というのは、
- ”表が1つの場合”
- ”表が2つの場合”
- ”表が3つの場合”
- ”表が4つの場合”
とたくさんのパターンがありますね。

全部で4パターンあります。
普通に解いてみる
まずは、普通に解いてみましょう。
上で示したように、表が1つ、2つ、3つ、4つの場合について、それぞれの場合の数を求め、最後にすべてを足せばよいですね。
まずは、表が1つ場合から考えましょう。
表は1つだけ出る場合は以下の4通りあります。
次に、2枚表が出る場合は、

この6通りです。
続いて、3枚表が出る場合は、
4通りです。
最後に4枚表の場合は、すべてが表の場合の1通りですね。

よって、”少なくとも表が出る場合の数”は、これらを全部足して、
$$\text{少なくとも表が出る場合の数} = 4+6+4+1 = 15$$
となり、15通りとなります。
ここで、確率の公式を思い出しましょう。
確率の公式は、
$$\text{確率} = \frac{\text{ある条件が起こる場合の数}}{\text{すべての場合の数}}$$
でした。
いまの問題の場合は、”ある条件”とは、”少なくとも1枚が表である”ということです。
\begin{align}
\text{確率} & = \frac{\text{ある条件が起こる場合の数}}{\text{すべての場合の数}} \\
& = \frac{\text{少なくとも1枚が表である場合の数}}{\text{すべての場合の数}}
\end{align}
さっき”少なくとも1枚が表である場合の数”は15通りと求めたので、あとは”すべての場合の数”を求めればよいですね。
コインを\(n\)枚投げたときのすべての場合の数は、
$$\text{コインを\(n\)枚投げたときのすべての場合の数} = 2^n$$
で求めることができます。
コインを使った確率の問題に関しては、
をご覧ください。
よって、いまの場合、コインは4枚なので”すべての場合の数”は、
$$\text{”すべての場合の数”} = 2^4 = 16$$
となり、16通りです。
あとは、確率の公式を使って、
\begin{align}
\text{確率} & = \frac{\text{少なくとも1枚が表である場合の数}}{\text{すべての場合の数}} \\
& = \frac{15}{16}
\end{align}
となり、4枚のコインを投げたとき、少なくとも1枚が表である確率は\(\frac{15}{16}\)となります。
どうでしたか?
解けないことはないですが、答えにたどり着くまでにかなり時間がかかってしまいました。
この原因は、表が1枚の場合、表が2枚の場合、表が3枚の場合、表が4枚の場合、と4つの場合をそれぞれ考えなければいけなかったためです。
これは、問題文に”少なくとも”という表現が登場していたからなのです。
次に、この問題をもっと簡単に解く方法を紹介しましょう。
”少なくとも”が出たらこう解こう
もう一度、問題を確認しましょう。
4つのコインがあります。

この4つのコインを投げて、少なくとも1つが表(おもて)である確率を求めなさい。
でしたね。
少なくとも1枚が表ということは、そうではない場合はすべてのコインが裏の場合であるということがわかります。
なので、ここでは最初に、すべてのコインが裏の場合の確率について考えていきましょう。
確率の公式で表現すると、
\begin{align}
\text{すべてのコインが裏の確率} & = \frac{\text{すべてのコインが裏の場合の数}}{\text{すべての場合の数}}
\end{align}
”すべてのコインが裏の場合の数”はすぐにわかります。

それは、1通りだけです。
”すべての場合の数”は、すでに普通どおりの方法のときに求めました。
$$\text{”すべての場合の数”} = 2^4 = 16$$
となり、16通りです。
よって、すべてのコインが裏の場合の確率は、
\begin{align}
\text{すべてのコインが裏の確率} & = \frac{\text{すべてのコインが裏の場合の数}}{\text{すべての場合の数}} \\
& = \frac{1}{16}
\end{align}
ですね。
では、問題の”少なくとも1枚が表の確率”はどうなるでしょうか?
それは、”すべてが裏の場合の確率”の残りの確率となります。
すべてが裏でなければ、少なくとも1つは表のはずですからね。
残りの確率は、その確率を\(1\)から引けば求まります。
よって、
$$\text{少なくとも1枚が表の確率} = 1 – \frac{1}{16} =\frac{15}{16}$$
となります。
この方法であれば、答えを簡単にすばやく求めることができましたね。
”少なくとも”の問題を解く方法を復習すると、
- ”少なくともある条件になる確率”は、それ以外になる確率を求める
- 最後に\(1\)からその確率を引く
という手順です。
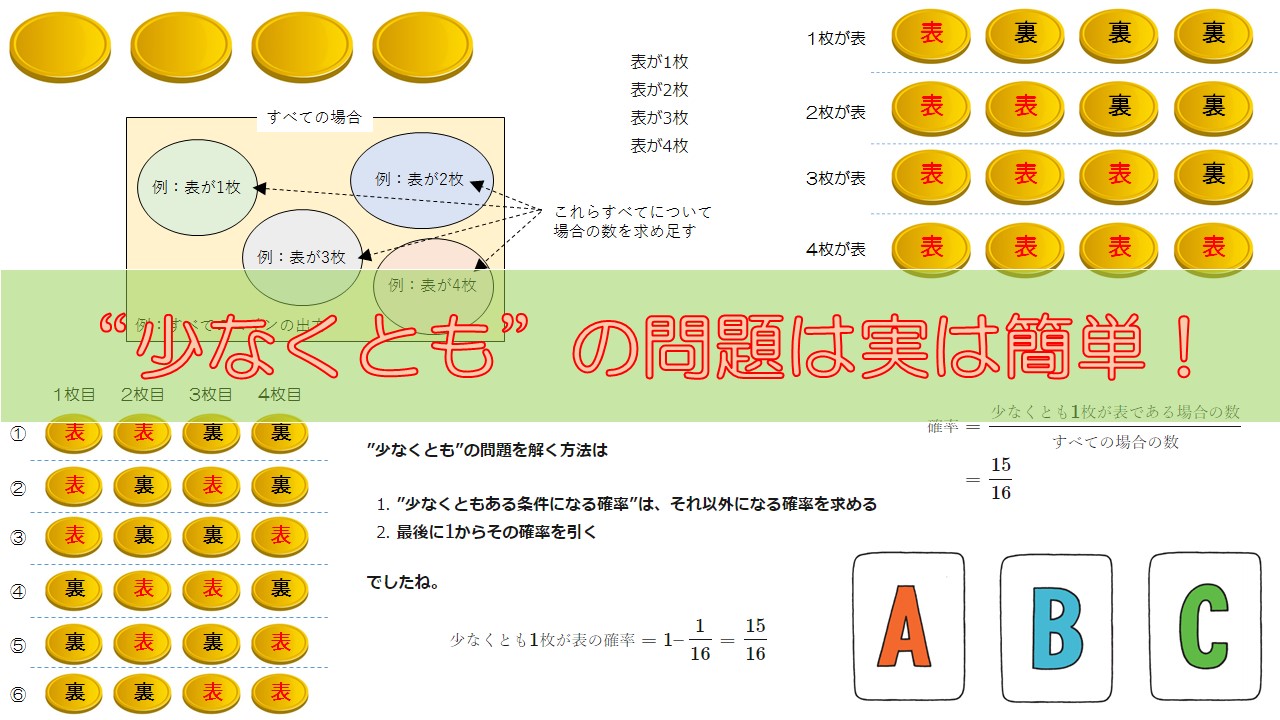
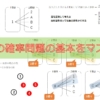
”少なくとも”を図でイメージする
”少なくとも”の問題をイメージしましょう。
下の図を見てください。

ある行為を行ったとき、起こるすべての場合を黄色い領域で表現しました。
上の問題でいうと、”すべてのコインの出方”にあたります。
このうち、”少なくとも”という表現で表せる部分は、下の図のようにたくさんパターンがあるのです。
上の問題でいうと、”少なくとも表が1枚でる場合”は、
- 表が1枚
- 表が2枚
- 表が3枚
- 表が4枚
の4パターンありましたね。
普通の方法だと、これら全部について、それぞれ場合の数を求めて足すからメンドくさいのです。
一方、2番目に説明した”少なくとも”の問題を解く特別な方法は、黄色い領域の場合の数だけを求めます。
そして、最後の”すべての場合の数”からそれを引くことで、青や緑のすべての円の領域を足したものが求まるのです。
この方法であれば、どんなに多くのパターンが存在しても、場合の数を求めるのは1回でいいのです。
スポンサーリンク
練習してみよう
では、”少なくとも”が登場する問題を練習してみましょう。
以下の問題に挑戦してみてください。
もちろん解答は下に詳しく説明しているので、解き終わったり、分からなくなったり、解くのがメンドイときに見てくださいね。
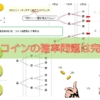
A,B,Cと描かれた3枚のカードがあります。

ここから、1枚カード引いてカードを戻さずに、もう1回カードを引くとき、
少なくとも1枚がAである確率を求めなさい。
では、解いてみましょう。
”少なくとも”の問題を解く方法は
- ”少なくともある条件になる確率”は、それ以外になる確率を求める
- 最後に\(1\)からその確率を引く
でしたね。
まずは、”少なくとも1枚がA”である場合以外(つまり、1枚もAがない)には、どんな場合があるかを考えましょう。
それは、
- 1回目がBで、2回目がC
- 1回目がCで、2回目がB
の2通りだけです。
また、すべての場合の数は、1回目は3枚のカードから1枚を選び、2回目は2枚のカードから1枚を選ぶため、
$$\text{すべての場合の数} = 3 \times 2 = 6$$
となり、\(6\)通りです。
よって、確率の公式にこれらを代入して、
\begin{align}
\text{少なくとも1枚がAである以外の確率} = \frac{2}{6}
\end{align}
です。
最後に、これを\(1\)から引けば、”少なくとも1枚がAである確率”が求まります。
\begin{align}
\text{少なくとも1枚がAである確率} = 1 – \frac{2}{6} = \frac{2}{3}
\end{align}
となります。
どうでしたか?
うまく解けたでしょうか?
まとめ
お疲れさまでした。
問題に”少なくとも”という表現がでてきたら、出題者としては、ここで紹介した方法を使ってといてねという考えがあると考えてまず間違いないです。
では、最後に重要なポイントを復習して終わりにしましょう。
問題文に”少なくとも”という表現が出てきたら、
- ”少なくともある条件になる確率”は、それ以外になる確率を求める
- 最後に\(1\)からその確率を引く
という手順で解くことで、計算を簡単にでき、ミスも減ります。
計算が楽になる理由は、たくさんのパターンを一つ一つ計算しないでよくなるためです。
では、確率の計算を楽しんでくださいね。

























ディスカッション
コメント一覧
確率は苦手で混乱しているのですが、「少なくともの練習問題」の回答についてです。
1-2/6=1/3
の回答は間違いでしょうか?
匿名さん、これ、間違いですよね。
僕も自分の答えが間違っているかと思って何度も計算してしまいました。
管理人です。
お二人とも、混乱させて申し訳ないです。
修正しました。
間違いを指摘してくれてありがとうございます。
よく分かりました!
【一枚だけが出る場合】と指定されたタイプと
【少なくとも◯◯出る場合】のタイプの問題で
混乱していましたが、余剰の法則のようなもので、
1からマイナスすれば良いんですね!
確率は割合で、%でもあるから、
1ってことは100%ってことですよね。
そこから引き算すればよいわけですね!
簡単な例題のおかげで考え方がわかりましたし、
問題に【少なくとも】と書いてある場合は、かえって簡単になる!と説明されていたお陰でよくわかるようになりました!
混乱も無くなりそうだと思いました!!
根本原理が大切ですね!
根本原理を何度も繰り返してマスターしてないと、
必ず混乱するからもっと繰り返してから読み進めないとダメだと思いました。
日本の教科書とか先生って根本原理の重要性をもっともっと繰り返しアピールしないと、【最後の最後までわかってない子】が増えちゃうような気がしますね。