【中学2年数学（確率）】コインを使った確率の問題を攻略しよう

2018年4月10日2019年10月5日

【動画解説】
※記事の内容はもっと詳しい説明となっていますので、記事にも目を通してみてくださいね。

コインを使った確率の問題を攻略しよう

ここは、中学数学の確率のなかでもコインが登場する問題を攻略するためのページです。

 

コインを使ったいろんな問題が出てくるので、一つ一つ理解しながら進めましょう。

間違いやすい部分や、注意する点も丁寧に説明しています。

 

このページを読み終わったときには、あなたはコインの確率問題の大半を解けるようになっているでしょう。

 

確率の公式を確認

問題に入る前に、確率の公式について確認しておきましょう。

確率は、

$$\text{確率} = \frac{\text{ある条件が起こる場合の数}}{\text{すべての場合の数}}$$

で求めることができましたね。

この公式は、常に頭の中に入れていおいてください。

 

上の公式から場合の数を求めることが、確率を求めることにつながることがわかります。

「場合の数ってなんだったっけ？」

という人は、まずは以下のページから読んでみてくださいね。

 

では、はじめましょう。

スポンサーリンク

2枚のコインを同時に投げる場合

問題

この問題を解いてみましょう。

解き方のヒントは、すべてのコインの組み合わせを描いて”2枚とも表が出る場合の数”と”すべての場合の数”を求めることです。

 

解答

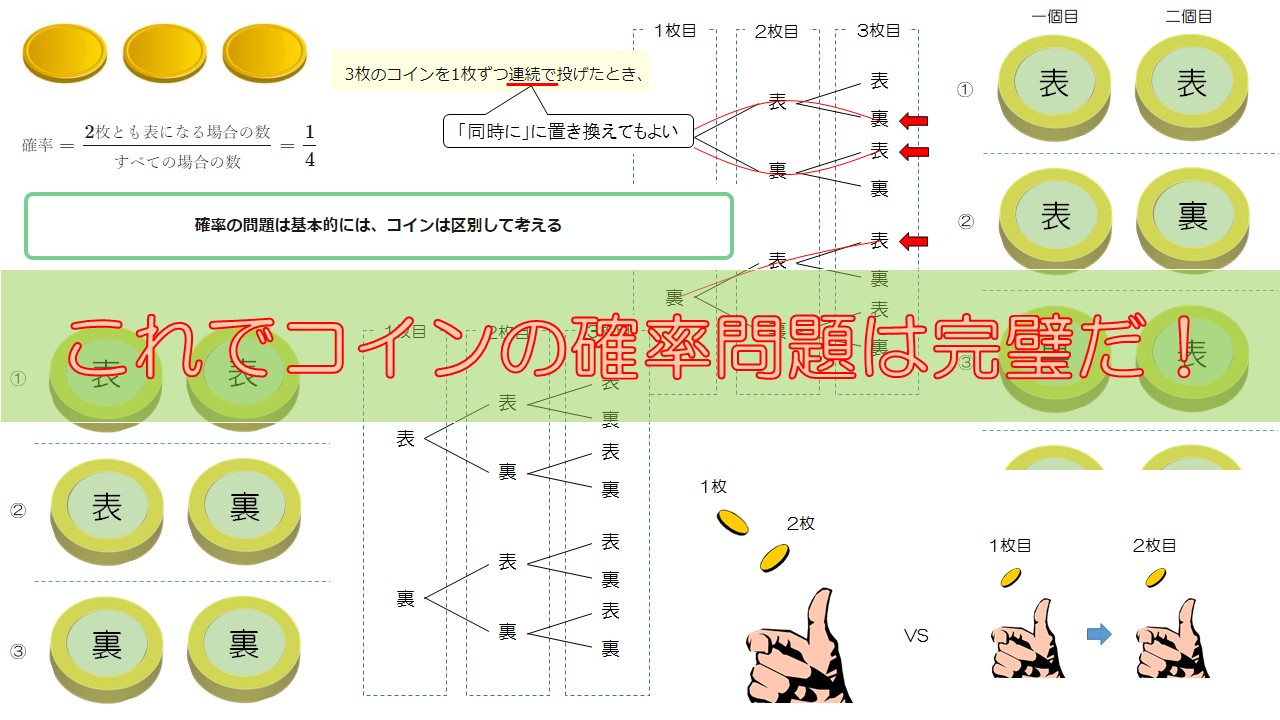
確率の基本は、すべての組み合わせのパターンを描くことです。

描いてみましょう。すると、

となりますね。

これより、すべての場合の数は4通りあることがわかります。

 

ここで注意点です。

上の図で、コインを”一個目”と”二個目”というふうに、名前をつけて区別して考えていることに注意です。

区別しないで考えた場合の答えを、後からお見せしますが、区別しないで考えると間違えてしまいます。

 

問題は、「2枚とも表が出る場合の確率を求めよ」となっています。

この中で2つのコインがどちらとも表となるパターンは何通りあるでしょう。

これは、①の1通りだけですね。

よって、確率の公式にこれらを代入すると、

$$\text{確率} = \frac{\text{2枚とも表になる場合の数}}{\text{すべての場合の数}} = \frac{1}{4}$$

となり、答えは\(\frac{1}{4}\)です。

 

間違った解答

確率の問題でよく間違えるのが、コインを区別しないで考えてしまうことです。

コインを区別しないで考えると、裏と表のパターンを、

• 両方、表の場合
• 一方が表で、もう一方が裏の場合
• 両方、裏の場合

という3パターンに考えてしまいます。

 

そして、両方表の場合は1通りなので、答えを、

$$\text{確率} = \frac{\text{2枚とも表になる場合の数}}{\text{すべての場合の数}} = \frac{1}{3}$$

としてしまうと、これは間違いです。

 

コインを区別しないと、なぜ間違えてしまうのでしょうか？

 

それには、以下のページをご覧ください。

ここでは、

確率の問題は基本的には、コインは区別して考える

と覚えておきましょう。

 

これは、コインでなくとも、サイコロでも、くじ引きでも、同じです。

区別して考えましょう。

 

3枚のコインを同時に投げる場合

問題

次は、コインが3枚に増えましたね。

 

解答

解き方は前回と基本的に同じです。

まずは、すべてのパターンを書き出します。

 

ただし、今回は樹形図を使って解いてみましょう。

樹形図とは、

こんなヤツです。

樹形図について、「知らない」という方は、まずは、以下のページから樹形図を学びましょう。

 

もちろん、樹形図を使わず、すべてのパターンを書きだして解くこともできますが、パターン数が多くなるときは、樹形図が便利です。

 

では、3枚のコインについて、樹形図を描いてみましょう。

全部で8パターンの組み合わせがあることがわかります。

よって、すべての場合の数は8通りです。

 

次に、この中から表が2枚と裏が1枚のパターンは何通りあるかを確認します。

すると、

このように3通りであることがわかります。

 

よって、確率の公式により、

$$\text{確率} = \frac{\text{表が2枚と裏が1枚になる場合の数}}{\text{すべての場合の数}} = \frac{3}{8}$$

となり、3枚のコインを同時に投げたとき、表が2枚と裏が1枚のパターンが出る確率は\(\frac{3}{8}\)です。

 

樹形図を使ってコインの問題を解けるようになりましょうね。

 

スポンサーリンク

同時ではなく1枚ずつ投げた場合

ここまでは順調ですか？

では、次の問題はどうでしょうか。

さっきの問題とほとんど同じです。

違う点は、先ほどの問題は”コインを同時に投げる”でしたが、今回は”コインを連続で投げる”に変わっています。

 

では、解き方は何か変わるでしょうか？

実は、コインを同時に投げる場合も連続で投げる場合も解き方は変わりません。

 

それは、どちらの場合も、一方のコインの結果がもう一方のコインの結果に影響しないからです。

例えば、

「連続でコインを投げる場合、はじめに投げた方のコインが”表”だったからといって、2投目のコインは”裏”が出やすい」

というようなことはありませんよね。

 

連続で投げる場合は、投げた人が片方のコインの結果をもう片方より早く知ることができるということです。

 

しかし、よく考えてみるとコインを同時に投げる場合も、ぴったりと同時にコインの結果が出るわけではありませんよね。

一瞬はやく、どちらかのコインの結果が決まるはずです。

ただ、その結果をコインを投げた人は確認する間もなく、2枚目のコインの結果が決まるというだけです。

 

なので、実質的にとコインを同時に投げる場合も連続で投げる場合も同じなのです。

なので、もう答えをいう必要はないですね。

 

ここで、知ってもらいたかったのは、コインの確率の問題で、

「同時に」と「連続に」

といった問題文が出てきたときは、この二つは同じなので、どちらか好きな方に置き換えて解いてもオッケーだということです。

 

まとめ

お疲れ様でした。

このページでは、コインを使った確率の問題の解き方のコツを紹介してきました。

ここまで理解できた人は、コインの確率の問題は怖くありませんよ。

 

確率が苦手は人は、少しでも確率がわかるようになってくれていれば、うれしいです。

 

それでは、最後に重要ポイントをまとめて終わりましょう。

では、さようなら～。