【中学1年数学(正の数・負の数)】分数の足し算・引き算の解き方 – ”分数とは何か”からはじめよう

- 分数の足し算・引き算が苦手
- 分数の計算で何からやっていいか混乱する
- 負の数の分数が登場する計算を克服したい
分数は小学校で登場しますが、わかりづらい単元です。
ここでは、分数の意味をイメージでしっかりと理解したあとに、分数の正の数と負の数の足し算と引き算を説明していきます。
特に、混乱を招くのが、負の数を用いた分数の引き算になります。
なので、ここでは負の数の分数を克服するための考え方を丁寧に説明します。
分数とはなんだろう
前回は、正の数・負の数を使った足し算と引き算について説明しました。
分数ではなく、整数の正の数・負の数がわからない人は、下のページから読んでみてください。
今回は分数の計算で、正負の数が登場します。
ところで、「分数とはなんだろう?」と悩んだことはありませんか?
分ける数と書いて、分数(ぶんすう)というものは、いったいどのようなものなのでしょうか?
分数は、数学の勉強の中だけで登場するのもではありません。
分数は日常生活で登場するものです。
例えば、アメが10個あって、これをAさんとBさんとCさんの3人で分け合ったとします。
Aさんが3個、Bさんが3個、Cさんが4個で分け合ったとします。
これを分数で表すと、次の通りになります。
- Aさん…\(10\)個の中の\(3\)個のアメだから\(\frac{3}{10}\)
- Bさん…\(10\)個の中の\(3\)個のアメだから\(\frac{3}{10}\)
- Cさん…\(10\)個の中の\(4\)個のアメだから\(\frac{4}{10}\)
分数で考えることのメリット
分数の意味を具体的な例を使って、詳しく確認してみましょう。
まずは、分数を使わない場合の例です。
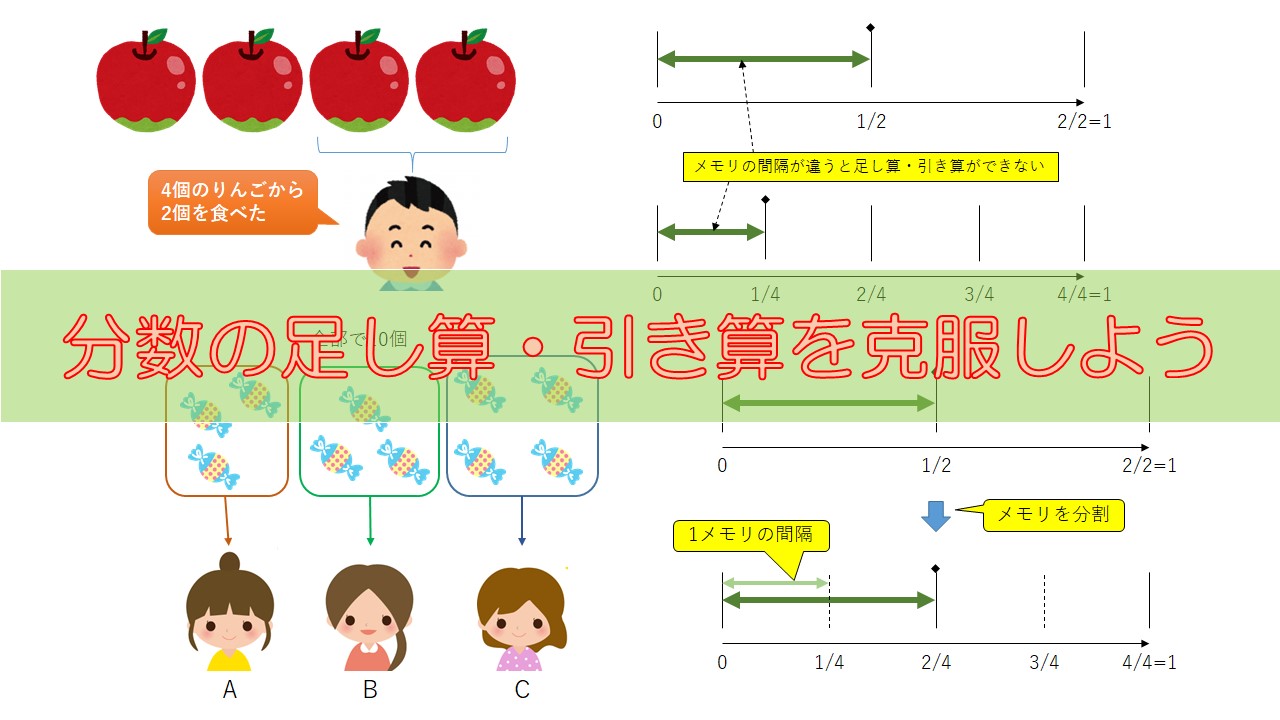
りんごが4個あって、2個のりんごを食べたので、今は残りが2個あります。

この場合の数学的な表現方法は、どのような方法が考えられるでしょうか?
例えば、何個のりんごが残っているか計算する方法は、次の通りになります。
$$\text{残りのりんご} = 4 − 2 = 2$$
この例のように、残りのりんごの計算結果である2個のみの情報を教えてもらっても、全体が何個であったかなどの情報が分からないと思いませんか?
では、次に分数を使った表現方法を考えてみましょう。
上の例で残りのりんごを分数で表現すると、
$$\frac{\text{残りのりんごの数}}{\text{全てのりんごの数}} = \frac{2}{4}$$
となります。
このように\(\frac{2}{3}\)と分数で表現すると全体がいくつで、残りがいくつという情報が含まれるのです。
そのために、例①にくらべて例②の方の情報が増えていることが分かります。
このように、
分数とは、全体と”部分(残り)”を表すこと
というのが基本的な考え方になります。
分数は、りんごが全体で幾つあるか、そして、残りが幾つあるかを表しているのです。
スポンサーリンク
分数の数学的な意味
話を戻して、分数の意味をもう少し数学的に考えてみましょう。
実は、分数の数学的な表現である\(\frac{2}{4}\)の”―”は、実は割り算の意味と同じになります。
つまり”―”を\(\div\)と置き換えて計算してよいということです。
$$2 \div 4 = 0.5$$
計算結果はこのようになりますね。
一方、分数の表現の\(\frac{2}{4}\)を約分すると
$$\frac{2}{4} = \frac{1}{2}$$
となります。
この\(\frac{1}{2}\)は、2個の中の1個なの半分を意味します。
つまり、半分の意味ですね。
先ほど計算した割り算の結果は、\(0.5\)でした。
これも半分の意味になりますね。
割り算で計算した場合も、分数で考えた場合もどちらも”半分”という答えが出ましたね。
このように割り算と分数の答えは、実は同じ意味を表しているのです。
通分
分数の意味が理解できたところで、このページのメインである”分数の足し算・引き算”を学んでいきましょう。
ただし、その前に分数の足し算・引き算に絶対に必要な通分(つうぶん)についてはじめに説明します。
まずは通分の意味を理解しよう
分数を計算する時には、約分と通分というルールが必要です。
今回の計算では、全ての問題で通分という計算が必要になります。
その理由は、分数は全体の数である分母を揃えない計算ができないからです。
この理由を別な視点から見てイメージしていきましょう。
例えば、
$$\frac{1}{2} + \frac{1}{4}$$
の計算で、通分する前の定規の目盛りは、それぞれ\(\frac{1}{2}\)と\(\frac{1}{4}\)であり下図の通りです。
メモリの間隔がズレていることが分かります。
このように、メモリの間隔がズレていると足し算や引き算はできません(※掛け算や割り算はできます)。
計算するためには、このメモリの間隔を合わせないといけないことが分かりました。
メモリの間隔を合わせるにはどうしたらよいでしょうか?
それは、長い間隔の方のメモリを細かい間隔のメモリに合うように分割してあげればよいでしょう。
つまり、いまの場合は\(\frac{1}{2}\)のメモリを\(\frac{1}{4}\)のメモリの間隔に合うように分割します。
上の図のように\(\frac{1}{2}\)のメモリをさらに半分にして、\(\frac{1}{4}\)メモリにしました。
このメモリで元々の\(\frac{1}{2}\)を表現すると、\(\frac{2}{4}\)ですね。
$$\frac{1}{2} = \frac{2}{4}$$
これが通分です。
通分とは、目盛りの間隔を揃える計算をしているですね。
スポンサーリンク
分数の足し算・引き算
これで、分数の足し算と引き算をする準備ができましたので、計算方法を学んでいきましょう。
ある数字\(X\)と数字\(Y\)がある時に、足し算と引き算を次の通りに書いてみます。
- 足し算:\(X+Y=Z\)
- 引き算:\(X-Y=Z\)
この\(X\)と\(Y\)に分数で表現される数字を当てはめてみます。
まず、\(X\)として、\(\frac{1}{2}\),\(-\frac{1}{2}\)を当てはめます。
\(Y\)として、\(\frac{1}{4}\)と\(-\frac{1}{4}\)を割り当てます。
分数の足し算
足し算から見ていきましょう。
このとき、足す数と足される数の符号を考えて、すべての計算パターンを書くと、
\begin{align}
& \frac{1}{2} + \frac{1}{4} \\
& -\frac{1}{2} + \frac{1}{4} \\
& \frac{1}{2} + \left(-\frac{1}{4} \right) \\
& -\frac{1}{2} + \left(-\frac{1}{4} \right)
\end{align}
の4パターンになります。
一つずつ丁寧に計算方法をみてきます。
\(\frac{1}{2} + \frac{1}{4}\)
$$\frac{1}{2} + \frac{1}{4}$$
を解いてみましょう。
まず、通分をします。分母の大きい方に合わせます。
分母が大きいということは、メモリの間隔が細かいということですね。

よって、
\begin{align}
\frac{1}{2} + \frac{1}{4} = \frac{2}{4} + \frac{1}{4}
\end{align}
となります。
通分の手順は、大きい方の数字に合わせる方法、分母同士の掛け算した数2×4で8を分母にする方法、最大公約数(これは別の単元で詳しく説明しますのでキーワードを頭においておきましょう)を分母にする方法などがありますが、ここでは大きい方の数字に合わせる方法を使いました。
これで分母が揃った(メモリが揃った)ので、分子同士を足し算することが可能になります。
これを解くと、
\begin{align}
\frac{1}{2} + \frac{1}{4} & = \frac{2}{4} + \frac{1}{4} \\
& = \frac{2+1}{4} \\
& = \frac{3}{4}
\end{align}
となります。答えは\(\frac{3}{4}\)、もしくは\(3 \div 4 = 0.75\)ですね。
\(-\frac{1}{2} + \frac{1}{4}\)
続いては、
$$-\frac{1}{2} + \frac{1}{4}$$
にチャレンジしましょう。
この問題も通分が必要になります。通分をすると次の通りになります。
\begin{align}
-\frac{1}{2} + \frac{1}{4} = -\frac{2}{4} + \frac{1}{4}
\end{align}
通分ができたの分子同士を足し算することができます。
最終的な結果は、次の通りになります。
\begin{align}
-\frac{1}{2} + \frac{1}{4} & = -\frac{2}{4} + \frac{1}{4} \\
& = \frac{-2+1}{4} \\
& = \frac{-1}{4} \\
& = -\frac{1}{4}
\end{align}
答えは、\(-\frac{1}{4}\)です。もしくは、\(-1 \div 4 = -0.25\)になります。
\(\frac{1}{2} + \left( -\frac{1}{4} \right)\)
同じようにして、
$$\frac{1}{2} + \left( -\frac{1}{4} \right)$$
も解いてみましょう。
まずは通分して、
\begin{align}
\frac{1}{2} + \left( -\frac{1}{4} \right) = \frac{2}{4} + \left( -\frac{1}{4} \right)
\end{align}
ですね。
この問題はカッコがついていますので、ここでカッコを外します。
すると、
\begin{align}
\frac{1}{2} + \left( -\frac{1}{4} \right) & = \frac{2}{4} + \left( -\frac{1}{4} \right) \\
& = \frac{2}{4} – \frac{1}{4}
\end{align}
となりますので、これを計算して、
\begin{align}
\frac{2}{4} – \frac{1}{4} & = \frac{2-1}{4} \\
& = \frac{1}{4} \\
\end{align}
です。答えは\(\frac{1}{4}\)、もしくは\(1 \div 4 = 0.25\)です。
\(-\frac{1}{2} + \left( -\frac{1}{4} \right)\)
最後は、
$$-\frac{1}{2} + \left( -\frac{1}{4} \right)$$
ですね。
これも今までと同じです。
通分をして、かっこを外し計算しましょう。
\begin{align}
-\frac{1}{2} + \left( -\frac{1}{4} \right) & = -\frac{2}{4} + \left( -\frac{1}{4} \right) \\
& = -\frac{2}{4} – \frac{1}{4} \\
& = \frac{-2-1}{4} \\
& = \frac{-3}{4} \\
& = -\frac{3}{4}
\end{align}
よって答えは、\(-\frac{3}{4}\)もしくは、\(-3 \div 4 = -0.75\)となります。
分数の引き算
次は引き算を見ていきましょう。
基本的に計算方法は同じです。
まずは、通分をして、かっこがあれば外して計算すればオッケーです。
引き算は以下の4つのパターンがありますね。
\begin{align}
& \frac{1}{2} – \frac{1}{4} \\
& -\frac{1}{2} – \frac{1}{4} \\
& \frac{1}{2} – \left(-\frac{1}{4} \right) \\
& -\frac{1}{2} – \left(-\frac{1}{4} \right)
& \end{align}
一つずつ見ていきましょう。
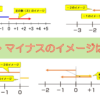
引き算は、”数字のマイナスの符号”、そして”引き算の記号としてのマイナス”があるのでこの2つのマイナスを混乱しないようにいて下さい。
マイナスについては、以下のページを見ると「マイナスとはなんなのか?」というイメージがつくと思います。
\(\frac{1}{2} – \frac{1}{4}\)
では、まずは、
$$\frac{1}{2} – \frac{1}{4}$$
から解いていきましょう。
まずは、通分ですね。その後に分子同士を計算します。
\begin{align}
\frac{1}{2} – \frac{1}{4} & = \frac{2}{4} – \frac{1}{4} \\
& = \frac{2 – 1}{4} \\
& = \frac{1}{4}
\end{align}
よって、答えは\(\frac{1}{4}\)となります。もしくは、\(1 \div 4 = 0.25\)ですね。
\(-\frac{1}{2} – \frac{1}{4}\)
次は、
$$-\frac{1}{2} – \frac{1}{4}$$
です。
先ほどとまったく同じ方法で解きます。
通分して、分子を計算できるようにしましょう。
\begin{align}
– \frac{1}{2} – \frac{1}{4} & = – \frac{2}{4} – \frac{1}{4} \\
& = \frac{- 2 – 1}{4} \\
& = \frac{-3}{4} \\
& = – \frac{3}{4}
\end{align}
よって、答えは\(-\frac{3}{4}\)となります。もしくは、\(-3 \div 4 = -0.75\)ですね。
\(\frac{1}{2} – \left( -\frac{1}{4} \right)\)
次は、
$$\frac{1}{2} – \left( -\frac{1}{4} \right)$$
です。
今度は( )がついていますね。
まずは、通分しましょう。
\begin{align}
\frac{1}{2} – \left( -\frac{1}{4} \right) = \frac{2}{4} – \left( -\frac{1}{4} \right)
\end{align}
次にかっこを取りましょう。
\begin{align}
\frac{1}{2} – \left( -\frac{1}{4} \right) & = \frac{2}{4} + \frac{1}{4} \\
& = \frac{2 + 1}{4} \\
& = \frac{3}{4}
\end{align}
よって、答えは\(\frac{3}{4}\)です。もしくは、\(3 \div 4 = 0.75\)ですね。
\(-\frac{1}{2} – \left(-\frac{1}{4} \right)\)
最後は、
$$-\frac{1}{2} – \left(-\frac{1}{4} \right)$$
です。
まずは、通分しましょう。
\begin{align}
– \frac{1}{2} – \left( -\frac{1}{4} \right) = – \frac{2}{4} – \left( -\frac{1}{4} \right)
\end{align}
次にかっこを取りましょう。
\begin{align}
– \frac{1}{2} – \left( -\frac{1}{4} \right) & = – \frac{2}{4} + \frac{1}{4} \\
& = \frac{-2 + 1}{4} \\
& = \frac{-1}{4} \\
& = -\frac{1}{4}
\end{align}
よって、答えは\(-\frac{1}{4}\)です。もしくは、\(-1 \div 4 = -0.25\)ですね。
いかがでしたでしょうか?
分数の復習から入って、正負の分数の数の正負の足し算と引き算の計算が分かりましたか?
分数でも小数でも整数でも、考え方は、正負の数の足し算と引き算の計算方法は共通になります。
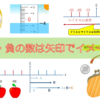
ここでは、数字を矢印に置き換えて計算したように、自分の中で計算のイメージをもつようにするとどんな問題でもよく考えれば解き方が思い浮かぶようになります。
ここではたくさんの具体的な数字で、正の数と負の数の分数の足し算と引き算をみてきました。
難しい部分もありますが、一つ一つ落ち着いて図をみながら確認をしていきましょう。
また、迷ったときは教科書に書いてある正負の数の分数の足し算と引き算のルール(公式)を確認しすることも問題解決に役に立つときもありますよ。
まとめ
分数の復習からはじめて、正負の数の足し算と引き算を説明してきました。
分数や小数や整数など表現方法が異なっていても、正負の数の足し算と引き算のルールは、同じであることが分かりました。
では、以下に重要なポイントをまとめて終わりましょう。
分数の足し算と引き算は、通分の考え方が大切です。
通分はめもりの間隔(あいだ)をそろえることで足し算・引き算ができるようになります。
分数でも小数でも整数でも正負の数の足し算と引き算のルールは共通です。計算式を頭でイメージすることがどんな問題も解けるようになることのポイントです。
正の数・負の数のイメージが湧かない人は、「【中学1年数学(正の数・負の数)】プラスとマイナスの計算の意味 – 足し算と引き算はこう考えよう」を参考にしてみてください。



























ディスカッション
コメント一覧
間違ってるよ
現中一です。予習のためにこのサイトを使用させてもらいましたが、このアホでもよくわかりました!
日本語が理解できてないのは俺だけ?